Алгоритм BFS для взвешенных графов - найти кратчайшее расстояние

Question

Я видел довольно много постов (а именно post1, post2, post3) на эту тему, но ни один из постов не предоставляет алгоритм для резервного копирования соответствующих запросов. Следовательно, я не уверен, что приму ответы на эти посты.

Здесь я представляю основанный на BFS алгоритм кратчайшего пути (с одним источником), который работает для неотрицательного взвешенного графа. Может ли кто-нибудь помочь мне понять, почему BFS (в свете алгоритма, основанного ниже BFS) не используются для таких задач (в том числе взвешенного графика)!

Алгоритм:

SingleSourceShortestPath (G, w, s):
    //G is graph, w is weight function, s is source vertex
    //assume each vertex has 'col' (color), 'd' (distance), and 'p' (predecessor) 
        properties

    Initialize all vertext's color to WHITE, distance to INFINITY (or a large number
        larger than any edge's weight, and predecessor to NIL
    Q:= initialize an empty queue

    s.d=0
    s.col=GREY     //invariant, only GREY vertex goes inside the Q
    Q.enqueue(s)  //enqueue 's' to Q

    while Q is not empty
        u = Q.dequeue()   //dequeue in FIFO manner
        for each vertex v in adj[u]  //adj[u] provides adjacency list of u
             if v is WHITE or GREY       //candidate for distance update
                  if u.d + w(u,v) < v.d        //w(u,v) gives weight of the 
                                               //edge from u to v
                      v.d=u.d + w(u,v)
                      v.p=u
                      if v is WHITE
                          v.col=GREY    //invariant, only GREY in Q
                          Q.enqueue(v)
                      end-if
                  end-if
              end-if
         end-for
         u.col=BLACK  //invariant, don't update any field of BLACK vertex.
                      // i.e. 'd' field is sealed 
    end-while

Время выполнения: насколько я вижу, это O(|V| + |E|), включая стоимость инициализации

Если этот алгоритм похож на любой существующий, пожалуйста, дайте мне знать

Answer 1

Поскольку псевдокод является алгоритмом Дейкста с очередью FIFO вместо очереди приоритетов, которая всегда сортируется на основе расстояний. Важный инвариант, что каждая посещенная (черная) вершина имеет вычисленное кратчайшее возможное расстояние, не обязательно будет истинной. И именно поэтому приоритетная очередь является обязательной для вычисления расстояния в (положительно) взвешенных графах.

Вы можете использовать свой алгоритм для невзвешенных графиков или сделать его не взвешенным, заменив каждое ребро весом n с n-1 вершины, соединенные ребрами с весом 1.

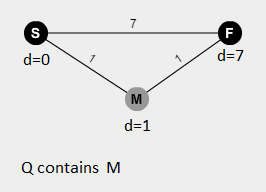
контрпример:

Состояние вычисления после первого Q.enqueue(s):

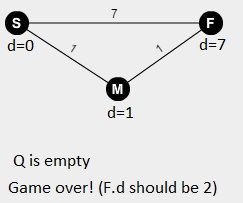
С вершины F сначала снимается с u = Q.dequeue() (в отличие от того, когда используется очередь с приоритетом расстояния), эта итерация не будет обновлять расстояние, F станет черным и инвариант будет нарушен.

Состояние вычисления после последней итерации:

Answer 2

Раньше у меня было такое же замешательство. Проверьте алгоритм SPFA. Когда автор опубликовал этот алгоритм в 1994 году, он утверждал, что он имеет лучшую производительность, чем Дейкстра со сложностью O(E), что неверно.

Вы можете рассматривать этот алгоритм как вариацию / улучшение Беллмана-Форда. В худшем случае сложность по-прежнему равна O(VE), поскольку один узел можно добавлять / удалять из очереди несколько раз. Но для случайного разреженного графика он определенно превосходит оригинальный Bellman-Ford, поскольку пропускает множество ненужных расслабляющих шагов.

Хотя это название "SPFA", кажется, не очень принято в научных кругах, после публикации оно стало очень популярным среди студентов ACM из-за его простоты и легкости реализации. Производительность мудрый Дейкстра является предпочтительным.

Answer 3

Похоже, вы реализовали классический алгоритм Дейкстры без кучи. Вы проходите матрицу через каждое ребро, а затем смотрите, сможете ли вы улучшить расстояние.

Answer 4

Обычно люди говорят, что это BFS, когда нет веса края.

• BFS: граф с постоянным весом ребер.

• Дейкстра: граф с весами ребер (может обрабатывать некоторые отрицательные ребра, если у
  него нет отрицательного цикла)

• Беллман-Форд и SPFA: график с отрицательным циклом.

Ваш код Dijkastra или SPFA вариант, а не простой BFS (хотя IS базируется на основе BFS alrorithm)