Как получить стандартное отклонение с помощью PyKalman?
Имея данные одномерного измерения, я хотел бы знать стандартные стандартные отклонения в каждой точке, используя фильтр Калмана. Моя процедура заключается в следующем:
from pykalman import KalmanFilter
import numpy as np
measurements = np.asarray([2, 1, 3, 6, 3, 2, 7, 3, 4, 4, 5, 1, 10, 3, 1, 5])
kf = KalmanFilter(transition_matrices=[1],
observation_matrices=[1],
initial_state_mean=measurements[0],
initial_state_covariance=1,
observation_covariance=1,
transition_covariance=0.01)
state_means, state_covariances = kf.filter(measurements)
state_std = np.sqrt(state_covariances[:,0])
print state_std
Это приводит к следующему странному результату:
[[ 0.70710678]
[ 0.5811612 ]
[ 0.50795838]
[ 0.4597499 ]
[ 0.42573145]
[ 0.40067908]
[ 0.38170166]
[ 0.36704314]
[ 0.35556214]
[ 0.34647811]
[ 0.33923608]
[ 0.33342945]
[ 0.32875331]
[ 0.32497478]
[ 0.32191347]
[ 0.31942809]]
Я ожидаю увеличения дисперсии для последних точек данных. Что я делаю неправильно?
1 ответ
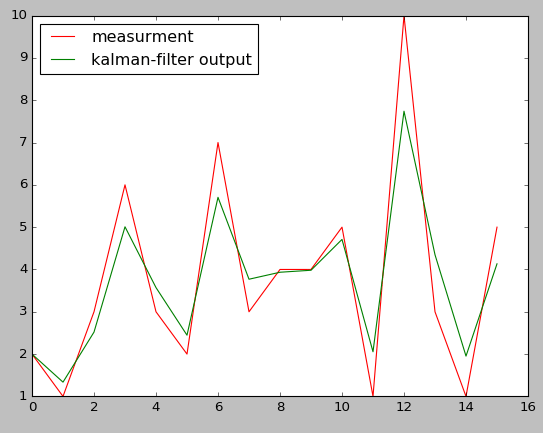
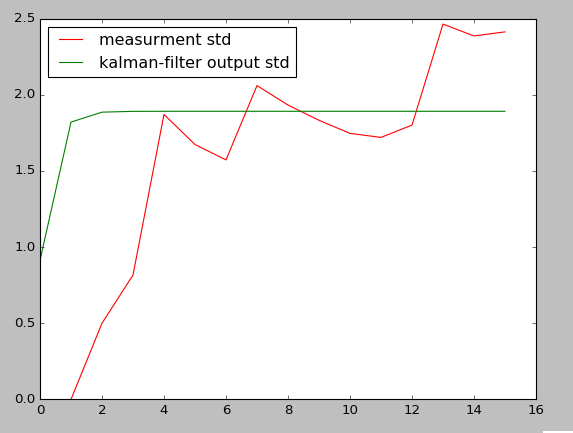
Поскольку все ковариационные матрицы (измерения, переходы), которые вы предоставили, малы (что означает, что вы не ожидаете такой большой неопределенности в наблюдениях), ковариация состояний не отражает вашу асимптотически увеличивающуюся дисперсию наблюдений, и в результате выходной сигнал Калмана соответствует очень гладко Но если вы считаете, что существует больше неопределенностей в измерениях, переходах и т. Д., Я думаю, что вы можете обеспечить более высокую ковариацию, и в результате вы получите выход KF не очень плавный (почти после измерений), но асимптотическое увеличение будет отражено в выходная ковариация KF тоже, как показано ниже.
from pykalman import KalmanFilter
import numpy as np
measurements = np.asarray([2, 1, 3, 6, 3, 2, 7, 3, 4, 4, 5, 1, 10, 3, 1, 5])
kf = KalmanFilter(transition_matrices=[1],
observation_matrices=[1],
initial_state_mean=measurements[0],
initial_state_covariance=1,
observation_covariance=5,
transition_covariance=9) #0.01)
state_means, state_covariances = kf.filter(measurements)
state_std = np.sqrt(state_covariances[:,0])
print state_std
print state_means
print state_covariances
import matplotlib.pyplot as plt
plt.plot(measurements, '-r', label='measurment')
plt.plot(state_means, '-g', label='kalman-filter output')
plt.legend(loc='upper left')
plt.show()
measurement_std = [np.std(measurements[:i]) for i in range(len(measurements))]
plt.plot(measurement_std, '-r', label='measurment std')
plt.plot(state_std, '-g', label='kalman-filter output std')
plt.legend(loc='upper left')
plt.show()