Граница, охватывающая заданный набор точек
У меня возникла небольшая проблема с алгоритмом, который я сейчас использую. Я хотел сделать границу.
Вот пример текущего поведения:
https://i.imgur.com/wrhH4wh.png
Вот MSPaint пример желаемого поведения:
Текущий код выпуклой оболочки в C#: https://hastebin.com/dudejesuja.cs
Итак, вот мои вопросы:
1) это вообще возможно?
Р: Да
2) Это даже называется выпуклой оболочкой? (Я так не думаю)
Р: Нет, это называется граница, ссылка: https://www.mathworks.com/help/matlab/ref/boundary.html
3) Будет ли это менее удобным для исполнения, чем обычный выпуклый корпус?
R: Ну, насколько я исследовал, это должно быть то же самое исполнение
4) Пример этого алгоритма в псевдокоде или что-то подобное?
R: Еще не ответили, или я еще не нашел решение
6 ответов
Вот некоторый код Python, который вычисляет альфа-форму (вогнутую оболочку) и сохраняет только внешнюю границу. Это, вероятно, то, что делает граница Matlab внутри.
from scipy.spatial import Delaunay
import numpy as np
def alpha_shape(points, alpha, only_outer=True):
"""
Compute the alpha shape (concave hull) of a set of points.
:param points: np.array of shape (n,2) points.
:param alpha: alpha value.
:param only_outer: boolean value to specify if we keep only the outer border
or also inner edges.
:return: set of (i,j) pairs representing edges of the alpha-shape. (i,j) are
the indices in the points array.
"""
assert points.shape[0] > 3, "Need at least four points"
def add_edge(edges, i, j):
"""
Add an edge between the i-th and j-th points,
if not in the list already
"""
if (i, j) in edges or (j, i) in edges:
# already added
assert (j, i) in edges, "Can't go twice over same directed edge right?"
if only_outer:
# if both neighboring triangles are in shape, it's not a boundary edge
edges.remove((j, i))
return
edges.add((i, j))
tri = Delaunay(points)
edges = set()
# Loop over triangles:
# ia, ib, ic = indices of corner points of the triangle
for ia, ib, ic in tri.vertices:
pa = points[ia]
pb = points[ib]
pc = points[ic]
# Computing radius of triangle circumcircle
# www.mathalino.com/reviewer/derivation-of-formulas/derivation-of-formula-for-radius-of-circumcircle
a = np.sqrt((pa[0] - pb[0]) ** 2 + (pa[1] - pb[1]) ** 2)
b = np.sqrt((pb[0] - pc[0]) ** 2 + (pb[1] - pc[1]) ** 2)
c = np.sqrt((pc[0] - pa[0]) ** 2 + (pc[1] - pa[1]) ** 2)
s = (a + b + c) / 2.0
area = np.sqrt(s * (s - a) * (s - b) * (s - c))
circum_r = a * b * c / (4.0 * area)
if circum_r < alpha:
add_edge(edges, ia, ib)
add_edge(edges, ib, ic)
add_edge(edges, ic, ia)
return edges
Если вы запустите его со следующим тестовым кодом, вы получите этот рисунок, который выглядит так, как вам нужно: 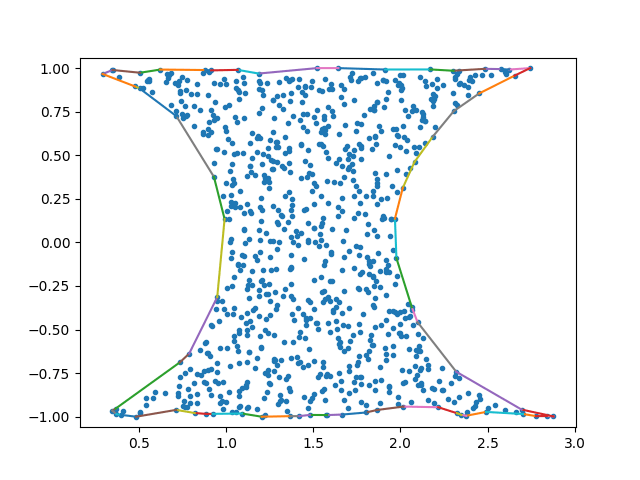
from matplotlib.pyplot import *
# Constructing the input point data
np.random.seed(0)
x = 3.0 * np.random.rand(2000)
y = 2.0 * np.random.rand(2000) - 1.0
inside = ((x ** 2 + y ** 2 > 1.0) & ((x - 3) ** 2 + y ** 2 > 1.0)
points = np.vstack([x[inside], y[inside]]).T
# Computing the alpha shape
edges = alpha_shape(points, alpha=0.25, only_outer=True)
# Plotting the output
figure()
axis('equal')
plot(points[:, 0], points[:, 1], '.')
for i, j in edges:
plot(points[[i, j], 0], points[[i, j], 1])
show()
РЕДАКТИРОВАТЬ: После запроса в комментарии, вот некоторый код, который "сшивает" выходной край, установленный в последовательности последовательных краев.
def find_edges_with(i, edge_set):
i_first = [j for (x,j) in edge_set if x==i]
i_second = [j for (j,x) in edge_set if x==i]
return i_first,i_second
def stitch_boundaries(edges):
edge_set = edges.copy()
boundary_lst = []
while len(edge_set) > 0:
boundary = []
edge0 = edge_set.pop()
boundary.append(edge0)
last_edge = edge0
while len(edge_set) > 0:
i,j = last_edge
j_first, j_second = find_edges_with(j, edge_set)
if j_first:
edge_set.remove((j, j_first[0]))
edge_with_j = (j, j_first[0])
boundary.append(edge_with_j)
last_edge = edge_with_j
elif j_second:
edge_set.remove((j_second[0], j))
edge_with_j = (j, j_second[0]) # flip edge rep
boundary.append(edge_with_j)
last_edge = edge_with_j
if edge0[0] == last_edge[1]:
break
boundary_lst.append(boundary)
return boundary_lst
Затем вы можете просмотреть список граничных списков и добавить точки, соответствующие первому индексу, в каждом ребре, чтобы получить граничный многоугольник.
Я бы использовал другой подход для решения этой проблемы. Поскольку мы работаем с двумерным набором точек, вычислить ограничивающий прямоугольник области точек несложно. Затем я разделил бы этот прямоугольник на "ячейки" горизонтальными и вертикальными линиями, и для каждой ячейки просто посчитал количество пикселей, находящихся в ее границах. Поскольку каждая ячейка может иметь только 4 соседние ячейки (смежные по сторонам ячейки), то граничными ячейками будут те, которые имеют по меньшей мере одну пустую соседнюю ячейку или имеют сторону ячейки, расположенную на границе ограничивающего прямоугольника. Тогда граница будет построена вдоль граничных сторон ячейки. Граница будет выглядеть как "лестница", но выбор меньшего размера ячейки улучшит результат. На самом деле, размер ячейки должен быть определен экспериментально; он не может быть слишком маленьким, иначе внутри области могут появиться пустые ячейки. Среднее расстояние между точками может быть использовано в качестве нижней границы размера ячейки.
Подумайте об использовании Альфа-формы, иногда называемой вогнутым корпусом. https://en.wikipedia.org/wiki/Alpha_shape
Он может быть построен из триангуляции Делоне за время O(N log N).
Как указывало большинство предыдущих экспертов, это может быть не выпуклая оболочка, а вогнутая оболочка, или, другими словами, альфа-форма. Iddo предоставляет чистый код Python для получения этой формы. Однако вы также можете напрямую использовать некоторые существующие пакеты, чтобы реализовать это, возможно, с более высокой скоростью и меньшим объемом вычислительной памяти, если вы работаете с большим количеством облаков точек.
[1] Alpha Shape Toolbox: набор инструментов для создания n-мерных альфа-форм.
[2] Plotly: он может генерировать объект Mesh3d, который в зависимости от значения ключа может быть выпуклой оболочкой этого набора, его триангуляцией Делоне или альфа-набором.
https://plotly.com/python/v3/альфа-формы/https://plotly.com/python/v3/альфа-формы/
Одна из идей заключается в создании треугольников, сетки с использованием облака точек, возможно, с помощью триангуляции Делануэ.
и заполнение этих треугольников цветом, а затем набор уровня запуска или активная сегментация контура, которая найдет внешнюю границу формы, цвет которой теперь отличается от внешнего цвета «фона».
https://xphilipp.developpez.com/contribuez/SnakeAnimation.gif
Анимация выше не прошла весь путь, но многие подобные алгоритмы можно настроить для этого.
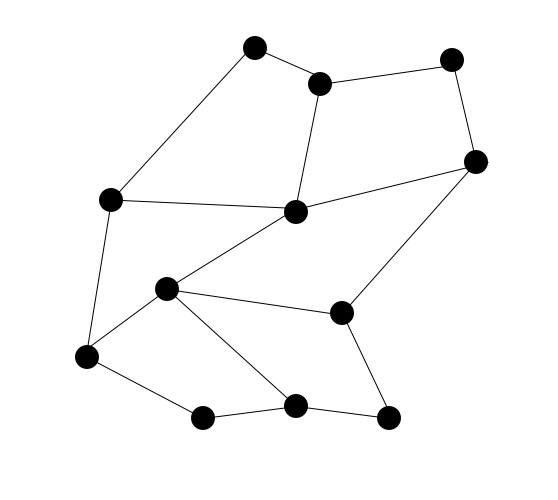
Примечание. Алгоритм триангуляции должен быть настроен таким образом, чтобы он не просто создавал выпуклую оболочку — например, удалял треугольники со слишком большими углами и сторонами из результата делануэя. Предварительный код может выглядеть так
from scipy.spatial import Delaunay
points = np.array([[13.43, 12.89], [14.44, 13.86], [13.67, 15.87], [13.39, 14.95],\
[12.66, 13.86], [10.93, 14.24], [11.69, 15.16], [13.06, 16.24], [11.29, 16.35],\
[10.28, 17.33], [10.12, 15.49], [9.03, 13.76], [10.12, 14.08], [9.07, 15.87], \
[9.6, 16.68], [7.18, 16.19], [7.62, 14.95], [8.39, 16.79], [8.59, 14.51], \
[8.1, 13.43], [6.57, 11.59], [7.66, 11.97], [6.94, 13.86], [6.53, 14.84], \
[5.48, 12.84], [6.57, 12.56], [5.6, 11.27], [6.29, 10.08], [7.46, 10.45], \
[7.78, 7.21], [7.34, 8.72], [6.53, 8.29], [5.85, 8.83], [5.56, 10.24], [5.32, 7.8], \
[5.08, 9.86], [6.01, 5.75], [6.41, 7.48], [8.19, 5.69], [8.23, 4.72], [6.85, 6.34], \
[7.02, 4.07], [9.4, 3.2], [9.31, 4.99], [7.86, 3.15], [10.73, 2.82], [10.32, 4.88], \
[9.72, 1.58], [11.85, 5.15], [12.46, 3.47], [12.18, 1.58], [11.49, 3.69], \
[13.1, 4.99], [13.63, 2.61]])
tri = Delaunay(points,furthest_site=False)
res = []
for t in tri.simplices:
A,B,C = points[t[0]],points[t[1]],points[t[2]]
e1 = B-A; e2 = C-A
num = np.dot(e1, e2)
n1 = np.linalg.norm(e1); n2 = np.linalg.norm(e2)
denom = n1 * n2
d1 = np.rad2deg(np.arccos(num/denom))
e1 = C-B; e2 = A-B
num = np.dot(e1, e2)
denom = np.linalg.norm(e1) * np.linalg.norm(e2)
d2 = np.rad2deg(np.arccos(num/denom))
d3 = 180-d1-d2
res.append([n1,n2,d1,d2,d3])
res = np.array(res)
m = res[:,[0,1]].mean()*res[:,[0,1]].std()
mask = np.any(res[:,[2,3,4]] > 110) & (res[:,0] < m) & (res[:,1] < m )
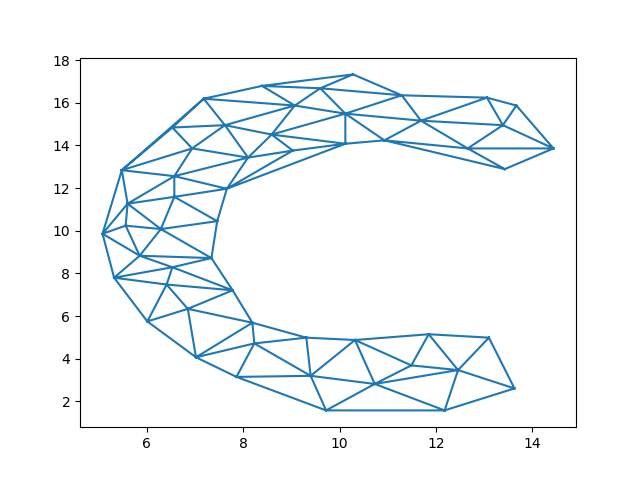
plt.triplot(points[:,0], points[:,1], tri.simplices[mask])
Затем заполните цветом и сегментом.
Вот код JavaScript, который создает вогнутый корпус: https://github.com/AndriiHeonia/hull Вероятно, вы можете перенести его на C#.