Получение более точных результатов из Python SciPy curve_fit

Долгое время скрывался, впервые постер. Заранее благодарны за Вашу помощь.

У меня есть следующий фрагмент кода Python (v2.7.14), который использует curve_fit из SciPy (v1.0.1), чтобы найти параметры для функции экспоненциального затухания. Большую часть времени я получаю разумные результаты. Тем не менее, иногда я получаю некоторые результаты, которые полностью выходят за рамки моего ожидаемого диапазона, даже если найденные параметры будут хорошо выглядеть при построении графика на исходном графике.

Во-первых, мое понимание формулы экспоненциального затухания исходит из https://en.wikipedia.org/wiki/Exponential_decay которую я перевел на Python как:

y = a * numpy.exp(-b * x) + c

Согласно которому:

  • а является начальным значением данных
  • b - скорость затухания, которая является обратной величиной, когда сигнал достигает 1/e от начального значения.
  • с является смещением, так как я имею дело с неотрицательными значениями в моих данных, которые никогда не достигают нуля
  • х текущее время

Скрипт учитывает, что неотрицательные данные подбираются, и корректно смещает первоначальное предположение. Но даже не угадывая, не смещая, используя max/min (вместо первых / последних значений) и другие случайные вещи, которые я пробовал, я не могу заставить команду кривой иметь подходящие значения для проблемных наборов данных.

Моя гипотеза состоит в том, что проблемные наборы данных не имеют достаточной кривой, которую можно уместить, не выходя далеко за пределы области данных. Я посмотрел на аргумент bounds для curve_fit и подумал, что это может быть разумным вариантом. Я не уверен относительно того, что даст хорошие нижние и верхние границы для расчета, или это действительно тот вариант, который я ищу.

Вот код Закомментированный код - это то, что я пробовал.

#!/usr/local/bin/python

import numpy as numpy
from scipy.optimize import curve_fit
import matplotlib.pyplot as pyplot

def exponential_decay(x, a, b, c):
    return a * numpy.exp(-b * x) + c

def fit_exponential(decay_data, time_data, decay_time):
    # The start of the curve is offset by the last point, so subtract
    guess_a = decay_data[0] - decay_data[-1]
    #guess_a = max(decay_data) - min(decay_data)

    # The time that it takes for the signal to reach 1/e becomes guess_b
    guess_b = 1/decay_time

    # Since this is non-negative data, above 0, we use the last data point as the baseline (c)
    guess_c = decay_data[-1]
    #guess_c = min(decay_data)

    guess=[guess_a, guess_b, guess_c]
    print "guess: {0}".format(guess)

    #popt, pcov = curve_fit(exponential_decay, time_data, decay_data, maxfev=20000)
    popt, pcov = curve_fit(exponential_decay, time_data, decay_data, p0=guess, maxfev=20000)

    #bound_lower = [0.05, 0.05, 0.05]
    #bound_upper = [decay_data[0]*2, guess_b * 10, decay_data[-1]]
    #print "bound_lower: {0}".format(bound_lower)
    #print "bound_upper: {0}".format(bound_upper)
    #popt, pcov = curve_fit(exponential_decay, time_data, decay_data, p0=guess, bounds=[bound_lower, bound_upper], maxfev=20000)

    a, b, c = popt

    print "a: {0}".format(a)
    print "b: {0}".format(b)
    print "c: {0}".format(c)

    plot_fit = exponential_decay(time_data, a, b, c)

    pyplot.plot(time_data, decay_data, 'g', label='Data')
    pyplot.plot(time_data, plot_fit, 'r', label='Fit')
    pyplot.legend()
    pyplot.show()

print "Gives reasonable results"
time_data = numpy.array([0.0,0.040000000000000036,0.08100000000000018,0.12200000000000011,0.16200000000000014,0.20300000000000007,0.2430000000000001,0.28400000000000003,0.32400000000000007,0.365,0.405,0.44599999999999995,0.486,0.5269999999999999,0.567,0.6079999999999999,0.6490000000000002,0.6889999999999998,0.7300000000000002,0.7700000000000002,0.8110000000000002,0.8510000000000002,0.8920000000000001,0.9320000000000002,0.9730000000000001])
decay_data = numpy.array([1.342146870531986,1.405586070225509,1.3439802492549762,1.3567811728250267,1.2666276377825874,1.1686375326985337,1.216119360088685,1.2022841507836042,1.1926979408026064,1.1544395213303447,1.1904416926531907,1.1054720201415882,1.112100683833435,1.0811434035632939,1.1221671794680403,1.0673295063196415,1.0036146509494743,0.9984005680821595,1.0134498134883763,0.9996920772051201,0.929782730581616,0.9646581154122312,0.9290690593684447,0.8907360533169936,0.9121560047238627])
fit_exponential(decay_data, time_data, 0.567)

print

print "Gives results that are way outside my expectations"
time_data = numpy.array([0.0,0.040000000000000036,0.08099999999999996,0.121,0.16199999999999992,0.20199999999999996,0.24300000000000033,0.28300000000000036,0.32399999999999984,0.3650000000000002,0.40500000000000025,0.44599999999999973,0.48599999999999977,0.5270000000000001,0.5670000000000002,0.6079999999999997,0.6479999999999997,0.6890000000000001,0.7290000000000001,0.7700000000000005,0.8100000000000005,0.851,0.8920000000000003,0.9320000000000004,0.9729999999999999,1.013,1.0540000000000003])
decay_data = numpy.array([1.4401611921948776,1.3720688158534153,1.3793465463227048,1.2939909686762128,1.3376345321949346,1.3352710161631154,1.3413634841956348,1.248705138603995,1.2914294791901497,1.2581763134585313,1.246975264018646,1.2006447776495062,1.188232179689515,1.1032789127515186,1.163294324147017,1.1686263160765304,1.1434009568472243,1.0511578409946472,1.0814520440570896,1.1035953824496334,1.0626893599266163,1.0645580326776076,0.994855722989818,0.9959891485338087,0.9394584009825916,0.949504060086646,0.9278639431146273])
fit_exponential(decay_data, time_data, 0.6890000000000001)

А вот и вывод текста:

Gives reasonable results
guess: [0.4299908658081232, 1.7636684303350971, 0.9121560047238627]
a: 1.10498934435
b: 0.583046565885
c: 0.274503681044

Gives results that are way outside my expectations
guess: [0.5122972490802503, 1.4513788098693758, 0.9278639431146273]
a: 742.824622191
b: 0.000606308344957
c: -741.41398516

В частности, во втором наборе результатов значение для a очень высокое, причем значение для c одинаково мало на отрицательной шкале, а b - очень маленькое десятичное число.

Вот график первого набора данных, который дает разумные результаты.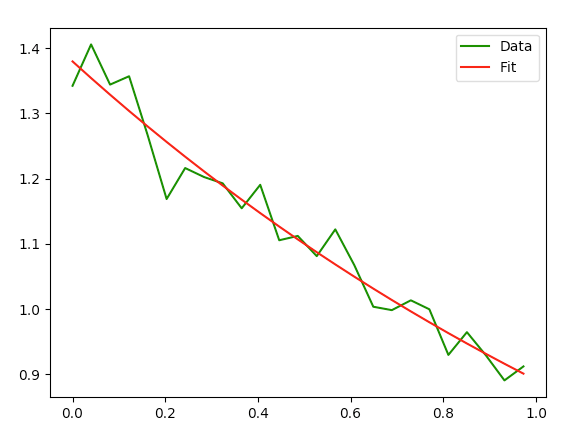Вот график первого набора данных, который дает разумные результаты

Вот график второго набора данных, который не дает хороших результатов.Вот график второго набора данных, который не дает хороших результатов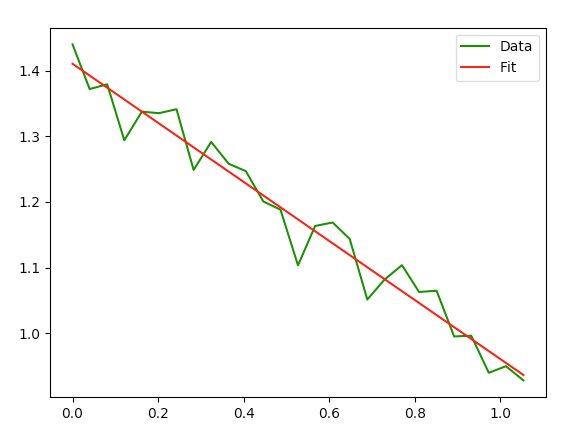

Обратите внимание, что сам график строится правильно, хотя на самом деле линия не имеет хорошей кривой к нему.

Мои вопросы:

  • Верна ли моя реализация алгоритма экспоненциального затухания с кривой_fit?
  • Достаточно ли хороши мои начальные параметры догадки?
  • Является ли параметр границ правильным решением для этой проблемы? Если это так, каков хороший способ определения нижних и верхних границ?
  • Я что-то здесь пропустил?

Еще раз спасибо!

Источник

1 ответ

Когда вы говорите, что второе совпадение дает результаты, которые "выходят за пределы" ваших ожиданий, и что хотя второй график "правильно отображает", линия на самом деле "не соответствует хорошей кривой", вы на правильном пути к пониманию того, что продолжается. Я думаю, что вам просто не хватает части головоломки.

Второй график довольно хорошо соответствует кривой, которая выглядит линейно. Это, вероятно, означает, что у вас на самом деле недостаточно изменений в ваших данных (ну, возможно, ниже уровня шума), чтобы обнаружить, что это экспоненциальный спад.

Могу поспорить, что если вы распечатаете не только наиболее подходящие значения, но также неопределенности и корреляции для переменных, вы увидите, что неопределенности огромны, а некоторые корреляции очень близки к 1. Это может означать, что учтите неопределенности (а измерения всегда имеют неопределенности), результаты могут фактически соответствовать вашим ожиданиям. Это также может указывать на то, что имеющиеся у вас данные не очень хорошо поддерживают экспоненциальный спад.

Вы можете также попробовать другие модели для этих данных (на ум приходит "линейная";)) и сравнить статистические данные о соответствии соответствия, такие как критерий хи-квадрат и информационный критерий Акаике.

scipy.curve_fit возвращает ковариационную матрицу - pcov что вы не использовали в своем примере. К несчастью, scipy.curve_fit не преобразует эти значения в неопределенности и значения корреляции и вообще не пытается вернуть какую-либо статистику соответствия.

Чтобы полностью объяснить любое соответствие данным, вам нужны не только наиболее подходящие значения, но и оценка неопределенностей для переменных параметров. И вам нужна статистика соответствия, чтобы определить, подходит ли соответствие, или, по крайней мере, одно соответствие лучше другого.

Источник
Другие вопросы по тегам