Интерпретация матрицы результатов ковариации

Question

Я пытаюсь понять смысл чтения ковариационной матрицы. Я знаю, что если полученные знаки оба>0, то это означает, что массивы движутся в одном направлении.

x = np.array([[10,39,19,23,28],
              [43,13,32,21,20],
              [15,16,22,85,15]])

print(np.cov(x))

Как интерпретировать этот результат?

[[ 115.7  -120.55  -18.6 ]
 [-120.55  138.7   -76.35]
 [ -18.6   -76.35  933.3 ]]

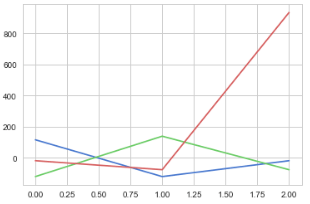
Редактировать: в дополнение к ответу Luca Cappelletti я добавил простой линейный график, чтобы помочь визуализировать распространение (дисперсию) и движение (ковариацию) данных.

Answer 1

Ковариационная матрица

Ковариационная матрица представляет собой симметричную матрицу nxn, где n - это число столбцов матрицы, с которой вы начинаете, и показывает, как переменные вектора коваризуются, то есть, как они имеют тенденцию двигаться относительно друг друга.

Компоненты

На главной диагонали вы найдете дисперсию вектора, а по всем остальным координатам вы найдете ковариацию, поскольку var(X) = cov(X, X).

Положительные и отрицательные коэффициенты

В главной диагонали никакие значения не могут быть отрицательными, поскольку они представляют дисперсию вектора. В любой другой позиции ковариация может быть получена как произведение двух стандартных отклонений (которые всегда неотрицательны) (s (X) и s (Y)) и коэффициента корреляции Пирсона p, который вместо этого изменяется между [-1, 1]: это коэффициент, который делает значения положительными или отрицательными.

cov (X, Y) = p (X, Y) s (X) s (Y)

Есть три варианта:

1. p (X, Y) == 0: нет корреляции между векторами.
2. p (X, Y)> 0: положительная корреляция, означающая, что при увеличении вектора X величина Y увеличивается.
3. p (X, Y) <0: отрицательная корреляция, означающая, что когда вектор X растет, величина Y уменьшается.

Влияние стандартных отклонений на коэффициенты в матрицах является "просто" величиной, то есть они подчеркивают большую корреляцию, когда стандартное отклонение точек данных выше.

Визуализация

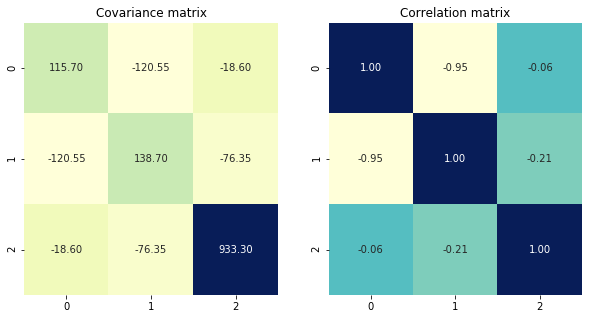
Для лучшей визуализации содержимого матрицы я использую heatmap функция от seaborn пакет Python. Также я добавил корреляционную матрицу для лучшего сравнения результатов.

import numpy as np
from matplotlib import pyplot as plt
import seaborn as sns

x = np.array([[10,39,19,23,28],
            [43,13,32,21,20],
            [15,16,22,85,15]])

plt.rcParams['figure.figsize'] = [10, 5]
plt.axis('scaled')
plt.subplot(1,2,1)
sns.heatmap(np.cov(x), 
        annot=True,
        cbar = False,
        fmt="0.2f",
        cmap="YlGnBu",
        xticklabels=range(len(x)),
        yticklabels=range(len(x)))
plt.title("Covariance matrix")
plt.subplot(1,2,2)
sns.heatmap(np.corrcoef(x), 
        annot=True,
        cbar = False,
        fmt="0.2f",
        cmap="YlGnBu",
        xticklabels=range(len(x)),
        yticklabels=range(len(x)))
plt.title("Correlation matrix")

Выход:

интерпретация

Третий вектор по сравнению с другими имеет исключительно высокую дисперсию. Все векторы имеют отрицательные корреляции, в частности, векторы 1 и 2, которые сильно коррелированы. Векторы 1 и 3 наименее коррелированы.