Определить угловые координаты невыпуклого многоугольника по часовой стрелке MATLAB

Question

У меня есть несколько изображений, которые включают как выпуклые, так и невыпуклые многоугольники. Каждое изображение содержит ровно один многоугольник. Мне нужно определить координаты угла и отсортировать их по часовой стрелке или против часовой стрелки. Для выпуклых многоугольников я использую функцию определения углов Харриса для определения углов и выпуклых для сортировки точек. Но я понятия не имею, как сортировать невыпуклый многоугольник. Поскольку мои входные данные являются изображениями, я думаю, что некоторые методы обработки изображений могут помочь разобраться с ними, двигаясь вдоль края многоугольника. Есть ли способ с наименьшей сложностью?

Пример изображения:

Я назвал углы случайно.

Ожидаемый результат:

Я ожидаю угловые координаты в этом порядке 1 3 5 9 4 2 8 7 6 10 или же 1 10 6 7 8 2 4 9 5 3, Вы можете начать в любой момент, не обязательно 1

Изменить 1:

После решения rayryeng, которое работает для всех выпуклых многоугольников, а также для некоторых невыпуклых многоугольников, существуют некоторые невыпуклые многоугольники, которые не соответствуют его алгоритму.

Вот пример

Answer 1

Другой подход заключается в использовании bwdistgeodesic чтобы найти порядок углов по их расстоянию вдоль вашего края. Это должно работать для любого многоугольника, где вы можете обнаружить непрерывный край.

Мы начнем с загрузки изображения из Stack Overflow и преобразования его в черно-белое изображение, чтобы упростить поиск края.

A = imread('https://stackru.com/images/fcac08f749032ae69b5a26edd1d4f448ca1d708c.jpg');
A_bw = im2bw(A,100/255);  %binary image
A_bw1 = imcomplement(A_bw);   %inverted binary image

bwmorph Функция предоставляет множество опций для манипулирования черно-белыми изображениями. Мы собираемся использовать remove возможность найти ребро нашего полигона, но вы также можете использовать другой детектор ребер, если хотите.

%Find the edges
A_edges = bwmorph(A_bw, 'remove');
[edge_x, edge_y] = find(A_edges');

Давайте визуализируем края, которые мы обнаружили

figure; imshow(A_edges);

Хорошо, у нас есть хорошее четкое непрерывное ребро. Теперь давайте найдем углы. я использую corner, но вы могли бы заменить свой любимый угловой детектор

A_corners = corner(A_bw1, 'QualityLevel',.3);

Давайте представим наш начальный угловой порядок

figure; imshow(A_bw1);
hold on
plot(A_corners(:,1), A_corners(:,2), 'r.', 'MarkerSize', 18)
text(A_corners(:,1), A_corners(:,2), strsplit(num2str(1:length(A_corners))), 'Color', 'g', 'FontSize', 24);
hold off

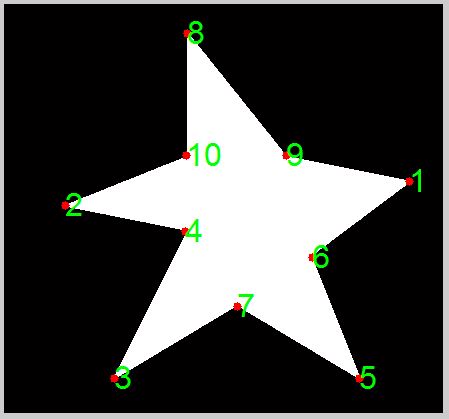
Еще одна вещь, которую вы можете не заметить, это то, что они не по краям. Я начну с нахождения ближайшей точки вдоль края к каждой угловой точке, а затем визуализирую углы красным цветом, а точки ближайшего края - зеленым.

[~, ind] = min(pdist2(A_corners, [edge_x, edge_y]), [], 2);
A_edge_corners = [edge_x(ind), edge_y(ind)];

figure; imshow(A_edges);
hold on;
plot(A_corners(:,1), A_corners(:,2), 'r.', 'MarkerSize', 18)
plot(A_edge_corners(:,1), A_edge_corners(:,2),'g.', 'MarkerSize', 18)
hold off;

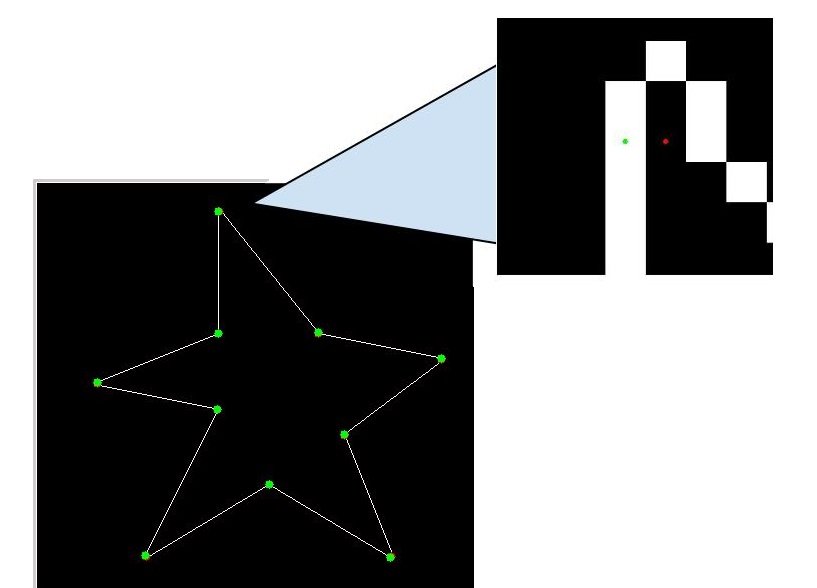
Чтобы вычислить расстояние вокруг края для каждого угла, мы будем использовать приближение угловой точки, A_edge_corners (зеленая точка) на краю, а не сама угловая точка A_corners (красная точка).

Теперь у нас есть все части, которые мы должны использовать bwdistgeodesic, Эта функция находит расстояние до начальной точки для каждого ненулевого пикселя в черно-белом изображении. Нас интересует расстояние от начального угла до каждой точки на краю. Давайте попробуем это.

% Calculate distance from seed corner
first_corner = A_edge_corners(1,:);
D = bwdistgeodesic(A_edges, first_corner(1), first_corner(2));
figure; imagesc(D);

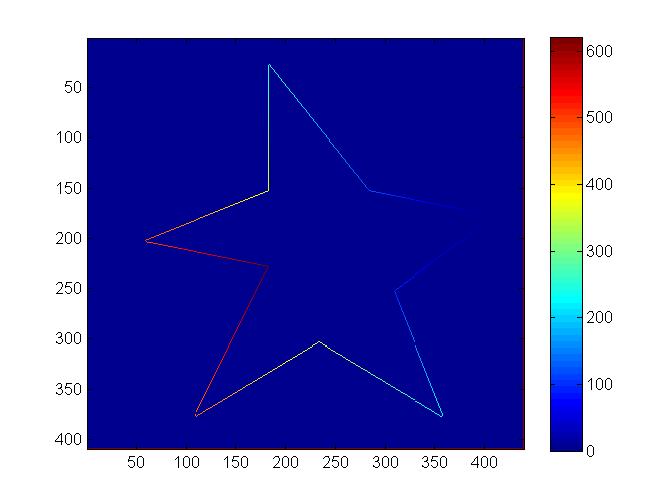
Мы начинаем с самого правого угла, и значение пикселей, удаляющихся от угла, увеличивается. Но это не совсем то, что мы хотим. Если мы упорядочим углы, используя эти значения, мы получим упорядочение по расстоянию от начальной точки.

[~, corner_order] = sort(D(sub2ind(size(D), A_edge_corners(:,2), A_edge_corners(:,1))));
A_corners_reorder1 = A_corners(corner_order, :);

figure; imshow(A_bw1);
hold on
plot(A_corners_reorder1(:,1), A_corners_reorder1(:,2),'r.', 'MarkerSize', 18)
text(A_corners_reorder1(:,1), A_corners_reorder1(:,2), strsplit(num2str(1:length(A_corners))), 'Color', 'g', 'FontSize', 24);
hold off

Чтобы решить эту проблему, нам просто нужно сломать ребро, чтобы упорядочение проходило только в одном направлении от начальной точки. Если вы заинтересованы в упорядочении по часовой стрелке или против часовой стрелки, вам нужно будет разбить ребро в соответствии с набором правил в зависимости от ориентации ребра. Если направление не имеет значения, вы можете просто найти соседний пиксель к начальному углу и разорвать его там.

%Break the edge into one path by removing a pixel adjacent to first corner
%If the corner is near the edge of the image, you would need to check for
%edge conditions
window = A_edges(first_corner(2)-1:first_corner(2)+1, first_corner(1)-1:first_corner(1)+1);
window(2,2) = 0; %Exclude the corner itself
[x, y] = find(window, 1);
A_edges(first_corner(2)+x-2, first_corner(1)+y-2) = 0;  

figure; imshow(A_edges);
hold on;
plot(first_corner(1), first_corner(2), 'r.', 'MarkerSize', 18)
hold off;

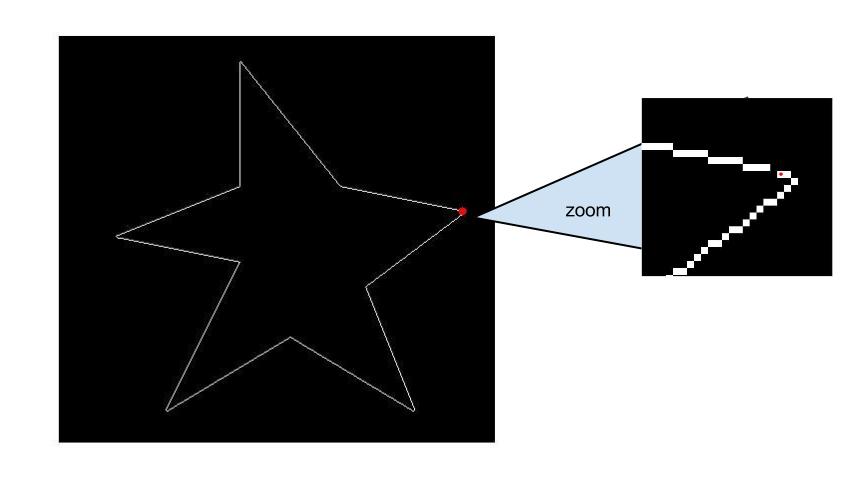
Теперь расстояние от начальной точки по краю может следовать только по одному пути

%Find order the pixels along edge
D = bwdistgeodesic(A_edges, first_corner(1), first_corner(2));
figure; imagesc(D);

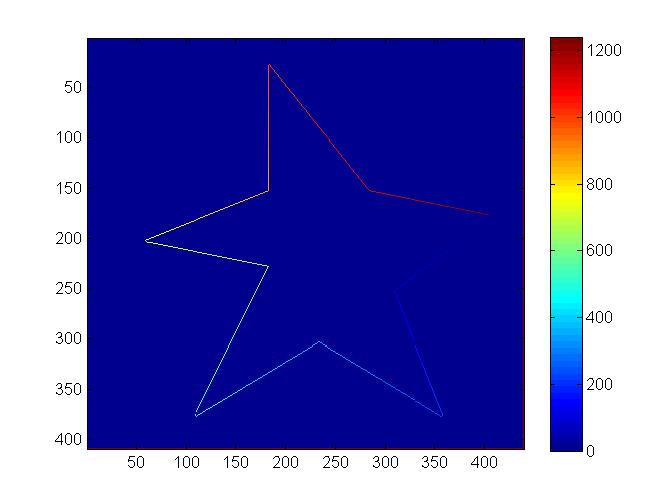
Это дает нам желаемый порядок краев

[~, corner_order] = sort(D(sub2ind(size(D), A_edge_corners(:,2), A_edge_corners(:,1))));
A_corners = A_corners(corner_order, :);

figure; imshow(A_bw1);
hold on
plot(A_corners(:,1), A_corners(:,2),'r.', 'MarkerSize', 18)
text(A_corners(:,1), A_corners(:,2), strsplit(num2str(1:length(A_corners))), 'Color', 'g', 'FontSize', 24);
hold off

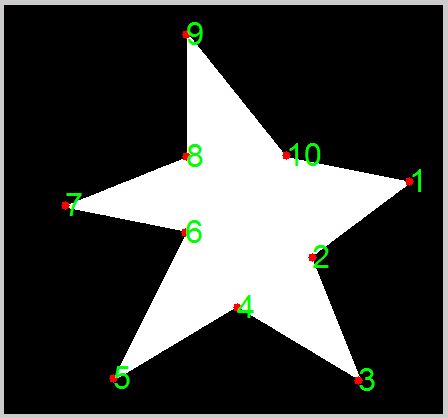
Этот метод также работает с полигонами, которые не сбалансированы относительно центроида, такими как второе демонстрационное изображение.

Для забавы я представляю третье изображение с вершиной на противоположной стороне центроида в качестве более четкого примера несбалансированного многоугольника. Мой метод также правильно анализирует это изображение.

Answer 2

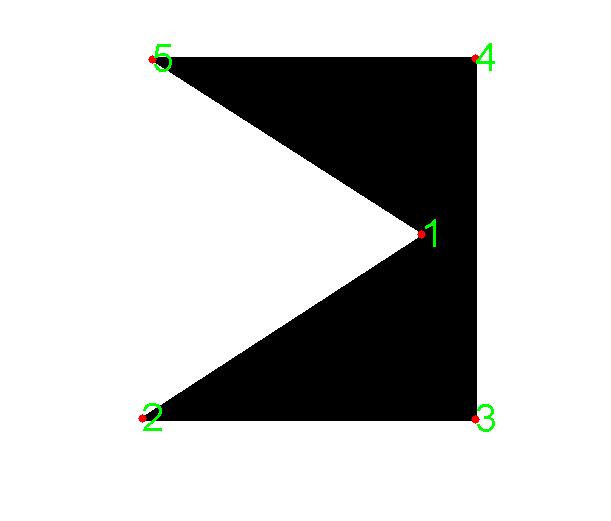
Это распространенная проблема при обработке изображений. Типичный ответ - найти центр тяжести фигуры и найти угол между центром тяжести и каждой угловой точкой. Вы должны убедиться, что углы представлены так, чтобы они находились между [0,360) градусов. Получив это, вы сортируете углы, а затем используете результирующий порядок, чтобы определить порядок точек.

Изображение, которое вы представили, требует предварительной обработки, поэтому я могу начать работу над ним. Я читаю изображение прямо из Stackru, затем инвертирую изображение, чтобы черная звезда стала белой. Мне также нужно удалить цифры, поэтому я использую bwareaopen удалить любые небольшие участки текста. После этого я выполняю определение угла на этом изображении с помощью corner и я установил QualityFactor до 0,3, чтобы я мог обнаружить 10 углов. Очень конкретно:

%// Read image from Stackru
im = rgb2gray(imread('https://stackru.com/images/fcac08f749032ae69b5a26edd1d4f448ca1d708c.jpg'));

%// Threshold the image and area open it
im_thresh = im <= 100;
im_open = bwareaopen(im_thresh, 50);

%// Detect corner points
out = corner(im_open, 'QualityLevel', 0.3);

%// Show the image with the corner points
imshow(im_open);
hold on
plot(out(:,1), out(:,2), 'r.')

im_open содержит наше окончательное обработанное изображение. Вот что я получаю:

---

Теперь давайте найдем центроид. Это может быть просто сделано путем нахождения координат ненулевых местоположений и определения среднего значения каждого измерения:

[rows, cols] = find(im_open);
cenX = mean(cols);
cenY = mean(rows);

cenX а также cenY содержать (x,y) расположение центроида изображения. Просто чтобы убедиться, что мы правильно поняли:

imshow(im_open);
hold on;
plot(cenX, cenY, 'r.', 'MarkerSize', 18);

Мы получаем:

Очень хорошо. Сейчас, out в предыдущем коде содержится (x,y) точки угловых точек. Все, что вам нужно сделать, это определить угол от центроида до каждой угловой точки, а затем отсортировать углы. Вы использовали бы этот порядок сортировки, чтобы переставить угловые точки, чтобы получить упорядоченные точки. Если вы хотите по часовой стрелке, вам нужно будет отсортировать значения в порядке возрастания. Если вы хотите против часовой стрелки, вам нужно будет отсортировать в порядке убывания. Я оставлю это вам на усмотрение того, что вы хотите решить, но я напишу код, который позволит вам сделать то и другое. Поэтому просто сделайте это:

%// Determine angles (in degrees)
angles = atan2d(out(:,2) - cenY, out(:,1) - cenX);

%// Any negative angles, add 360 degrees to convert to positive
angles(angles < 0) = 360 + angles(angles < 0);

%// Sort the angles
[~,ind] = sort(angles); %// clockwise
%[~,ind] = sort(angles, 'descend'); %// counter-clockwise

%// Re-arrange the corner points to respect the order
out_reorder = out(ind,:);

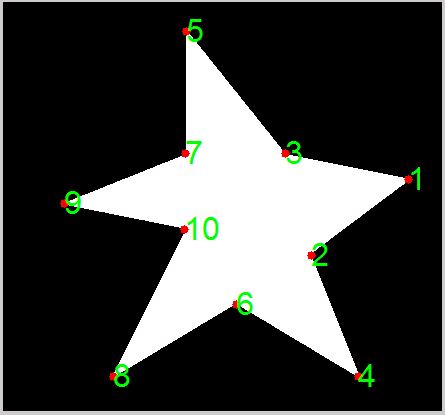
Теперь последний тест состоит в том, чтобы построить эти точки, а также нанести число рядом с каждой точкой, чтобы увидеть, правильно ли мы поняли. Это может быть сделано:

%// Show image
imshow(im_open);
hold on;
%// Show points
plot(out_reorder(:,1), out_reorder(:,2), 'r.', 'MarkerSize', 18);

%// Place a textbox at each point and show a sequence number
for idx = 1 : size(out_reorder,1)
    text(out_reorder(idx,1), out_reorder(idx,2), num2str(idx), 'FontSize', 24, 'Color', 'green');
end

Мы получаем:

Выглядит хорошо для меня! В качестве таких, out_reorder дает вам угловые точки, чтобы они следовали либо по часовой стрелке, либо против часовой стрелки. Каждая строка, с которой вы сталкиваетесь подряд, дает вам следующую точку, которая, естественно, следует за порядком, который вы ищите по часовой стрелке или против часовой стрелки.

Также обратите внимание, где начинается нумерация. Угол 0 определяется горизонтальной линией, которая указывает на восток относительно центроида. Поэтому ближайшая точка к 0, когда мы начинаем в порядке возрастания, - это то место, где вы видите число 1. После 1 вы видите, что оно движется по часовой стрелке, пока у нас не закончатся угловые точки.