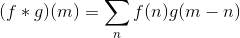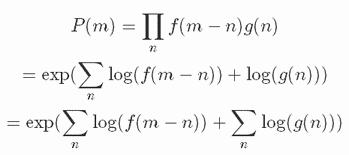Эффективный способ расчета "продукта" дискретной свертки

Question

Я ищу элегантный способ вычисления "продукта" дискретной свертки вместо суммы.

Вот формула дискретной свертки:

В этом случае мы можем использовать: conv(x,y)

Теперь я хотел бы реализовать эти операции

Конечно, я могу использовать цикл, но я ищу хитрость, чтобы линеаризовать эту операцию.

ПРИМЕР:

f = [2 4 3 9 7 1]
g = [3 2 1]

dist = length(g)-1;

for ii = 1:length(f)-dist
    x(ii) = prod(f(ii:ii+dist).*g)
end

х =

144    648   1134    378

Answer 1

Другое решение, частично вдохновленное ответом Dev-iL на относительно тот же вопрос

exp(sum(log(g))+conv(log(f),[1 1 1],'valid'))

или же

exp(sum(log(g))+movsum(log(f),numel(g),'Endpoints', 'discard'))

поскольку exp(sum(log(x))) = prod(x)

Но здесь вместо одного вектора у нас есть два вектора f а также g,

Желаемая формула может быть переформулирована как:

Сроки в октаве:

f= rand(1,1000000);
g= rand(1,100);

disp('----------EXP(LOG)------')
tic
    exp(sum(log(g))+conv(log(f),ones(1,numel(g))));
toc

disp('----------BSXFUN------')
tic
    ind = bsxfun(@plus, 0:numel(f)-numel(g), (1:numel(g)).');
    x = prod(bsxfun(@times, f(ind), g(:)),1);
toc
disp('----------HANKEL------')
tic
    prod(g)*prod(hankel(f(1:numel(g)), f(numel(g):end)));
toc

disp('----------CUMPROD-----')
tic
    pf = cumprod(f);
    x = prod(g)*pf(numel(g):end)./[1 pf(1:(end-numel(g)))];
toc

Результат:

----------EXP(LOG)------%rahnema1
Elapsed time is 0.211445 seconds.
----------BSXFUN--------%Luis Mendo
Elapsed time is 1.94182 seconds.
----------HANKEL--------%gnovice
Elapsed time is 1.46593 seconds.
----------CUMPROD-------%gnovice
Elapsed time is 0.00748992 seconds.

Answer 2

cumprod решение: (очень эффективное)

>> pf = cumprod(f);
>> x = prod(g).*pf(numel(g):end)./[1 pf(1:(end-numel(g)))]

x =

         144         648        1134         378

Это сначала берет совокупный продукт f с помощью cumprod, Разделив каждый элемент на совокупное произведение на 3 элемента перед ним, мы получим произведение каждого numel(g) Широкое раздвижное окно вдоль f, Тогда просто умножьте на произведение элементов g,

ПРИМЕЧАНИЕ: когда f имеет много элементов или экстремальных значений (больших или малых), вы можете столкнуться с проблемами точности или недостаточного / переполнения при выполнении накопительного продукта. Одним из возможных способов смягчения этого было бы применение масштабирования к f перед накопительным продуктом, а затем отмените его:

c = ...set a scaling factor...
pf = cumprod(f./c);
x = prod(c.*g).*pf(numel(g):end)./[1 pf(1:(end-numel(g)))];

Выбор за c может быть что-то вроде mean(abs(f)) или же max(abs(f)) так что масштабируется f дает результаты, которые лучше ограничены (т.е. значения ближе к 1). Это существенно не меняет результаты синхронизации ниже.

---

hankel решение: (не так эффективно, но все же интересно)

>> x = prod(g).*prod(hankel(f(1:numel(g)), f(numel(g):end)))

x =

         144         648        1134         378

Призыв к hankel создает матрицу, в которой каждый столбец содержит содержимое одного из numel(g)раздвижные окна в нем. Убирая произведение вниз по каждому столбцу, затем умножая на произведение элементов g дает ваш ответ. Однако для больших векторов f и / или g это может потребовать много дополнительных вычислений и использовать много памяти.

---

Сроки результатов:

Я проверил 6 решений (цикл в вашем вопросе, 2 решения от Rahnema (conv(log) а также movsum(log)), bsxfun решение от Луиса, и мой cumprod а также hankel решения) с помощью f = rand(1,1000000); а также g = rand(1,100); и в среднем более 40 итераций. Вот что я получил (под управлением Windows 7 x64, 16 ГБ ОЗУ, MATLAB R2016b):

solution    | avg. time (s)
------------+---------------
loop        |       1.10671
conv(log)   |       0.04984
movsum(log) |       0.03736
bsxfun      |       1.20472
cumprod     |       0.01469
hankel      |       1.17704

Answer 3

Вот способ, который избегает петель:

ind = bsxfun(@plus, 0:numel(f)-numel(g), (1:numel(g)).');
x = prod(bsxfun(@times, f(ind), g(:)), 1);

Это работает следующим образом. ind представляет скользящее окно индексов, каждый столбец соответствует смещению. Например, если g имеет размер 3 матрица ind будет

1 2 3 4 ...
2 3 4 5 ...
3 4 5 6 ...

Это используется для индексации в f, Результат умножается (с трансляцией) на g как столбец. Наконец, произведение элементов каждого столбца вычисляется.