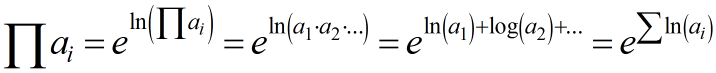Вычислить произведение следующих n элементов в массиве

Я хотел бы рассчитать произведение следующего n смежные элементы матрицы. Число n элементов, которые нужно умножить, должны быть указаны во входных данных функции. Например, для этого ввода я должен вычислить произведение каждых 3 последовательных элементов, начиная с первого.

[p, ind] = max_product([1 2 2 1 3 1],3);

Это дает [1*2*2, 2*2*1, 2*1*3, 1*3*1] = [4,4,6,3],

Есть ли практический способ сделать это? Теперь я делаю это с помощью:

for ii = 1:(length(v)-2)
    p = prod(v(ii:ii+n-1));
end

где v является входным вектором и n количество элементов, которые нужно умножить.

в этом примере n=3 но может принимать любое положительное целочисленное значение.

В зависимости от того n нечетный или четный или length(v) странный или четный, иногда я получаю правильные ответы, но иногда - ошибку.
Например, для аргументов:

v = [1.35912281237829 -0.958120385352704 -0.553335935098461 1.44601450110386 1.43760259196739 0.0266423803393867 0.417039432979809 1.14033971399183 -0.418125096873537 -1.99362640306847 -0.589833539347417 -0.218969651537063 1.49863539349242 0.338844452879616 1.34169199365703 0.181185490389383 0.102817336496793 0.104835620599133 -2.70026800170358 1.46129128974515 0.64413523430416 0.921962619821458 0.568712984110933] 
n = 7

Я получаю ошибку:

Index exceeds matrix dimensions.
Error in max_product (line 6)  
p = prod(v(ii:ii+n-1));

Есть ли правильный общий способ сделать это?

Источник

6 ответов

Решение

Обновить

Вдохновленный хорошо продуманным ответом Dev-iL, приходит это удобное решение, для которого не требуется Matlab R2016a или выше:

out = real( exp(conv(log(a),ones(1,n),'valid')) )

Основная идея состоит в том, чтобы преобразовать умножение в сумму, и можно использовать скользящее среднее, которое, в свою очередь, может быть реализовано conv olution.

Старые ответы

Это один из способов использования gallery получить циркулянтную матрицу и проиндексировать соответствующую часть полученной матрицы перед умножением элементов:

a = [1 2 2 1 3 1]
n = 3

%// circulant matrix
tmp = gallery('circul', a(:))
%// product of relevant parts of matrix
out = prod(tmp(end-n+1:-1:1, end-n+1:end), 2)

out =

     4
     4
     6
     3

Более эффективная память, если на входе нет нулей:

a = [10 9 8 7 6 5 4 3 2 1]
n = 2

%// cumulative product
x = [1 cumprod(a)] 
%// shifted by n and divided by itself
y = circshift( x,[0 -n] )./x 
%// remove last elements 
out = y(1:end-n) 

out =

    90    72    56    42    30    20    12     6     2
Источник

Основываясь на решении в Fast numpy Rolling_Product, я хотел бы предложить его версию MATLAB, которая использует movsum функция введена в R2016a.

Математическое обоснование состоит в том, что произведение чисел равно показателю суммы их логарифмов:

введите описание изображения здесь

Возможная реализация вышеприведенного MATLAB может выглядеть так:

function P = movprod(vec,window_sz)
  P = exp(movsum(log(vec),[0 window_sz-1],'Endpoints','discard'));
  if isreal(vec)   % Ensures correct outputs when the input contains negative and/or
    P = real(P);   %   complex entries.
  end
end

Несколько заметок:

  1. Я не тестировал это решение и не знаю, как оно сравнивается с точки зрения производительности с другими предложениями.
  2. Он должен корректно работать с векторами, содержащими ноль и / или отрицательные и / или сложные элементы.
  3. Его можно легко расширить, чтобы принять измерение для работы (для входов массива) и любые другие настройки, предоставляемые movsum,
  4. Предполагается, что 1- й вход double или complex double вектор строки
  5. Выходы могут потребовать округления.
Источник

Я думаю, что проблема может быть основана на вашей индексации. Линия, которая заявляет for ii = 1:(length(v)-2) не обеспечивает правильный диапазон ii,

Попробуй это:

function out = max_product(in,size)
    size = size-1;                 % this is because we add size to i later
    out = zeros(length(in),1)      % assuming that this is a column vector
    for i = 1:length(in)-size
        out(i) = prod(in(i:i+size));
    end

Ваш код работает при пересчете так:

for ii = 1:(length(v)-(n-1))
    p = prod(v(ii:ii+(n-1)));
end

Это должно позаботиться о проблеме индексации.

Источник

Ваш подход правильный. Вы должны просто изменить цикл for на for ii = 1:(length(v)-n+1) и тогда все будет работать нормально.

Если вы не собираетесь иметь дело с большими входами, другой подход использует gallery как объяснено в ответе @thewaywewalk.

Источник

Используя bsxfun, вы создаете матрицу, каждая строка которой содержит 3 последовательных элемента, а затем берете 2-е измерение матрицы. Я думаю, что это наиболее эффективный способ:

max_product = @(v, n) prod(v(bsxfun(@plus, (1 : n), (0 : numel(v)-n)')), 2);
p = max_product([1 2 2 1 3 1],3)

Обновление: обновлены некоторые другие решения, и некоторые, такие как ответ @Dev-iL, превосходят другие, я могу предложить fftconv что в октаве превосходит conv

Источник

Если вы можете обновить до R2017a, вы можете использовать новую функцию movprod для вычисления оконного продукта.

Источник
Другие вопросы по тегам