Как работает поиск в ширину при поиске кратчайшего пути?
Я провел некоторое исследование, и мне кажется, что мне не хватает одной небольшой части этого алгоритма. Я понимаю, как работает поиск в ширину, но я не понимаю, как именно он приведет меня к определенному пути, а не просто говорит мне, куда может идти каждый отдельный узел. Я думаю, что самый простой способ объяснить мою путаницу - это привести пример:
Так, например, допустим, у меня есть такой график:
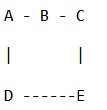
И моя цель - добраться от А до Е (все ребра не взвешены).
Я начинаю с А, потому что это мое происхождение. Я ставлю в очередь А, а затем немедленно снимаю с нее А и исследую его. Это дает B и D, потому что A связан с B и D. Таким образом, я ставлю в очередь и B, и D.
Я снимаю с очереди B и исследую его, и обнаруживаю, что он ведет к A (уже исследованному) и C, поэтому я ставлю в очередь C. Затем я снимаю D с очереди и нахожу, что это приводит к E, моей цели. Затем я снимаю с С и нахожу, что это также приводит к Е, моей цели.
Я логично знаю, что самый быстрый путь - это A->D->E, но я не уверен, как именно помогает поиск в ширину - как я должен записывать пути так, чтобы, когда я закончу, я мог проанализировать результаты и увидеть что кратчайший путь есть A->D->E?
Также обратите внимание, что я на самом деле не использую дерево, поэтому нет "родительских" узлов, только дочерние.
9 ответов
Технически, поиск в ширину (BFS) сам по себе не позволяет найти кратчайший путь, просто потому, что BFS не ищет кратчайший путь: BFS описывает стратегию поиска в графе, но не говорит, что вы должны искать ничего конкретного.
Алгоритм Дейкстры адаптирует BFS, чтобы вы могли найти кратчайшие пути из одного источника.
Чтобы извлечь кратчайший путь от начала координат до узла, вам нужно сохранить два элемента для каждого узла в графе: его текущее кратчайшее расстояние и предыдущий узел в кратчайшем пути. Изначально все расстояния установлены на бесконечность, а все предшествующие - пустые. В вашем примере вы устанавливаете расстояние A на ноль, а затем переходите к BFS. На каждом шаге вы проверяете, можете ли вы улучшить расстояние потомка, то есть расстояние от начала координат до предшественника плюс длина исследуемого ребра меньше текущего наилучшего расстояния для рассматриваемого узла. Если вы можете улучшить расстояние, установите новый кратчайший путь и запомните предшественника, по которому этот путь был получен. Когда очередь BFS пуста, выберите узел (в вашем примере это E) и пройдите его предшественники обратно к источнику. Это даст вам кратчайший путь.
Если это звучит немного странно, в Википедии есть хороший раздел с псевдокодом на эту тему.
Как указано выше, BFS может использоваться только для поиска кратчайшего пути в графе, если:
Нет петель
Все ребра имеют одинаковый вес или не имеют веса.
Чтобы найти кратчайший путь, все, что вам нужно сделать, это начать с источника, выполнить поиск в ширину и остановиться, когда вы найдете целевой узел. Единственное, что вам нужно сделать - это иметь массив previous [n], в котором будет храниться предыдущий узел для каждого посещенного узла. Предыдущий источник может быть нулевым.
Чтобы напечатать путь, просто зациклите предыдущий массив [] от источника до места назначения и распечатайте узлы. DFS также можно использовать для поиска кратчайшего пути в графе при аналогичных условиях.
Однако, если граф более сложен, содержит взвешенные ребра и петли, то нам нужна более сложная версия BFS, то есть алгоритм Дейкстры.
"Он обладает чрезвычайно полезным свойством, что если все ребра в графе не взвешены (или имеют одинаковый вес), то при первом посещении узла это кратчайший путь к этому узлу из исходного узла"
Я потерял 3 дня
в конечном итоге решил вопрос графа
используется для
найти кратчайшее расстояние
используя BFS
Хочу поделиться опытом.
When the (undirected for me) graph has
fixed distance (1, 6, etc.) for edges
#1
We can use BFS to find shortest path simply by traversing it
then, if required, multiply with fixed distance (1, 6, etc.)
#2
As noted above
with BFS
the very 1st time an adjacent node is reached, it is shortest path
#3
It does not matter what queue you use
deque/queue(c++) or
your own queue implementation (in c language)
A circular queue is unnecessary
#4
Number of elements required for queue is N+1 at most, which I used
(dint check if N works)
here, N is V, number of vertices.
#5
Wikipedia BFS will work, and is sufficient.
https://en.wikipedia.org/wiki/Breadth-first_search#Pseudocode
Я потерял 3 дня, пробуя все вышеперечисленные альтернативы, проверяя и проверяя снова и снова выше
они не проблема.
(Попробуйте потратить время на поиск других проблем, если вы не нашли каких-либо проблем с выше 5).
Больше объяснений из комментария ниже:
A
/ \
B C
/\ /\
D E F G
Предположим, выше ваш график
график идет вниз
Для A смежными являются B & C
Для B смежными являются D & E
Для C смежными являются F & G
скажем, начальный узел A
когда вы достигаете A, к, B & C кратчайшее расстояние до B & C от A составляет 1
когда вы достигаете D или E, через B, кратчайшее расстояние до A & D составляет 2 (A->B->D)
аналогично, A->E равно 2 (A->B->E)
также A->F & A->G равно 2
Итак, теперь вместо 1 расстояния между узлами, если оно равно 6, просто умножьте ответ на 6
пример,
если расстояние между каждым равно 1, то A-> E равно 2 (A->B->E = 1+1)
если расстояние между ними равно 6, то A-> E равно 12 (A->B->E = 6+6)
да, БФС может пойти по любому пути
но мы рассчитываем для всех путей
если вам нужно перейти от A к Z, то мы пройдем все пути от A до промежуточного I, и поскольку будет много путей, мы отбрасываем все пути, кроме I, до I, затем продолжаем с кратчайшим путем до следующего узла J
опять же, если есть несколько путей от I до J, мы берем только самый короткий
пример,
предполагать,
A -> У меня есть расстояние 5
(ШАГ) предположим, что I -> J, у нас есть несколько путей с расстояниями 7 и 8, так как 7 - самое короткое
мы берем A -> J как 5 (A->I самый короткий) + 8 (самый короткий сейчас) = 13
так что A-> J сейчас 13
мы повторяем теперь выше (ШАГ) для J -> K и так далее, пока не дойдем до Z
Прочитайте эту часть 2 или 3 раза и нарисуйте на бумаге, вы, несомненно, получите то, что я говорю, удачи
Посещение этой темы после некоторого периода бездействия, но с учетом того, что я не вижу подробного ответа, вот мои два цента.
Поиск в ширину всегда находит кратчайший путь в невзвешенном графе. График может быть циклическим или ациклическим.
См. Псевдокод ниже. Этот псевдокод предполагает, что вы используете очередь для реализации BFS. Также предполагается, что вы можете пометить вершины как посещенные и что каждая вершина хранит параметр расстояния, который инициализируется как бесконечность.
mark all vertices as unvisited
set the distance value of all vertices to infinity
set the distance value of the start vertex to 0
if the start vertex is the end vertex, return 0
push the start vertex on the queue
while(queue is not empty)
dequeue one vertex (we’ll call it x) off of the queue
if x is not marked as visited:
mark it as visited
for all of the unmarked children of x:
set their distance values to be the distance of x + 1
if the value of x is the value of the end vertex:
return the distance of x
otherwise enqueue it to the queue
if here: there is no path connecting the vertices
Обратите внимание, что этот подход не работает для взвешенных графов - для этого см. Алгоритм Дейкстры.
На основании ответа acheron55 я разместил здесь возможную реализацию.
Вот краткое изложение этого:
Все, что вам нужно сделать, это отслеживать путь, по которому была достигнута цель. Простой способ сделать это, это нажать на Queue весь путь, используемый для достижения узла, а не сам узел.
Преимущество этого состоит в том, что когда цель достигнута, очередь содержит путь, используемый для ее достижения.
Это также применимо к циклическим графам, где узел может иметь более одного родителя.
У меня было такое же непонимание. Мне потребовалось некоторое время, чтобы понять, как BFS находит кратчайший путь между любыми двумя узлами.
К сожалению, большинство ответов бесполезны и запутывают дело, без необходимости прибегая к алгоритму Джикстры. Я расширим ответ Химаншу, который поднял решающий момент, что...
Просто по тому, как BFS проходит граф, любой узел, которого он достигает, является кратчайшим путем к этому узлу от исходного узла. Предположим, нам нужно найти путь DC в следующем простом графе. Следуйте вперед, используя ручку и бумагу.
Мы начинаем с D и исследуем граф с помощью BFS. Вы видите, что мы обязательно доберемся до С через В, а не до А, потому что В будет первым в нашем обходе. Вот почему мы думаем об узлах как о родителях и потомках и почему эта информация сохраняется в виде словаря, когда мы движемся по графу для последующего поиска для построения пути. Предположим, что этот словарь называется «rel_dict», rel для отношения.
Увеличим этот график (для графика добавлены картинка и код). Теперь мы увидим, что для нахождения пути между любыми двумя узлами важно начать с одного из двух узлов. Потому что, если мы выберем третий узел, rel_dict, сформированный таким образом в конце обхода BFS, возможно, не даст кратчайшего пути, а вместо этого либо вообще не даст пути, либо укажет более длинный.
import networkx as nx
import matplotlib.pyplot as plt
d = {
"A": ["B", "C"],
"B": ["A", "D", "E", "C"],
"C": ["A", 'B', "F"],
"D": ["B"],
"E": ["B", "G"],
"F": ["C"],
"G": ["E"]
}
g = nx.Graph(d)
nx.draw_networkx(g)
plt.draw()
plt.show()
Чтобы удалить узел из очереди, мы ставим в очередь его дочерние элементы, если они есть. Одновременно для каждого посещаемого узла мы сопоставляем его родителю в словаре rel_dict. Мы продолжаем делать это, пока очередь не опустеет. Затем, чтобы построить путь между начальным узлом и любым другим узлом, мы берем конечный узел, находим его родителя, затем находим родителя этого родителя и так далее, пока не найдем начальный узел, и мы это сделаем. Сделайте это упражнение ручкой и бумагой: вам нужно будет поддерживать очередь и rel_dict. Затем постройте путь в обратном порядке.
Теперь попробуйте найти путь между любыми двумя узлами, ни один из которых не был начальным, и вы увидите, что это не дает правильного ответа.
Хорошее объяснение того, как BFS вычисляет кратчайшие пути, в сопровождении наиболее эффективного простого алгоритма BFS, о котором я знаю, а также рабочего кода, представлено в следующей рецензируемой статье:
https://queue.acm.org/detail.cfm?id=3424304
В документе объясняется, как BFS вычисляет дерево кратчайших путей, представленное родительскими указателями для каждой вершины, и как восстановить конкретный кратчайший путь между любыми двумя вершинами из родительских указателей. Объяснение BFS принимает три формы: проза, псевдокод и работающая программа на C.
В статье также описывается "Эффективный BFS" (E-BFS), простой вариант классического учебного BFS, который повышает его эффективность. В асимптотическом анализе время работы улучшается с Theta(V+E) до Omega(V). На словах: классический BFS всегда работает по времени, пропорциональному количеству вершин плюс количество ребер, тогда как E-BFS иногда работает по времени, пропорциональному только количеству вершин, которое может быть намного меньше. На практике E-BFS может быть намного быстрее, в зависимости от входного графика. E-BFS иногда не дает преимуществ перед классической BFS, но никогда не намного медленнее.
Примечательно, что, несмотря на свою простоту, E-BFS не получил широкой известности.
Следующее решение работает для всех тестовых случаев.
import java.io.*;
import java.util.*;
import java.text.*;
import java.math.*;
import java.util.regex.*;
public class Solution {
public static void main(String[] args)
{
Scanner sc = new Scanner(System.in);
int testCases = sc.nextInt();
for (int i = 0; i < testCases; i++)
{
int totalNodes = sc.nextInt();
int totalEdges = sc.nextInt();
Map<Integer, List<Integer>> adjacencyList = new HashMap<Integer, List<Integer>>();
for (int j = 0; j < totalEdges; j++)
{
int src = sc.nextInt();
int dest = sc.nextInt();
if (adjacencyList.get(src) == null)
{
List<Integer> neighbours = new ArrayList<Integer>();
neighbours.add(dest);
adjacencyList.put(src, neighbours);
} else
{
List<Integer> neighbours = adjacencyList.get(src);
neighbours.add(dest);
adjacencyList.put(src, neighbours);
}
if (adjacencyList.get(dest) == null)
{
List<Integer> neighbours = new ArrayList<Integer>();
neighbours.add(src);
adjacencyList.put(dest, neighbours);
} else
{
List<Integer> neighbours = adjacencyList.get(dest);
neighbours.add(src);
adjacencyList.put(dest, neighbours);
}
}
int start = sc.nextInt();
Queue<Integer> queue = new LinkedList<>();
queue.add(start);
int[] costs = new int[totalNodes + 1];
Arrays.fill(costs, 0);
costs[start] = 0;
Map<String, Integer> visited = new HashMap<String, Integer>();
while (!queue.isEmpty())
{
int node = queue.remove();
if(visited.get(node +"") != null)
{
continue;
}
visited.put(node + "", 1);
int nodeCost = costs[node];
List<Integer> children = adjacencyList.get(node);
if (children != null)
{
for (Integer child : children)
{
int total = nodeCost + 6;
String key = child + "";
if (visited.get(key) == null)
{
queue.add(child);
if (costs[child] == 0)
{
costs[child] = total;
} else if (costs[child] > total)
{
costs[child] = total;
}
}
}
}
}
for (int k = 1; k <= totalNodes; k++)
{
if (k == start)
{
continue;
}
System.out.print(costs[k] == 0 ? -1 : costs[k]);
System.out.print(" ");
}
System.out.println();
}
}
}