Расширение заговора

Question

У меня есть следующий код для моего теоретического анализа с использованием экспериментальных данных. Я пытаюсь подогнать кривую и экстраполировать значения S_u0, чтобы определить начальные температуры.

# Determination of laminar burning velocities from experimental data using constant volume pressure rise method.
import numpy as np
import openpyxl as xl
import matplotlib.pylab as plt
from lmfit import Model
plt.rc('font',family='Book Antiqua',size=12)

p_i=float(2.0)                 # Initial pressure
c=float(2.0265)                # Constant
V_b=float(1.94e-3)             # Volume of combustion bomb
k_u=float(1.3)                 # Specific heat ratio of unburnt mass
k_b=float(1.27)                # Specific heat ratio of burnt mass

# Extracting experimental data from excel.
wb = xl.load_workbook("G:/Laminar Paper/Data/T0444CH1.xlsx")
ws = wb.active

# Calculation of  initial voltage from experimental values.
num_cells=list(ws['B2':'B1500'])
V_initial=[]
for row in num_cells:
    for cell in row:
        V_initial.append(cell.value)
V_av=np.absolute(sum(V_initial)/len(V_initial))          # Average voltage

# Determining the final voltage from the experimental values.
num_cells=list(ws['B3':'B13252'])
V_final=[]                                                    # Experimental testing voltages
for row in num_cells:
    for cell in row:
        V_final.append(cell.value)
p=(V_final/np.floor(c))+(p_i-(V_av/np.floor(c)))              # Combustion pressure

# The time elapse.
num_cells=list(ws['A3':'A13252'])
time=[]
for row in num_cells:
    for cell in row:
        time.append(cell.value)

# Curve fitting.
Func_1=np.polyfit(time, p, 15)
Func_2=np.poly1d(Func_1)
time_new=np.linspace(time[0], time[-1], 50)                   # New time values
p_new=Func_2(time_new)                                        # New pressure values/filtered pressure
dp_dt=np.gradient(p_new,time_new)                             # Derivative of pressure wrt time

# Linear approximation method.
x_linear=(p_new-p_i)/(max(p_new)-p_i)                         # Burnt mass fraction
R_b=(pow(((V_b*3)/(4*np.pi)), 1.0/3))
S_u1=((1-(1-x_linear)*(p_i/p_new)**1/k_u)**-2/3)
S_u2=S_u1*((p_i/p_new)*1/k_u)
S_u3=S_u2*(1/(max(p_new)-p_i))*dp_dt
S_u=(R_b/3)*S_u3                                              # Linear approximation laminar flame speed

# Two-zone approach.
func_p=(k_b-1)/(k_u-1)+(((k_u-k_b)/(k_u-1))*(p_new/p_i)**((k_u-1)/k_u))
x_2zone=(p_new-p_i*func_p)/(max(p)-p_i*func_p)                                # Burnt mass fraction
S_uz1=((1-(1-x_2zone)*(p_i/p_new)**1/k_u)**-2/3)
S_uz2=S_uz1*((p_i/p_new)*1/k_u)
S_uz3=S_uz2*(1/(max(p_new)-p_i))*dp_dt
S_uz=(R_b/3)*S_uz3                                                            # Two-zone laminar flame speed

# Model function.
def mod_m(n,su0=1,alpha=1):
    return su0*(n)**alpha

# S_u and pressure ratio  array data for fitting and calculating S_u0 and T_0.
n=np.array([1.78759326,1.91173221,2.05673713,2.22911249,2.4360555,2.68433232,2.97885016])
m=np.array([0.20791161,0.20332239,0.20206572,0.20260075,0.20292399,0.20115307,0.19601662])

# Fitting model.
model=Model(mod_m)

# Making a set of parameters (for 'su0' and 'alpha'):
params=model.make_params(s_u0=10)

# Setting  min/max bounds on parameters:
params['alpha'].min=0.0
params['su0'].min=0.0
params['su0'].max=1e2

# Run the fit with Model.fit(Data_Array, Parameters, independent vars).
result=model.fit(m,params,n=n)

# Plotting.
plt.plot(n,result.best_fit,'b*-', label='Fit')
plt.plot(p_new/p_i,S_u,'k--',linewidth='2',label='Linear')
plt.plot(p_new/p_i,S_uz,'r-',label='Two-zone')
plt.xlabel('Pressure ratio $p/p_i$')
plt.ylabel('Laminar flame speed $(S_u)$ [m/s]')
plt.legend(loc='lower right')
plt.savefig('Laminar.png')
plt.show()

# Printing  report with results and fitting statistics.
print(result.fit_report())

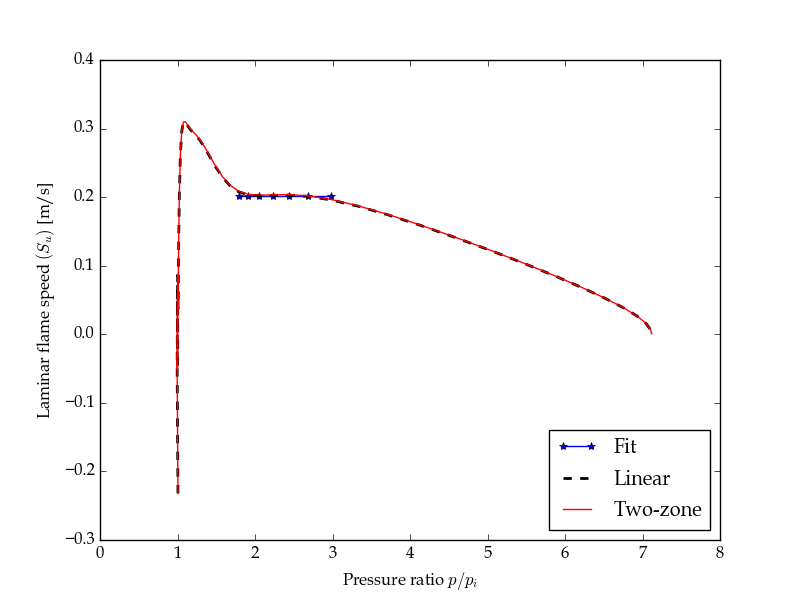
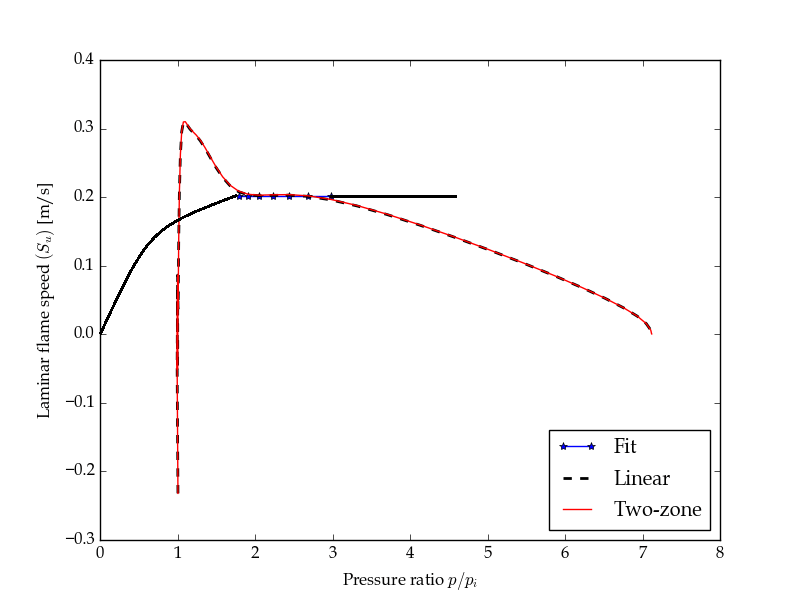
После построения графика я получил рисунок 1, но я хочу получить график, похожий на рисунок 2. Пожалуйста, как мне получить рисунок, похожий на рисунок 2. Заранее спасибо.

Рисунок 1

фигура 2

Answer 1

Если я понимаю вопрос, вы хотите построить прогнозные значения модели вне диапазона, используемого для подгонки.

С вашим ограниченным диапазоном для n а также m массивы (по крайней мере, по сравнению с другими вашими данными)

result = model.fit(m, params, n=n)
plt.plot(n, result.best_fit, 'b*-', label='Fit')

будет наносить только на ограниченный диапазон, который вы использовали для подгонки.

Вы можете оценить модель с помощью набора параметров (вы, вероятно, хотите, чтобы параметры наилучшего соответствия) и любых значений независимой переменной nс result.eval():

new_m = result.eval(result.params, n=new_n)

Кажется, что вы хотите, может быть что-то вроде

new_n = np.linspace(0, 5, 51)[1:]  # to avoid 0, where your model fails
plt.plot(new_n, result.eval(result.params, n=new_n), label='Predicted')