Как получить ошибки параметров из оценки максимального правдоподобия с известной функцией правдоподобия в python?

Question

У меня есть некоторые данные и я хочу соответствовать заданной психометрической функции p. 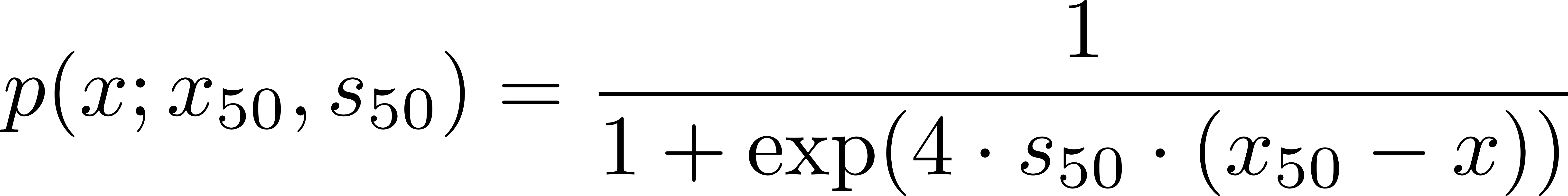Меня также интересуют параметры подгонки и ошибки. С помощью "классического" метода с использованием функции curve_fit из пакета scipy легко получить параметры p и ошибки. Однако я хочу сделать то же самое, используя оценку максимального правдоподобия (MLE). Из вывода и рисунка видно, что оба метода предлагают несколько разные параметры. Реализация MLE не является проблемой, но я не знаю, как получить ошибки, используя этот метод. Есть ли простой способ получить их? Моя функция правдоподобия L: Я не смог адаптировать описанный здесь код http://rlhick.people.wm.edu/posts/estimating-custom-mle.html но это, вероятно, решение. Как я могу это реализовать? Или это есть какой-то другой путь?

Подобная функция используется здесь с использованием моделей статистики scipy: https://stats.stackexchange.com/questions/66199/maximum-likelihood-curve-model-fitting-in-python. Однако ошибки параметров также не рассчитываются.

Функция отрицательного логарифмического правдоподобия верна, поскольку она предлагает правильные параметры, но мне было интересно, зависит ли эта функция от y-данных? Функция отрицательного логарифмического правдоподобия l, очевидно, равна l = -ln(L). Вот мой код:

#!/usr/bin/env python
# -*- coding: utf-8 -*- 

## libary
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
from scipy.optimize import minimize


def p(x,x50,s50):
    """return y value of psychometric function p"""
    return 1./(1+np.exp(4.*s50*(x50-x)))

def initialparams(x,y):
    """return initial fit parameters for function p with given dataset"""
    midpoint = np.mean(x)
    slope = (np.max(y)-np.min(y))/(np.max(x)-np.min(x))
    return [midpoint, slope]

def cfit_error(pcov):
    """return errors of fir from covariance matrix"""
    return np.sqrt(np.diag(pcov))

def neg_loglike(params):
    """analytical negative log likelihood function. This function is dependend on the dataset (x and y) and the two parameters x50 and s50."""
    x50 = params[0]
    s50 = params[1]
    i = len(xdata)
    prod = 1.
    for i in range(i):
        #print prod
        prod *= p(xdata[i],x50,s50)**(ydata[i]*5) * (1-p(xdata[i],x50,s50))**((1.-ydata[i])*5)
    return -np.log(prod)


xdata = [0.,-7.5,-9.,-13.500001,-12.436171,-16.208617,-13.533123,-12.998025,-13.377527,-12.570075,-13.320075,-13.070075,-11.820075,-12.070075,-12.820075,-13.070075,-12.320075,-12.570075,-11.320075,-12.070075]
ydata = [1.,0.6,0.8,0.4,1.,0.,0.4,0.6,0.2,0.8,0.4,0.,0.6,0.8,0.6,0.2,0.6,0.,0.8,0.6]

intparams = initialparams(xdata, ydata)## guess some initial parameters


## normal curve fit using least squares algorithm
popt, pcov = curve_fit(p, xdata, ydata, p0=intparams)
print('scipy.optimize.curve_fit:')
print('x50 = {:f} +- {:f}'.format(popt[0], cfit_error(pcov)[0]))
print('s50 = {:f} +- {:f}\n'.format(popt[1], cfit_error(pcov)[1]))



## fitting using maximum likelihood estimation
results = minimize(neg_loglike, initialparams(xdata,ydata), method='Nelder-Mead')
print('MLE with self defined likelihood-function:')
print('x50 = {:f}'.format(results.x[0]))
print('s50 = {:f}'.format(results.x[1]))
#print results


## ploting the data and results
xfit = np.arange(-20,1,0.1)

fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.plot(xdata, ydata, 'xb', label='measured data')
ax.plot(xfit, p(xfit, *popt), '-r', label='curve fit')
ax.plot(xfit, p(xfit, *results.x), '-g', label='MLE')
plt.legend()
plt.show()

Выход:

scipy.optimize.curve_fit:
x50 = -12.681586 +- 0.252561
s50 = 0.264371 +- 0.117911

MLE with self defined likelihood-function:
x50 = -12.406544
s50 = 0.107389

И подгонки, и измеренные данные можно увидеть здесь: Моя версия Python 2.7 на Debian Stretch. Спасибо за помощь.

Answer 1

Наконец-то был разработан метод, описанный Робом Хиксом ( http://rlhick.people.wm.edu/posts/estimating-custom-mle.html). После установки numdifftools я смог вычислить ошибки оценочных параметров по гессианской матрице.

Установка numdifftools в Linux с правами su:

apt-get install python-pip
pip install numdifftools

Полный пример кода моей программы сверху здесь:

#!/usr/bin/env python
# -*- coding: utf-8 -*- 

## libary
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
from scipy.optimize import minimize
import numdifftools as ndt



def p(x,x50,s50):
    """return y value of psychometric function p"""
    return 1./(1+np.exp(4.*s50*(x50-x)))

def initialparams(x,y):
    """return initial fit parameters for function p with given dataset"""
    midpoint = np.mean(x)
    slope = (np.max(y)-np.min(y))/(np.max(x)-np.min(x))
    return [midpoint, slope]

def cfit_error(pcov):
    """return errors of fir from covariance matrix"""
    return np.sqrt(np.diag(pcov))

def neg_loglike(params):
    """analytical negative log likelihood function. This function is dependend on the dataset (x and y) and the two parameters x50 and s50."""
    x50 = params[0]
    s50 = params[1]
    i = len(xdata)
    prod = 1.
    for i in range(i):
        #print prod
        prod *= p(xdata[i],x50,s50)**(ydata[i]*5) * (1-p(xdata[i],x50,s50))**((1.-ydata[i])*5)
    return -np.log(prod)


xdata = [0.,-7.5,-9.,-13.500001,-12.436171,-16.208617,-13.533123,-12.998025,-13.377527,-12.570075,-13.320075,-13.070075,-11.820075,-12.070075,-12.820075,-13.070075,-12.320075,-12.570075,-11.320075,-12.070075]
ydata = [1.,0.6,0.8,0.4,1.,0.,0.4,0.6,0.2,0.8,0.4,0.,0.6,0.8,0.6,0.2,0.6,0.,0.8,0.6]



intparams = initialparams(xdata, ydata)## guess some initial parameters


## normal curve fit using least squares algorithm
popt, pcov = curve_fit(p, xdata, ydata, p0=intparams)
print('scipy.optimize.curve_fit:')
print('x50 = {:f} +- {:f}'.format(popt[0], cfit_error(pcov)[0]))
print('s50 = {:f} +- {:f}\n'.format(popt[1], cfit_error(pcov)[1]))



## fitting using maximum likelihood estimation
results = minimize(neg_loglike, initialparams(xdata,ydata), method='Nelder-Mead')
## calculating errors from hessian matrix using numdifftools
Hfun = ndt.Hessian(neg_loglike, full_output=True)
hessian_ndt, info = Hfun(results.x)
se = np.sqrt(np.diag(np.linalg.inv(hessian_ndt)))

print('MLE with self defined likelihood-function:')
print('x50 = {:f} +- {:f}'.format(results.x[0], se[0]))
print('s50 = {:f} +- {:f}'.format(results.x[1], se[1]))

Создает следующий вывод:

scipy.optimize.curve_fit:
x50 = -18.702375 +- 1.246728
s50 = 0.063620 +- 0.041207

MLE with self defined likelihood-function:
x50 = -18.572181 +- 0.779847
s50 = 0.078935 +- 0.028783

Однако при вычислении гессианской матрицы с помощью numdifftools возникают некоторые RuntimeErrors. Есть какое-то деление на ноль. Это может быть из-за моей собственной функции neg_loglike. В конце есть некоторые результаты для ошибок. Метод с использованием "Расширения Statsmodels", вероятно, более элегантен, но я не мог понять это.