Более быстрый метод расчета волатильности портфеля

Question

Я пишу функцию Numba для расчета волатильности портфеля:

Некоторые функции, которые я использую для этого, находятся здесь:

import numba as nb
import numpy as np

def portfolio_s2( cv, weights ):
    """ Calculate the variance of a portfolio """
    return weights.dot( cv ).dot( weights )

@nb.jit( nopython=True )
def portfolio_s2c( cv, weights ):

    s0 = 0.0
    for i in range( weights.shape[0]-1 ):
        wi = weights[i]
        s0 += cv[i,i]*wi*wi
        s1 = 0.0
        for j in range( i+1, weights.shape[0] ):
            s1 += wi*weights[j]*cv[i,j]
        s0 += 2.0*s1

    i = weights.shape[0]-1 
    wi = weights[ i ]
    s0 += cv[i,i]*wi**2
    return s0

@nb.jit( nopython=True )
def portfolio_s2b( cv, weights ):

    s0 = 0.0
    for i in range( weights.shape[0] ):
        s0 += weights[i]*weights[i]*cv[i,i]

    s1 = 0.0
    for i in range( weights.shape[0]-1 ):
        s2 = 0.0
        for j in range( i+1, weights.shape[0] ):
            s2 += weights[j]*cv[i,j]
        s1+= weights[i]*s2
    return s0+2.0*s1 

Я проверяю производительность функций с помощью этого кода:

    N = 1000
    num_tests = 10000

    times_2b = []
    times_2c = []
    times_np = []

    matrix_sizes = [ 2,4,8, 10, 20, 40, 80, 160 ]#, 320, 640, 1280, 2560 ]

    for m in matrix_sizes:
        X = np.random.randn( N, m )
        cv = np.cov( X, rowvar=0 )

        w = np.ones( cv.shape[0] ) / cv.shape[0]

        s2 = helpers.portfolio_s2( cv, w )
        s2b = helpers.portfolio_s2b( cv, w )
        s2c = helpers.portfolio_s2c( cv, w )

        np.testing.assert_almost_equal( s2, s2b ) 
        np.testing.assert_almost_equal( s2, s2c )               

        with Timer( 'nb2b' ) as t2b:
            for _ in range(num_tests):
                helpers.portfolio_s2b( cv, w )

        with Timer( 'nb2c' ) as t2c:
            for _ in range(num_tests):
                helpers.portfolio_s2c( cv, w )                

        with Timer( 'np' ) as tnp:
            for _ in range(num_tests):
                helpers.portfolio_s2( cv, w )

        times_2b.append( t2b.timetaken )
        times_2c.append( t2c.timetaken )
        times_np.append( tnp.timetaken )

    plt.figure()
    plt.plot( matrix_sizes, times_2b, label='2b' )
    plt.plot( matrix_sizes, times_2c, label='2c' )
    plt.plot( matrix_sizes, times_np, label='np' )
    plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
    plt.show()

Это класс Timer:

import time
class Timer( object ):

    def __init__(self, name=''):
        self._name = name

    def __enter__(self):
        self.start = time.time()
        return self        

    def __exit__(self,a,b,c):
        self.end = time.time()
        self.timetaken = self.end-self.start
        print( '{0} Took {1} seconds'.format( self._name, self.timetaken ))

Результаты представлены здесь:

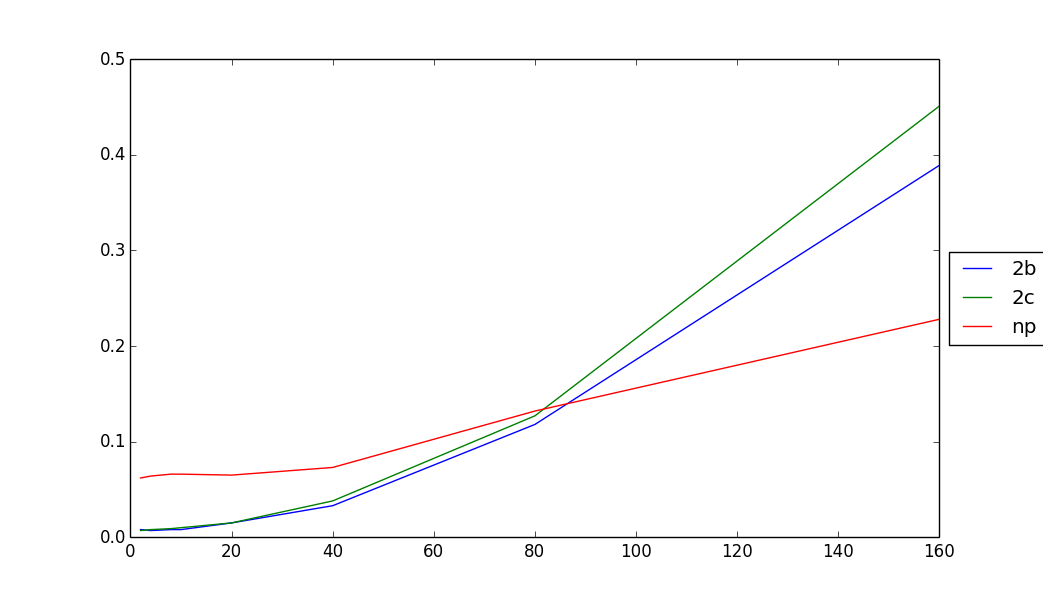
Результаты показывают, что:

• Версии функции numba превосходят цифровую версию для размеров матрицы до 80
• Версии Numba, кажется, масштабируются хуже, чем функция NumPy

Почему это? Есть ли какие-то накладные расходы, связанные с вызовом numpy, в отличие от вызова numba?

Почему цифровая функция лучше масштабируется? Делает ли он что-то причудливое с BLAS в фоновом режиме или использует превосходный алгоритм для расчета?

Могу ли я сделать шкалу функции Numba так же, как функцию NUMPY?