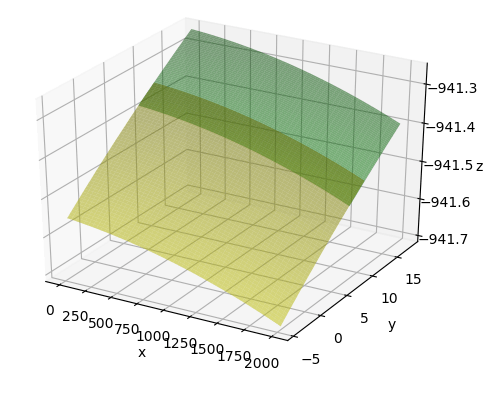
Найти уравнение y = y(x) от пересечения двух поверхностей z = z(x,y)
Учитывая уравнение z = z(x,y) из 2 поверхностей I а также II:
z_I(x, y) = a0 + a1*y + a2*x + a3*y**2 + a4*x**2 + a5*x*y
z_II(x, y) = a0_s2 + a1_s2*y + a2_s2*x + a3_s2*y**2 + a4_s2*x**2 + a5_s2*x*y
Параметры приведены в коде (ниже).
Пересечение обеих поверхностей выполняется, когда:
z_I(x, y) = z_II(x, y)
Как я мог найти уравнение y=y(x) для этого пересечения?
Код:
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
import matplotlib
import matplotlib.pyplot as plt
# parameters:
a0 = -941.487789748
a1 = 0.014688246093
a2 = -2.53546607894e-05
a3 = -9.6435353414e-05
a4 = -2.47408356408e-08
a5 = 3.77057147803e-07
a0_s2 = -941.483110904
a1_s2 = 0.01381970471
a2_s2 = -2.63051565187e-05
a3_s2 = -5.5529184524e-05
a4_s2 = -2.46707082089e-08
a5_s2 = 3.50929634874e-07
print """
The equations are the following:
z_I (x, y) = a0 + a1*y + a2*x + a3*y**2 + a4*x**2 + a5*x*y
z_II (x, y) = a0_s2 + a1_s2*y + a2_s2*x + a3_s2*y**2 + a4_s2*x**2 + a5_s2*x*y
"""
print('z_I (x, y) = ({a0}) + ({a1})*y + ({a2})*x ({a3})*y**2 ({a4})*x**2 + ({a5})*x*y'.format(a0 = a0, a1 = a1, a2 = a2, a3 = a3, a4 = a4, a5 = a5))
print """
"""
print('z_II (x, y) = ({a0_s2}) + ({a1_s2})*y + ({a2_s2})*x ({a3_s2})*y**2 ({a4_s2})*x**2 + ({a5_s2})*x*y'.format(a0_s2 = a0_s2, a1_s2 = a1_s2, a2_s2 = a2_s2, a3_s2 = a3_s2, a4_s2 = a4_s2, a5_s2 = a5_s2))
print """
"""
print """
The intersection of both surfaces is satisfied when:
z_I(x, y) = z_II(x, y)
In other words, I am looking for the expression of the function y=y(x)
"""
##### For plotting:
x_mesh = np.linspace(10.0000000000000, 2000.0000000000000, 200)
x_mesh_2 = np.linspace(10.0000000000000, 2000.0000000000000, 200)
print x_mesh[0]
print x_mesh[-1]
y_mesh = np.linspace(-4.4121040129800, 10.8555489379000, 200)
y_mesh_2 = np.linspace(8.0622039627300, 17.6458151433000, 200)
print y_mesh[0]
print y_mesh[-1]
xx, yy = np.meshgrid(x_mesh, y_mesh)
xx_2, yy_2 = np.meshgrid(x_mesh_2, y_mesh_2)
z_fit = a0 + a1*yy + a2*xx + a3*yy**2 + a4*xx**2 + a5*xx*yy
z_fit_2 = a0_s2 + a1_s2*yy_2 + a2_s2*xx_2 + a3_s2*yy_2**2 + a4_s2*xx_2**2 + a5_s2*xx_2*yy_2
# set "fig" and "ax" varaibles
fig = plt.figure()
ax = fig.gca(projection='3d')
# Plot the original function
ax.plot_surface(xx, yy, z_fit, color='y', alpha=0.5)
ax.plot_surface(xx_2, yy_2, z_fit_2, color='g', alpha=0.5)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('\nz', linespacing=3)
plt.show()
РЕДАКТИРОВАТЬ
Как указал @Alex, получено 2 решения, т.е. две поверхности пересекаются, образуя 2 кривые:
Если вы запустите приведенный ниже код, они получаются в sol:
sol = sym.solve(z_I(x,y) - z_II(x,y), y)
Теперь, если мы построим эти две кривые (все это в коде ниже), мы найдем эти две ветви:
Я понял, что это верно в ситуации, когда одна поверхность, т. Е. Зеленая, лежит поверх красно-желтой для области x а также y:
Я хотел бы найти пересечение между этими двумя ветвями (синий и оранжевый на 2D-графике).
Согласно тому, что обсуждалось, это может быть сделано sym.solve тоже:
cross = sym.solve(y_sol_z_I_sym(x) - y_sol_z_II_sym(x), x)
Однако это утверждение не работает с sym.sqrt (так и должно быть, поскольку квадратный корень считается символическим...)
Знаете ли вы, где проблема?
Код:
import numpy as np
import sympy as sym
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
a0 = -941.487789748
a1 = 0.014688246093
a2 = -2.53546607894e-05
a3 = -9.6435353414e-05
a4 = -2.47408356408e-08
a5 = 3.77057147803e-07
a0_s2 = -941.483110904
a1_s2 = 0.01381970471
a2_s2 = -2.63051565187e-05
a3_s2 = -5.5529184524e-05
a4_s2 = -2.46707082089e-08
a5_s2 = 3.50929634874e-07
x, y = sym.symbols('x y', real=True)
def z_I(x,y):
return a0 + a1*y + a2*x + a3*y**2 + a4*x**2 + a5*x*y
def z_II(x,y):
return a0_s2 + a1_s2*y + a2_s2*x + a3_s2*y**2 + a4_s2*x**2 + a5_s2*x*y
sol = sym.solve(z_I(x,y) - z_II(x,y), y)
print 'sol =', sol
# For obtaining the plot of the two branches y=y(x), we need np.sqrt
def y_sol_z_I(x):
return 0.000319359080035813*x - 1.22230952828787e-15*np.sqrt(-1.07919313606384e+24*x**2 + 2.00910207755286e+28*x - 1.12101975048632e+30) + 10.6162640815323
def y_sol_z_II(x):
return 0.000319359080035813*x + 1.22230952828787e-15*np.sqrt(-1.07919313606384e+24*x**2 + 2.00910207755286e+28*x - 1.12101975048632e+30) + 10.6162640815323
# For obtaining where the two branches y=y(x) intersect, we need sym.sqrt
def y_sol_z_I_sym(x):
return 0.000319359080035813*x - 1.22230952828787e-15*sym.sqrt(-1.07919313606384e+24*x**2 + 2.00910207755286e+28*x - 1.12101975048632e+30) + 10.6162640815323
def y_sol_z_II_sym(x):
return 0.000319359080035813*x + 1.22230952828787e-15*sym.sqrt(-1.07919313606384e+24*x**2 + 2.00910207755286e+28*x - 1.12101975048632e+30) + 10.6162640815323
cross = sym.solve(y_sol_z_I_sym(x) - y_sol_z_II_sym(x), x)
print ' cross = ', cross
##### Plotting:
# set "fig" and "ax" varaibles
fig = plt.figure()
ax = fig.gca(projection='3d')
# Plot the original function:
x_mesh = np.linspace(10.0000000000000, 2000.0000000000000, 20)
x_mesh_2 = np.linspace(10.0000000000000, 2000.0000000000000, 20)
print x_mesh[0]
print x_mesh[-1]
y_mesh = np.linspace(-4.4121040129800, 10.8555489379000, 20)
y_mesh_2 = np.linspace(8.0622039627300, 17.6458151433000, 20)
print y_mesh[0]
print y_mesh[-1]
xx, yy = np.meshgrid(x_mesh, y_mesh)
xx_2, yy_2 = np.meshgrid(x_mesh_2, y_mesh_2)
ax.plot_surface(xx, yy, z_I(xx ,yy), color='y', alpha=0.5)
ax.plot_surface(xx_2, yy_2, z_II(xx_2, yy_2), color='g', alpha=0.5)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('\n z, linespacing=3')
# New figure for the y=y(x) function:
fig = plt.figure()
x = np.linspace(10.0, 2000.0, 10000)
plt.plot(x, y_sol_z_I(x))
plt.plot(x, y_sol_z_II(x))
plt.xlabel('x')
plt.ylabel('y')
plt.title('Exact expression of y=y(x)\nas a result of making $z^{I}(x,y)=z^{II}(x,y)$')
tics_shown = [10, 250, 500, 750, 1000, 1250, 1500, 1750, 2000, 2250]
plt.xticks(tics_shown)
plt.grid()
# New figure for the y=y(x) function in circle:
fig = plt.figure()
x_circle = np.linspace(10.0, 2000.0*100, 10000*100)
plt.plot(x_circle, y_sol_z_I(x_circle))
plt.plot(x_circle, y_sol_z_II(x_circle))
plt.xlabel('x')
plt.ylabel('y')
plt.title('Exact expression of y=y(x)\nas a result of making $z^{I}(x,y)=z^{II}(x,y)$')
plt.grid()
plt.show()
1 ответ
Поскольку вы ищете символическое решение (в отличие от числового), вам нужна библиотека для символьных манипуляций, такая как SymPy.
import sympy as sym
x, y = sym.symbols('x y', real=True)
z_I = a0 + a1*y + a2*x + a3*y**2 + a4*x**2 + a5*x*y
z_II = a0_s2 + a1_s2*y + a2_s2*x + a3_s2*y**2 + a4_s2*x**2 + a5_s2*x*y
sol = sym.solve(z_I-z_II, y)
Массив sol содержит два решения, что не является чем-то необычным для квадратных уравнений.
[0.000319359080035813*x - 1.22230952828787e-15*sqrt(-1.07919313606384e+24*x**2 + 2.00910207755286e+28*x - 1.12101975048632e+30) + 10.6162640815323,
0.000319359080035813*x + 1.22230952828787e-15*sqrt(-1.07919313606384e+24*x**2 + 2.00910207755286e+28*x - 1.12101975048632e+30) + 10.6162640815323]
Если вы хотите найти, где они встречаются, используйте
cross = sym.solve(sol[0]-sol[1])
который возвращается [55.9652951064934, 18560.7401898885], х-координаты точек пересечения.