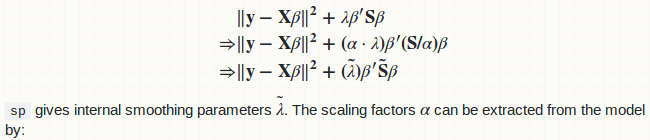mgcv: как вернуть расчетный параметр сглаживания?

Question

Рассмотрим простую подгонку GAM, как показано ниже:

library(mgcv)
my.gam <- gam(y~s(x), data=mydata)

1. Есть ли способ вернуть оценочный параметр сглаживания (лямбда), чтобы я мог его сохранить? Я знаю, что лямбда указывается в выходных данных как "оценка GCV", но мне нужен определенный код для ее возврата.
2. Как я могу установить лямбда на желаемое значение?

Answer 1

summary() не возвращает параметры сглаживания. Вы перепутали оценку GCV с параметром сглаживания. Обратитесь к местному статистику, если вы не понимаете этих концепций, или задайте вопрос о перекрестной проверке. Я только покажу вам, как извлечь и установить параметры сглаживания.

Рассмотрим пример:

library(mgcv)
set.seed(2)
dat <- gamSim(1, n=400, dist="normal", scale=2)
b <- gam(y ~ s(x0) + s(x1) + s(x2) + s(x3), data=dat)

Вы можете получить параметры внутреннего сглаживания из:

b$sp
#       s(x0)        s(x1)        s(x2)        s(x3) 
#3.648590e+00 3.850127e+00 1.252710e-02 4.986399e+10 

Но это не lambda, Они отличаются от lambda некоторыми положительными масштабными коэффициентами. Обычно достаточно использовать sp для сглаживания параметров. Если вы хотите установить фиксированное значение, сделайте, например:

b1 <- gam(y ~ s(x0, sp = 0) + s(x1, sp = 0) + s(x2, sp = 0) + s(x3, sp = 0),
          data = dat)

Это по существу отключает штраф за все гладкие условия. Обратите внимание, что настройка sp отрицательное значение подразумевает автоматический выбор sp,

---

lambdaа такжеsp:

sapply(b$smooth, "[[", "S.scale") / b$sp
#       s(x0)        s(x1)        s(x2)        s(x3) 
#6.545005e+00 5.326938e+00 1.490702e+03 4.097379e-10 

Иногда получая lambda является необходимым. При рассмотрении гладких функций как случайных эффектов или случайных полей, есть

variance_parameter_of_random_effect = scale_parameter / lambda

где параметр масштаба находится в b$scale (для гауссовой модели это также b$sig2). См. Связанный вопрос: GAM с "gp" smoother: как получить параметры вариограммы?

---

Следовать за

Да, мне нужно точное значение lambdaтак что спасибо за аккуратный код. Тем не менее мне интересно узнать больше о коэффициенте масштабирования. Где я могу прочитать больше об этом в дополнение к руководству по упаковке?

Читайте дальше ?smoothCon:

smoothCon(object,data,knots=NULL,absorb.cons=FALSE,
          scale.penalty=TRUE,n=nrow(data),dataX=NULL,
          null.space.penalty=FALSE,sparse.cons=0,
          diagonal.penalty=FALSE,apply.by=TRUE,modCon=0)

scale.penalty: should the penalty coefficient matrix be scaled to have
          approximately the same 'size' as the inner product of the
          terms model matrix with itself? ...

В исходном коде smoothCon, есть:

if (scale.penalty && length(sm$S) > 0 && is.null(sm$no.rescale)) {
    maXX <- norm(sm$X, type = "I")^2
    for (i in 1:length(sm$S)) {
        maS <- norm(sm$S[[i]])/maXX
        sm$S[[i]] <- sm$S[[i]]/maS
        sm$S.scale[i] <- maS
    }
}

Кратко говоря, для модельной матрицы X и сырая штрафная матрица S, коэффициент масштабирования maS является:

norm(S) / norm(X, type = "I")^2