Как мне сгенерировать равномерное распределение журналов в Python?

Я не смог найти встроенную функцию в Python для генерации равномерного распределения журнала, учитывая минимальное и максимальное значение ( здесь есть эквивалент R), что-то вроде: loguni[n, exp(min), exp(max), base] который возвращает n log, равномерно распределенный в диапазоне exp (min) и exp(max).

Самый близкий, который я нашел, был numpy.random.uniform,

Источник

3 ответа

Решение

От http://ecolego.facilia.se/ecolego/show/Log-Uniform%20Distribution:

В логуниформном распределении логтрансформированная случайная величина считается равномерно распределенной.

таким образом

logU(a, b) ~ exp(U(log(a), log(b))

Таким образом, мы могли бы создать равномерно распределенный журнал, используя numpy:

def loguniform(low=0, high=1, size=None):
    return np.exp(np.random.uniform(low, high, size))

Если вы хотите выбрать другую базу, мы могли бы определить новую функцию следующим образом:

def lognuniform(low=0, high=1, size=None, base=np.e):
    return np.power(base, np.random.uniform(low, high, size))
Источник

SciPy v1.4 включает loguniformслучайная переменная: https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.loguniform.html

Вот как им пользоваться:

from scipy.stats import loguniform

rvs = loguniform.rvs(1e-2, 1e0, size=1000)

Это создаст случайные переменные, равномерно распределенные между 0,01 и 1. Это лучше всего показано путем визуализации гистограммы с логарифмической шкалой:

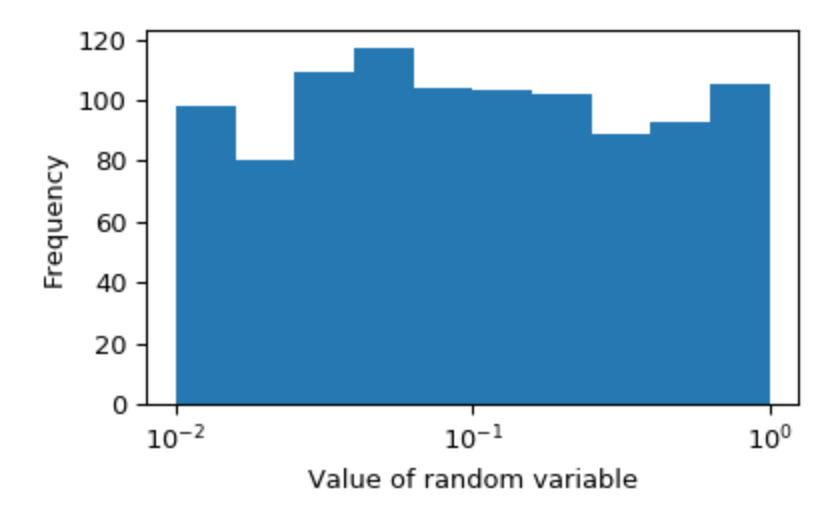
Это "масштабирование журнала" работает независимо от базы; loguniform.rvs(2**-2, 2**0, size=1000)также производит логарифмически однородные случайные величины. Более подробная информация вloguniformдокументацию.

Источник

Я верю scipy.stats.reciprocal это распределение, которое вы хотите.
Из документации:

Функция плотности вероятности для обратной:

f(x, a, b) = \frac{1}{x \log(b/a)}

для a <= x <= b и a, b > 0

взаимные взятия a а также b в качестве параметров формы.

Источник

Вот один из них:

Просто используйте .rvs() предоставленный метод:

class LogUniform(HyperparameterDistribution):
    """Get a LogUniform distribution.
    For example, this is good for neural networks' learning rates: that vary exponentially."""

    def __init__(self, min_included: float, max_included: float):
        """
        Create a quantized random log uniform distribution.
        A random float between the two values inclusively will be returned.
        :param min_included: minimum integer, should be somehow included.
        :param max_included: maximum integer, should be somehow included.
        """
        self.log2_min_included = math.log2(min_included)
        self.log2_max_included = math.log2(max_included)
        super(LogUniform, self).__init__()

    def rvs(self) -> float:
        """
        Will return a float value in the specified range as specified at creation.
        :return: a float.
        """
        return 2 ** random.uniform(self.log2_min_included, self.log2_max_included)

    def narrow_space_from_best_guess(self, best_guess, kept_space_ratio: float = 0.5) -> HyperparameterDistribution:
        """
        Will narrow, in log space, the distribution towards the new best_guess.
        :param best_guess: the value towards which we want to narrow down the space. Should be between 0.0 and 1.0.
        :param kept_space_ratio: what proportion of the space is kept. Default is to keep half the space (0.5).
        :return: a new HyperparameterDistribution that has been narrowed down.
        """
        log2_best_guess = math.log2(best_guess)
        lost_space_ratio = 1.0 - kept_space_ratio
        new_min_included = self.log2_min_included * kept_space_ratio + log2_best_guess * lost_space_ratio
        new_max_included = self.log2_max_included * kept_space_ratio + log2_best_guess * lost_space_ratio
        if new_max_included <= new_min_included or kept_space_ratio == 0.0:
            return FixedHyperparameter(best_guess).was_narrowed_from(kept_space_ratio, self)
        return LogUniform(2 ** new_min_included, 2 ** new_max_included).was_narrowed_from(kept_space_ratio, self)

Исходный проект также включает дистрибутив LogNormal, если это вас тоже интересует.

Источник:

Лицензия:

  • Лицензия Apache 2.0, авторское право Neuraxio Inc., 2019.
Источник 
from random import random
from math import log

def loguniform(lo,hi,seed=random()):
    return lo ** ((((log(hi) / log(lo)) - 1) * seed) + 1)

Вы можете проверить это, используя определенное начальное значение: lognorm(10,1000,0.5) возвращается 100.0

Источник

Лучшим подходом было бы вместо того, чтобы напрямую генерировать образец из логарифмической формы, вы должны создать логарифмическую однородную плотность.

В статистике говорят, что это обратное распределение, которое уже есть в SciPy: scipy.stats.reciprocal. Например, чтобы построить образец, который10^{x~U[-1,1]}, вы бы сделали:

rv = scipy.stats.reciprocal(a=0.1,b=10)
x = rv.rvs(N)

В качестве альтернативы я написал и использовал следующий код для преобразования журнала любого scipy.stats-подобная (замороженная) случайная величина

class LogTransformRV(scipy.stats.rv_continuous):
    def __init__(self,rv,base=10):
        self.rv = rv
        self.base = np.e if base in {'e','E'} else base
        super(LogTransformRV, self).__init__()
        self.a,self.b = self.base ** self.rv.ppf([0,1])

    def _pdf(self,x):
        return self.rv.pdf(self._log(x))/(x*np.log(self.base)) # Chain rule

    def _cdf(self,x):
        return self.rv.cdf(self._log(x)) 

    def _ppf(self,y):
        return self.base ** self.rv.ppf(y)

    def _log(self,x):
        return np.log(x)/np.log(self.base)
Источник 
from neuraxle.hyperparams.distributions import LogUniform

# Create a Log Uniform Distribution that ranges from 0.001 to 0.1: 
learning_rate_distribution = LogUniform(0.001, 0.1)

# Get a Random Value Sample (RVS) from the distribution: 
learning_rate_sample = learning_rate_distribution.rvs()

print(learning_rate_sample)

Пример вывода:

0,004532

Это использует Neuraxle.

Источник
Другие вопросы по тегам