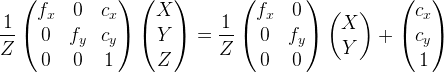Внутренние параметры 3D-реконструкции и SfM-камеры

Question

Я пытаюсь понять основные принципы 3D-реконструкции и решил поиграть с OpenMVG. Однако я видел доказательства того, что следующие концепции, о которых я спрашиваю, применимы ко всем / большинству инструментов SfM/MVS, а не только к OpenMVG. Поэтому я подозреваю, что любой инженер Computer Vision должен быть в состоянии ответить на эти вопросы, даже если у них нет прямого опыта работы с OpenMVG.

---

Я пытаюсь полностью понять внутренние параметры камеры, или, как они, кажется, называются, " внутренние характеристики камеры " или " внутренние параметры ". Согласно документации OpenMVG, характеристики камеры зависят от типа камеры, которая используется для съемки (например, модель камеры), из которых OpenMVG поддерживает пять моделей:

• Пинхол: 3 внутренних параметра (фокус, главная точка x, главная точка y)
• Радиус обскуры 1: 4 собственных параметра (фокус, главная точка x, главная точка y, один коэффициент радиального искажения)
• Радиус обскуры 3: 6 параметров (фокус, главная точка x, главная точка y, 3 радиальных коэффициента искажения)
• Пинхол Браун: 8 параметров (фокус, главная точка x, главная точка y, 5 коэффициентов искажения (3 радиальных +2 тангенциальных))
• Пинхол с искажением "рыбий глаз": 7 параметров (фокус, главная точка x, главная точка y, 4 фактора искажения)

Все это объясняется на их вики-странице, которая объясняет модель их камеры, которая является предметом моего вопроса.

На этой странице есть несколько основных концепций, которые мне необходимо прояснить:

• Фокальная плоскость: что это такое и чем оно отличается от плоскости изображения (как показано на диаграмме в верхней части этой страницы)?
• фокусное расстояние / длина: что это?
• Принципиальный момент: что это такое и почему он должен быть в идеале центром изображения?
• масштабный коэффициент: это только оценка того, как далеко камера находится от плоскости изображения?
• искажение: что это такое и в чем разница между его различными подтипами:
  • радиальный
  • тангенциальный
  • рыбий глаз

Заранее спасибо за любые уточнения / исправления здесь!

Answer 1

Я не уверен насчет фокальной плоскости, поэтому вернусь к ней после того, как напишу о других концепциях, которые вы упомянули. Предположим, у вас есть модель камеры с точечным отверстием с прямоугольными пикселями, и пусть P=[X Y Z]^T будет точкой в ​​пространстве камеры, где ^ T обозначает транспонирование. В этом случае (если Z - ось камеры), эту точку можно спроецировать как p=KP, где K (калибровочная матрица)

f_x  0   c_x
0   f_y  c_y
0    0    1 

(конечно, после этого вы захотите разделить p на третью координату).

Фокусное расстояние, которое я отмечу f - это расстояние между центром камеры и плоскостью изображения. Переменные

f_x=s_x*f 
f_y=s_y*f

в приведенной выше матрице соответственно выразите это значение в терминах ширины и высоты пикселя. Переменные s_x и s_y являются масштабными коэффициентами, которые упоминаются на цитируемой вами странице. Коэффициент масштабирования - это соотношение между размером (шириной или высотой) пикселей и единицами измерения, которые вы используете в пространстве камеры. Так, например, если ширина вашего пикселя составляет половину размера единиц, которые вы используете на оси x пространства камеры, у вас будет s_x = 2.

Я видел, как люди используют термин " главная точка" для обозначения разных вещей. В то время как некоторые люди определяют это как пересечение между осью камеры и плоскостью изображения (кажется, это делает Википедия), другие определяют это как точку, заданную [c_x c_y] ^ T. Для ясности давайте разделим весь процесс проецирования:

Два члена в правой части уравнения делают разные вещи. Первый масштабирует точку и помещает ее в плоскость изображения. Второй член (то есть [c_x c_y 1] ^ T) сдвигает результат от другого члена. Итак, [-c_x, -c_y] ^ T является центром системы координат изображения.

Что касается разницы между тангенциальным / радиальным искажением: обычно при коррекции искажения мы предполагаем, что центр изображения o остается неискаженным. Пиксель p будет "сдвинут" из своего истинного положения q под действием искажения. Если это движение происходит вдоль вектора qo, тогда искажение является радиальным, но если это движение имеет компонент в другом направлении, говорят, что оно (также) имеет тангенциальное искажение.

Как я уже сказал, я немного не уверен в том, что означает фокальная плоскость, которую они показывают на своей фигуре, но я думаю, что термин обычно относится к плоскости, в которой перевернутое изображение будет формироваться в физической камере с точечным отверстием. Точка P на плоскости изображения (выраженная в мировых координатах) будет просто -P на фокальной плоскости.