Кривая подгонки уравнений Python

Question

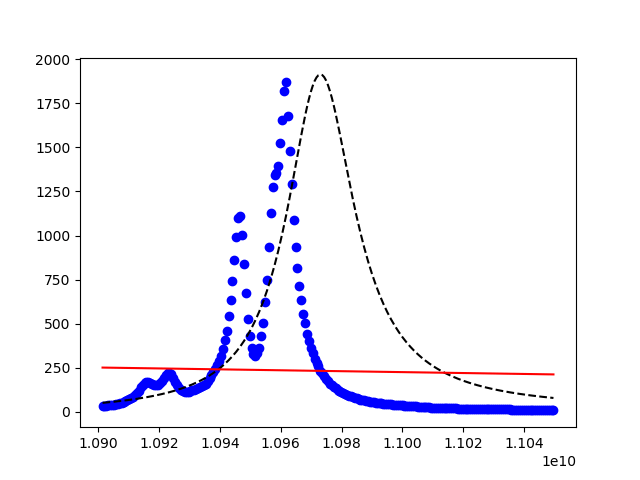
Я пытаюсь согласовать данные с уравнением допуска для цепи rlc, имеющей 6 компонентов. Я следую примеру, учитывая, что он [подходит] 1 раз и вставил мое уравнение. Уравнение является действительной частью допуска для 6-компонентной схемы, упрощенной с помощью Mathcad. На прилагаемом рисунке ось x является омега (w=2*pi*f), а y - входной сигнал в миллисименсах.

Программа работает, но не подходит, несмотря на хорошую пробную функцию. Я ценю любую помощь, почему посадка прямая. Я приложил также пример гауссовской подгонки.

это то, что я получаю, когда пытаюсь соответствовать уравнению. Данные с меньшим пиком слева, а пробная функция - пунктирная линия. подгонка прямая

from numpy import sqrt, pi, exp, linspace, loadtxt
from lmfit import  Model

import matplotlib.pyplot as plt

data = loadtxt("C:/Users/susu/circuit_eq_real5.dat")
x = data[:, 0]
y = data[:, 1]

def circuit(x,C0,Cm,Lm,Rm,R0,Rs):


    return ((C0**2*Cm**2*Lm**2*R0*x**4)+(Rs*C0**2*Cm**2*Lm**2*x**4)+(C0**2*Cm**2*R0**2*Rm*x**2)+(Rs*C0**2*Cm**2*R0**2*x**2)+(C0**2*Cm**2*R0*Rm**2*x**2)+(2*Rs*C0**2*Cm**2*R0*Rm*x**2)+(Rs*C0**2*Cm**2*Rm**2*x**2)-(2*C0**2*Cm*Lm*R0*x**2)-(2*Rs*C0**2*Cm*Lm*x**2)+(C0**2*R0)+(Rs*C0**2)-(2*Rs*C0*Cm**2*Lm*x**2)+(2*Rs*C0*Cm)+(Cm**2*Rm)+(Rs*Cm**2))/((C0**2*Cm**2*Lm**2*x**4)+(C0**2*Cm**2*R0**2*x**2)+(2*C0**2*Cm**2*R0*Rm*x**2)+(C0**2*Cm**2*Rm**2*x**2)-(2*C0**2*Cm*Lm*x**2)+(C0**2)-(2*C0*Cm**2*Lm*x**2)+(2*C0*Cm)+(Cm**2))

gmodel = Model(circuit)
result = gmodel.fit(y, x=x, C0=1.0408*10**(-12), Cm=5.953*10**(-14), 
Lm=1.475*10**(-7), Rm=1.571, R0=2.44088, Rs=0.42)

print(result.fit_report())

plt.plot(x, y,         'bo')
plt.plot(x, result.init_fit, 'k--')
plt.plot(x, result.best_fit, 'r-')
plt.show()

Ниже приведен отчет о пригодности

 [[Fit Statistics]]
# fitting method   = leastsq
# function evals   = 14005
# data points      = 237
# variables        = 6
chi-square         = 32134074.5
reduced chi-square = 139108.548
Akaike info crit   = 2812.71607
Bayesian info crit = 2833.52443
[[Variables]]
C0: -7.5344e-15 +/- 6.3081e-09 (83723736.65%) (init = 1.0408e-12)
Cm: -8.9529e-13 +/- 1.4518e-06 (162164237.47%) (init = 5.953e-14)
Lm:  2.4263e-06 +/- 1.94051104 (79978205.20%) (init = 1.475e-07)
Rm: -557.974399 +/- 1.3689e+09 (245334051.75%) (init = 1.571)
R0: -5178.53517 +/- 6.7885e+08 (13108904.45%) (init = 2.44088)
Rs:  2697.67659 +/- 7.3197e+08 (27133477.70%) (init = 0.42)
[[Correlations]] (unreported correlations are < 0.100)
C(R0, Rs) = -1.003
C(Rm, Rs) = -0.987
C(Rm, R0) =  0.973
C(C0, Lm) =  0.952
C(C0, Cm) = -0.502
C(Cm, R0) = -0.483
C(Cm, Rs) =  0.453
C(Cm, Rm) = -0.388
C(Cm, Lm) = -0.349
C(C0, R0) =  0.310
C(C0, Rs) = -0.248
C(C0, Rm) =  0.148

Большое спасибо M Newville, Mikuszefski и другим за ваши идеи и отзывы. Я согласился с тем, что я поставил, возможно, в программе есть беспорядок. Из кода Python видно, что я не разбираюсь в Python или программировании.

Mikuszefsky, спасибо за размещение примера кода rlc. Ваш подход аккуратный и интересный. Я не знал, что Python выполняет прямую сложную подгонку. Я попробую ваш подход и посмотрим, сможет ли подойти. Я хочу соответствовать как реальной, так и мнимой части Y (допуск). Я обязательно где-нибудь застряну и опубликую свой прогресс здесь. Бест, Сусу

Answer 1

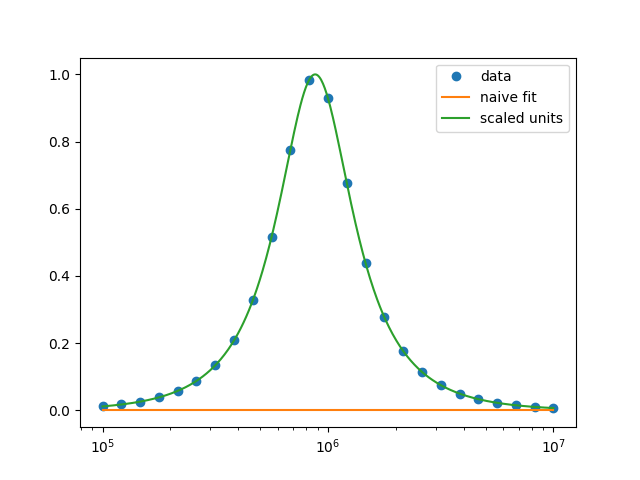
Вот способ очистки цепей RLC с параллельными и последовательными соединениями. Это позволяет избежать этой супер длинной очереди и трудно проверить функцию. Он также избегает Matlab или подобных программ, так как он непосредственно вычисляет схему. Конечно, это может быть легко расширено цепь OP. Как указывает М. Ньювилл, простая подгонка не удалась. Если, с другой стороны, единицы масштабируются до натуральных единиц, это работает даже без начальных параметров. Обратите внимание, что результаты корректны только по коэффициенту масштабирования. Нужно знать хотя бы одно значение компонентов.

import matplotlib.pyplot as plt
import numpy as np
from scipy.optimize import curve_fit

def r_l( w, l ):
    return 1j * w * l

def r_c( w, c ):
    return 1. / ( 1j * w * c )

def parallel( a, b ):
    return( 1. / ( 1./ a + 1. / b ) )

def series( a, b ):
    return a + b

# simple rlc band pass filter (to be extended)
def rlc_band( w , r, l, c ):
    lc = parallel( r_c( w , c ), r_l( w, l ) )
    return lc / series( r, lc )

def rlc_band_real( w , r, l, c ):
    return rlc_band( w , r, l, c ).real

def rlc_band_real_milli_nano( w , r, l, c ):
    return rlc_band_real( w , r, 1e-6 * l, 1e-9 * c ).real

wList = np.logspace( 5, 7, 25 )
wFullList = np.logspace( 5, 7, 500 )
rComplexList = np.fromiter( ( rlc_band(w, 12, 1.3e-5, 1e-7 ) for w in wList ), np.complex )
rList = np.fromiter( ( r.real for r in rComplexList ), np.float )
pList = np.fromiter( ( np.angle( r ) for r in rComplexList ), np.float )

fit1, pcov = curve_fit( rlc_band_real, wList, rList )
print fit1
print "does not work"

fit2, pcov = curve_fit( rlc_band_real_milli_nano, wList, rList )
print fit2
print "works, but is not unique (scaling is possible)"
print 12, fit2[1] * 12 / fit2[0], fit2[2] * fit2[0] / 12.

fig = plt.figure()
ax = fig.add_subplot( 1, 1, 1 )

ax.plot( wList, rList , ls='', marker='o', label='data')
#~ ax.plot( wList, pList )
ax.plot( wFullList, [ rlc_band_real( w , *fit1 ) for w in wFullList ], label='naive fit')
ax.plot( wFullList, [ rlc_band_real_milli_nano( w , *fit2 ) for w in wFullList ], label='scaled units')
ax.set_xscale('log')
ax.legend( loc=0 )

plt.show()

Обеспечение:

>> /...minpack.py:785: OptimizeWarning: Covariance of the parameters could not be estimated category=OptimizeWarning)
>> [1. 1. 1.]
>> does not work
>> [ 98.869924   107.10908434  12.13715912]
>> works, but is not unique (scaling is possible)
>> 12 13.0 100.0

Answer 2

Предоставление реальной ссылки на текстовый файл с фактическими данными, которые вы используете, и / или реальный сюжет того, что вы на самом деле видите, было бы наиболее полезным. Также, пожалуйста, предоставьте точное и полное описание результатов, включая текст того, что фактически распечатано print(result.fit_report()), По сути, спросите себя, как вы можете попытаться помочь кому-то, кто задал такой вопрос, и предоставьте как можно больше информации.

Никто (включая вас) никогда не сможет проверить правописание реализации вашей функции. Вам потребуется тщательное и тщательное тестирование этой функции, чтобы убедить кого-либо (включая вас, я надеюсь), что она делает то, что, по вашему мнению, должна делать. Вы должны предоставить результаты этих тестов, прежде чем беспокоиться о том, почему они не работают как подходящая функция. Вы должны определенно рассмотреть возможность преобразования этого беспорядка уравнения в более управляемые и удобочитаемые части.

Тем не менее, я также настоятельно рекомендую, чтобы вы работали не в единицах Фарада и Генри, а в picoFarads или nanoFarads и microHenrys. Это сделает значения намного ближе к 1 (скажем, порядка от 1e-6 до 1e+6), что облегчит подгонку для выполнения своей работы.