Оптимизированный wayfinder

Question

У меня довольно сложная проблема, и я постараюсь описать ее. Я не являюсь носителем английского языка, поэтому, если есть какие-либо сомнения по поводу того, что я имел в виду, спросите меня

Описание

Я борюсь с каким-то следопытом. У меня есть сетка со списком из N точек координат [x,y]. Вам нужно перейти из точки A в точку B, обе принадлежат к предыдущему списку. Вы можете перемещаться только между двумя существующими точками. Мне нужна функция, которая принимает в качестве параметров список точек, начальную точку A, конечную точку B и максимальное расстояние D.

Цель состоит в том, чтобы выяснить, можете ли вы перейти от А к В, используя промежуточные точки, не проходя больше расстояния D между двумя последовательными точками вашего пути. Если вы не можете, нам нужно найти минимальное расстояние D', которое следует правилу выше.

---

Пример: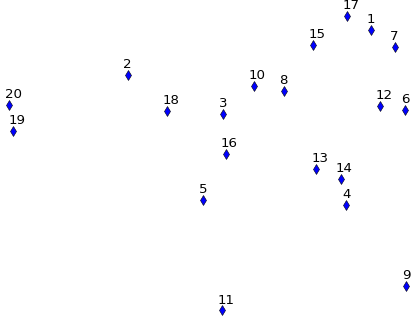

Чтобы перейти от точки 7 к точке 5 на этом графике, путь, который минимизирует максимальное расстояние, когда-либо проходившее между двумя точками, составляет 7 > 1 > 17 > 15 > 8 > 10 > 3 > 16 > 5

---

Решение

Я придумал решение этой проблемы с помощью Python. Однако, когда очков больше ста, мой сценарий страдает. Я действительно пытался оптимизировать это до максимума, уменьшая бесполезное воздействие на память и стараясь избегать бесполезных тестов, однако этого по-прежнему недостаточно. Есть ли у вас какие-либо идеи о том, как повысить его эффективность? Я думал попробовать рекурсивные методы, но не думаю, что это что-то изменит, так как это просто итеративный способ написания рекурсии. Любые советы приветствуются:)

Мое решение проблемы с использованием Python:

def OptimizedPath( a, b, points, Dmax ):
# Dmax is the maximal distance you can travel between two points
# D is a function which calculate the distance between two points
maxi = D( points[a], points[b])
if maxi < Dmax: # if the direct travel is already ok
    return Dmax
else:
    ways = [[a]]    # itervative methode to explore all paths
    while ways != []:
        nways = []  # new matrix that will contain all paths of n+1 points
        for w in ways:
            # PAcc returns the list of points you can access in less than a distance maxi
            for i in PAcc( w, maxi, points):
                nways.append( w + [i] )

        ways = []
        for w in nways:
            if w[-1] == b:  # if a path has arrived to it's destination
                if Dmaxw( w, points ) < Dmax:   # if it has done it without traveling more than Dmax between two points
                    return Dmax
                elif Dmaxw( w, points ) < maxi: # if it has done it better than the best path found
                    maxi = Dmaxw( w, points )
            elif Dmaxw( w, points ) < maxi: # if it's not over and the maximum distance between two points is smaller than maxi
                ways.append( w )
    return maxi

Answer 1

Относитесь к вашей сетке как Graphкаждая точка как vertex, Найти расстояние между каждой парой вершин, а затем вы можете найти минимальное расстояние между точками A в B используя алгоритм Дейкстры (алгоритм кратчайшего пути из одного источника). Хотя сложность времени останется O(n^2) так как вам нужно сначала найти расстояние между каждой парой вершин.

Answer 2

Все в порядке,

Я хочу поблагодарить вас всех, но в конце концов алгоритм Дейкстры все решил. У меня были проблемы с адаптацией к этой конкретной проблеме, поскольку я впервые использовал этот продвинутый алгоритм оптимизации графиков, и я не хотел находить кратчайший путь, но максимальное расстояние между двумя точками. Наконец-то это сработало и принесло лучший результат (как по времени, так и по использованию памяти).

Решение моей проблемы с использованием Python

def nextc( A, U ):
    mini = A[U[0]][0]
    indice = U[0]
    for i in range(1,len(A)):
        if A[i][0] < mini and i in U:
            mini = A[i][0]
            indice = i
    return indice

def DijkstraS( s, e, points ):
    L = D( points[s], points[e] )
    U = [ x for x in range( len(points) ) ]
    A = [ [float('inf'), -1] for i in range(len(points))]
    A[s][0] = 0
    while U != []:
        current = nextc( A, U )
        U.remove(current)
        for P in U:
            Dt = D( points[P], points[current] )
            if Dt < L and max( Dt, A[current][0]) < A[P][0]:
                A[P][0] = max( Dt, A[current][0])
                A[P][1] = current
    return A[e][0]