Как нарисовать границы решения в SVM sklearn данных в Python?

Question

Я читаю данные электронной почты из учебного набора и создаю train_matrix, train_labels и test_labels. Теперь, как мне отобразить границу решения, используя matplot в python. Я использую SVM Sklearn. Есть онлайн пример для предварительно заданных наборов данных через радужную оболочку. Но заговор терпит неудачу на пользовательских данных. Вот мой код

Ошибка:

Traceback (most recent call last):
  File "classifier-plot.py", line 115, in <module>
    Z = Z.reshape(xx.shape)
ValueError: cannot reshape array of size 260 into shape (150,1750)

Код:

import os
import numpy as np
from collections import Counter
from sklearn import svm
import matplotlib
import matplotlib.pyplot as plt
from sklearn.metrics import accuracy_score


def make_Dictionary(root_dir):
    all_words = []
    emails = [os.path.join(root_dir,f) for f in os.listdir(root_dir)]
    for mail in emails:
        with open(mail) as m:
            for line in m:
                words = line.split()
                all_words += words
    dictionary = Counter(all_words)
    list_to_remove = dictionary.keys()

    for item in list_to_remove:
        if item.isalpha() == False:
            del dictionary[item]
        elif len(item) == 1:
            del dictionary[item]
    dictionary = dictionary.most_common(3000)

    return dictionary



def extract_features(mail_dir):
    files = [os.path.join(mail_dir,fi) for fi in os.listdir(mail_dir)]
    features_matrix = np.zeros((len(files),3000))
    train_labels = np.zeros(len(files))
    count = 0;
    docID = 0;
    for fil in files:
      with open(fil) as fi:
        for i,line in enumerate(fi):
          if i == 2:
            words = line.split()
            for word in words:
              wordID = 0
              for i,d in enumerate(dictionary):
                if d[0] == word:
                  wordID = i
                  features_matrix[docID,wordID] = words.count(word)
        train_labels[docID] = 0;
        filepathTokens = fil.split('/')
        lastToken = filepathTokens[len(filepathTokens) - 1]
        if lastToken.startswith("spmsg"):
            train_labels[docID] = 1;
            count = count + 1
        docID = docID + 1
    return features_matrix, train_labels



TRAIN_DIR = "../train-mails"
TEST_DIR = "../test-mails"

dictionary = make_Dictionary(TRAIN_DIR)

print "reading and processing emails from file."
features_matrix, labels = extract_features(TRAIN_DIR)
test_feature_matrix, test_labels = extract_features(TEST_DIR)


model = svm.SVC(kernel="rbf", C=10000)

print "Training model."
features_matrix = features_matrix[:len(features_matrix)/10]
labels = labels[:len(labels)/10]
#train model
model.fit(features_matrix, labels)

predicted_labels = model.predict(test_feature_matrix)

print "FINISHED classifying. accuracy score : "
print accuracy_score(test_labels, predicted_labels)







##----------------

h = .02  # step size in the mesh

# we create an instance of SVM and fit out data. We do not scale our
# data since we want to plot the support vectors
C = 1.0  # SVM regularization parameter
X = features_matrix
y = labels
svc = model.fit(X, y)
#svm.SVC(kernel='linear', C=C).fit(X, y)

# create a mesh to plot in
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = y[:].min() - 1, y[:].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                     np.arange(y_min, y_max, h))

# title for the plots
titles = ['SVC with linear kernel']



Z = predicted_labels#svc.predict(np.c_[xx.ravel(), yy.ravel()])

# Put the result into a color plot
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.coolwarm, alpha=0.8)

# Plot also the training points
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.coolwarm)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.xticks(())
plt.yticks(())
plt.title(titles[0])

plt.show()

Answer 1

В учебнике, который вы читали Z вычисляется путем применения классификатора к набору векторов признаков, сгенерированных для формирования регулярного NxM сетка. Это делает сюжет гладким.

Когда вы заменили

Z = svc.predict(np.c_[xx.ravel(), yy.ravel()])

с

Z = predicted_labels

вы заменили эту регулярную сетку на прогнозы, сделанные в вашем наборе данных. Следующая строка завершилась ошибкой, так как не смогла изменить размер массива len(files) для NxM матрица. Нет причины len(files) = NxM,

Есть причина, по которой вы не могли следовать учебнику напрямую. Ваше измерение данных равно 3000, поэтому границей вашего решения будет 2999-мерная гиперплоскость в 3000-мерном пространстве. Это не легко визуализировать.

В учебнике размер равен 4, а для визуализации он уменьшен до 2. Лучший способ уменьшить размерность ваших данных зависит от данных. В уроке мы просто выбираем первые два компонента 4-мерного вектора.

Другим вариантом, который хорошо работает во многих случаях, является использование анализа основных компонентов, чтобы уменьшить размерность данных.

from sklearn.decomposition import PCA
pca = PCA(n_components = 2)
pca.fit(features_matrix, labels)
reduced_matrix = pca.fit_transform(features_matrix, labels)
model.fit(reduced_matrix, labels)

Такая модель может быть использована для 2D визуализации. Вы можете просто следовать руководству и определить

Z = model.predict(np.c_[xx.ravel(), yy.ravel()])

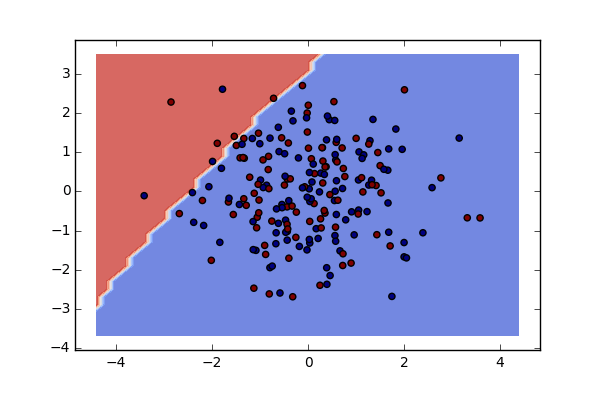
Полный, но не очень впечатляющий пример

У нас нет доступа к вашим данным электронной почты, поэтому для иллюстрации мы могли бы просто использовать случайные данные.

from sklearn import svm
from sklearn.decomposition import PCA

# initialize algorithms and data with random
model = svm.SVC(gamma=0.001,C=100.0)
pca = PCA(n_components = 2)
rng = np.random.RandomState(0)
U = rng.rand(200, 2000)
v = (rng.rand(200)*2).astype('int')
pca.fit(U,v)
U2 = pca.fit_transform(U,v)
model.fit(U2,v)

# generate grid for plotting
h = 0.2
x_min, x_max = U2[:,0].min() - 1, U2[:, 0].max() + 1
y_min, y_max = U2[:,1].min() - 1, U2[:, 1].max() + 1
xx, yy = np.meshgrid(
    np.arange(x_min, x_max, h),
    np.arange(y_min, y_max, h))

# create decision boundary plot
Z = s.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
contourf(xx,yy,Z,cmap=plt.cm.coolwarm, alpha=0.8)
scatter(U2[:,0],U2[:,1],c=v)
show()

Будет производить решение границы, которая выглядит не очень впечатляюще.

Действительно, первые два основных компонента охватывают только около 1% информации, содержащейся в данных

>>> print(pca.explained_variance_ratio_) 
[ 0.00841935  0.00831764]

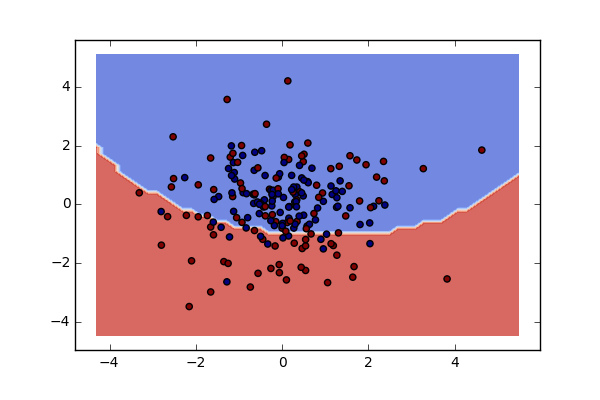
Если сейчас вы введете немного замаскированной асимметрии, вы уже увидите эффект.

Измените данные, чтобы ввести смещения только по одной координате, случайно выбранной для каждого объекта

random_shifts = (rng.rand(2000)*200).astype('int')
for i in range(MM):
    if v[i] == 1:
        U[i,random_shifts[i]] += 5.0

А применяя PCA, вы получите более информативную картину.

Обратите внимание, что здесь первые два основных компонента уже объясняют около 5% дисперсии, а красная часть изображения содержит гораздо больше красных точек, чем синих.