График загрузки PCA и загрузки в биплот в sklearn (как автоплот R)
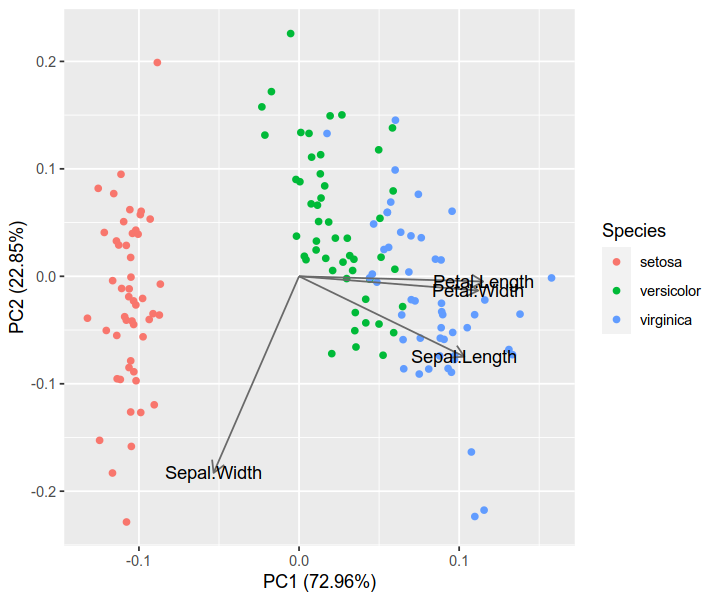
Я видел этот учебник в R ж / autoplot, Они наносили на карту загрузки и метки загрузки:
autoplot(prcomp(df), data = iris, colour = 'Species',
loadings = TRUE, loadings.colour = 'blue',
loadings.label = TRUE, loadings.label.size = 3)
 https://cran.r-project.org/web/packages/ggfortify/vignettes/plot_pca.html
https://cran.r-project.org/web/packages/ggfortify/vignettes/plot_pca.html
я предпочитаю Python 3 ж / matplotlib, scikit-learn, and pandas для моего анализа данных. Тем не менее, я не знаю, как добавить их?
Как вы можете построить эти векторы с matplotlib ?
Я читал Восстановление названий функций объясненных_вариантов_рассы в PCA с помощью sklearn, но пока не понял
Вот как я строю это в Python
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn import decomposition
import seaborn as sns; sns.set_style("whitegrid", {'axes.grid' : False})
%matplotlib inline
np.random.seed(0)
# Iris dataset
DF_data = pd.DataFrame(load_iris().data,
index = ["iris_%d" % i for i in range(load_iris().data.shape[0])],
columns = load_iris().feature_names)
Se_targets = pd.Series(load_iris().target,
index = ["iris_%d" % i for i in range(load_iris().data.shape[0])],
name = "Species")
# Scaling mean = 0, var = 1
DF_standard = pd.DataFrame(StandardScaler().fit_transform(DF_data),
index = DF_data.index,
columns = DF_data.columns)
# Sklearn for Principal Componenet Analysis
# Dims
m = DF_standard.shape[1]
K = 2
# PCA (How I tend to set it up)
Mod_PCA = decomposition.PCA(n_components=m)
DF_PCA = pd.DataFrame(Mod_PCA.fit_transform(DF_standard),
columns=["PC%d" % k for k in range(1,m + 1)]).iloc[:,:K]
# Color classes
color_list = [{0:"r",1:"g",2:"b"}[x] for x in Se_targets]
fig, ax = plt.subplots()
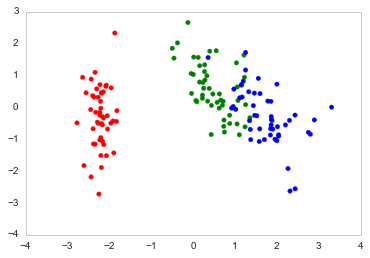
ax.scatter(x=DF_PCA["PC1"], y=DF_PCA["PC2"], color=color_list)
5 ответов
Вы можете сделать что-то вроде следующего, создав biplot функция. В этом примере я использую данные радужной оболочки:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.decomposition import PCA
import pandas as pd
from sklearn.preprocessing import StandardScaler
iris = datasets.load_iris()
X = iris.data
y = iris.target
#In general a good idea is to scale the data
scaler = StandardScaler()
scaler.fit(X)
X=scaler.transform(X)
pca = PCA()
x_new = pca.fit_transform(X)
def myplot(score,coeff,labels=None):
xs = score[:,0]
ys = score[:,1]
n = coeff.shape[0]
scalex = 1.0/(xs.max() - xs.min())
scaley = 1.0/(ys.max() - ys.min())
plt.scatter(xs * scalex,ys * scaley, c = y)
for i in range(n):
plt.arrow(0, 0, coeff[i,0], coeff[i,1],color = 'r',alpha = 0.5)
if labels is None:
plt.text(coeff[i,0]* 1.15, coeff[i,1] * 1.15, "Var"+str(i+1), color = 'g', ha = 'center', va = 'center')
else:
plt.text(coeff[i,0]* 1.15, coeff[i,1] * 1.15, labels[i], color = 'g', ha = 'center', va = 'center')
plt.xlim(-1,1)
plt.ylim(-1,1)
plt.xlabel("PC{}".format(1))
plt.ylabel("PC{}".format(2))
plt.grid()
#Call the function. Use only the 2 PCs.
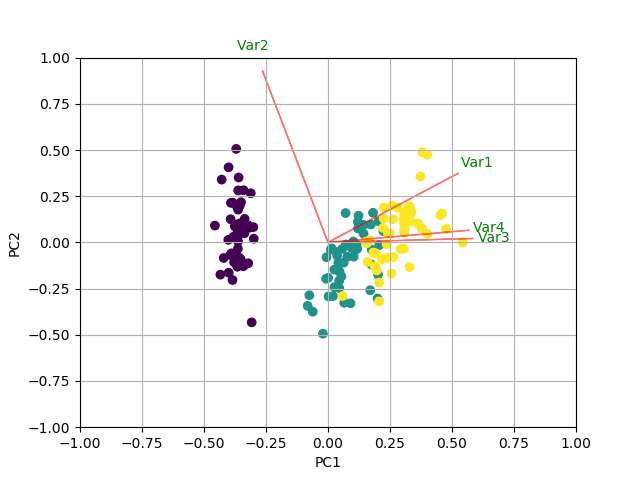
myplot(x_new[:,0:2],np.transpose(pca.components_[0:2, :]))
plt.show()
РЕЗУЛЬТАТ
Попробуйте библиотеку pca. Это будет отображать объясненную дисперсию и создать двойной график.
pip install pca
from pca import pca
# Initialize to reduce the data up to the number of componentes that explains 95% of the variance.
model = pca(n_components=0.95)
# Or reduce the data towards 2 PCs
model = pca(n_components=2)
# Fit transform
results = model.fit_transform(X)
# Plot explained variance
fig, ax = model.plot()
# Scatter first 2 PCs
fig, ax = model.scatter()
# Make biplot with the number of features
fig, ax = model.biplot(n_feat=4)
Я хотел бы добавить общее решение этой темы. После тщательного исследования существующих решений (включая Python и R) и наборов данных (особенно биологических «омических» наборов данных). Я нашел следующее решение Python, которое имеет следующие преимущества:
Масштабируйте оценки (выборки) и нагрузки (функции) должным образом, чтобы сделать их визуально приятными на одном графике. Следует отметить, что относительные масштабы выборок и признаков не имеют никакого математического значения (но имеют их относительные направления), однако придание им одинакового размера может облегчить исследование.
Может обрабатывать многомерные данные, где есть много функций, и можно было позволить визуализировать только несколько верхних функций (стрелки), которые управляют наибольшей дисперсией данных. Это включает в себя явный выбор и масштабирование основных функций.
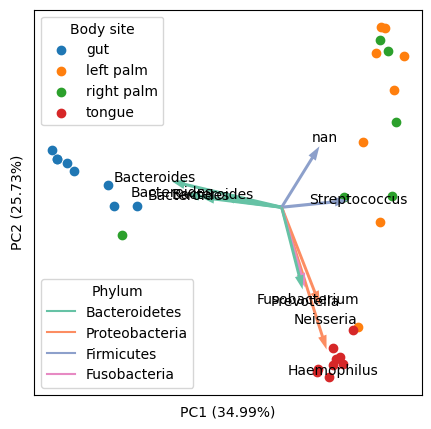
Пример конечного вывода (с использованием « Moving Pictures », классического набора данных в моей исследовательской области):
Подготовка:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
Базовый пример: отображение всех функций (стрелки)
Мы будем использовать набор данных iris (150 образцов по 4 признакам).
# load data
iris = datasets.load_iris()
X = iris.data
y = iris.target
targets = iris.target_names
features = iris.feature_names
# standardization
X_scaled = StandardScaler().fit_transform(X)
# PCA
pca = PCA(n_components=2).fit(X_scaled)
X_reduced = pca.transform(X_scaled)
# coordinates of samples (i.e., scores; let's take the first two axes)
scores = X_reduced[:, :2]
# coordinates of features (i.e., loadings; note the transpose)
loadings = pca.components_[:2].T
# proportions of variance explained by axes
pvars = pca.explained_variance_ratio_[:2] * 100
А вот и важная часть: правильно масштабируйте функции (стрелки), чтобы они соответствовали образцам (точкам). Следующий код масштабируется по максимальному абсолютному значению отсчетов по каждой оси.
arrows = loadings * np.abs(scores).max(axis=0)
Другой способ, как обсуждалось в ответе Сералоука, - масштабировать по диапазону (макс. - мин.). Но это сделает стрелки больше, чем точки.
# arrows = loadings * np.ptp(scores, axis=0)
Затем нарисуйте точки и стрелки:
plt.figure(figsize=(5, 5))
# samples as points
for i, name in enumerate(targets):
plt.scatter(*zip(*scores[y == i]), label=name)
plt.legend(title='Species')
# empirical formula to determine arrow width
width = -0.0075 * np.min([np.subtract(*plt.xlim()), np.subtract(*plt.ylim())])
# features as arrows
for i, arrow in enumerate(arrows):
plt.arrow(0, 0, *arrow, color='k', alpha=0.5, width=width, ec='none',
length_includes_head=True)
plt.text(*(arrow * 1.05), features[i],
ha='center', va='center')
# axis labels
for i, axis in enumerate('xy'):
getattr(plt, f'{axis}ticks')([])
getattr(plt, f'{axis}label')(f'PC{i + 1} ({pvars[i]:.2f}%)')
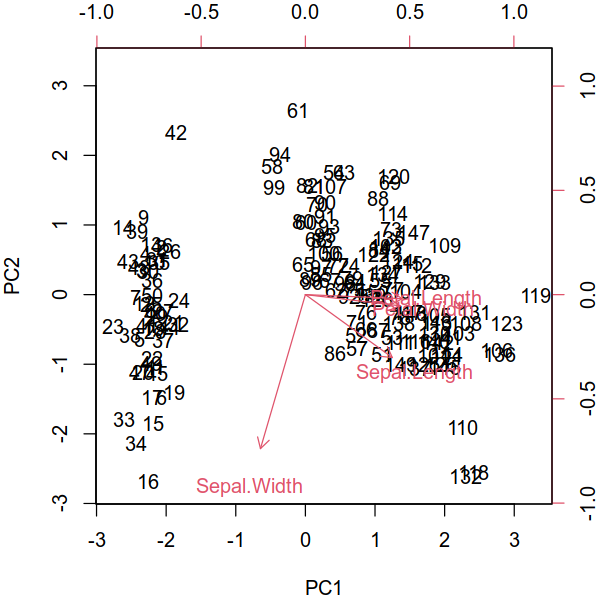
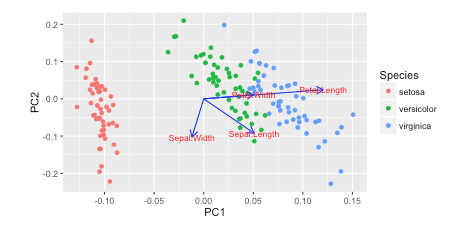
Сравните результат с раствором R. Вы можете видеть, что они вполне последовательны. (Примечание: известно, что PCA R и scikit-learn имеют противоположные оси. Вы можете перевернуть одну из них, чтобы сделать направления согласованными.)
iris.pca <- prcomp(iris[, 1:4], center = TRUE, scale. = TRUE)
biplot(iris.pca, scale = 0)
library(ggfortify)
autoplot(iris.pca, data = iris, colour = 'Species',
loadings = TRUE, loadings.colour = 'dimgrey',
loadings.label = TRUE, loadings.label.colour = 'black')
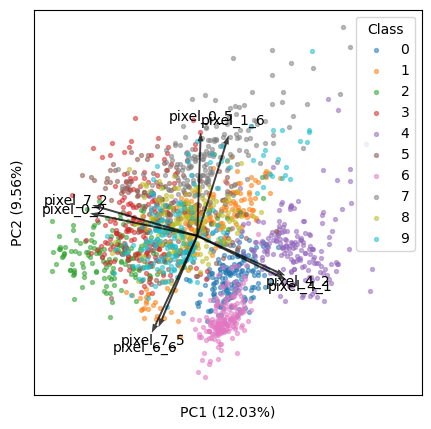
Расширенный пример: отображение только лучших k функций
Мы будем использовать набор данных digits (1797 образцов по 64 функциям).
# load data
digits = datasets.load_digits()
X = digits.data
y = digits.target
targets = digits.target_names
features = digits.feature_names
# analysis
X_scaled = StandardScaler().fit_transform(X)
pca = PCA(n_components=2).fit(X_scaled)
X_reduced = pca.transform(X_scaled)
# results
scores = X_reduced[:, :2]
loadings = pca.components_[:2].T
pvars = pca.explained_variance_ratio_[:2] * 100
Теперь мы найдем лучшие k функций, которые лучше всего объясняют наши данные.
k = 8
Метод 1: Найдите k верхних стрелок, которые кажутся самыми длинными (т. е. самыми удаленными от начала координат) на видимом графике:
- Обратите внимание, что все функции имеют одинаковую длину в пространстве m на m . Но они различны в пространстве 2 на m ( m — общее количество признаков), и следующий код должен найти самые длинные в последнем.
- Этот метод согласуется с программой микробиома QIIME 2/EMPeror ( исходный код).
tops = (loadings ** 2).sum(axis=1).argsort()[-k:]
arrows = loadings[tops]
Метод 2. Найдите лучшие k функций, которые вызывают наибольшую дисперсию среди видимых ПК:
# tops = (loadings * pvars).sum(axis=1).argsort()[-k:]
# arrows = loadings[tops]
Теперь возникает новая проблема: когда количество признаков велико, поскольку первые k признаков составляют лишь очень небольшую часть всех признаков, их вклад в дисперсию данных ничтожен, поэтому на графике они будут выглядеть крошечными.
Чтобы решить эту проблему, я придумал следующий код. Обоснование таково: для всех функций сумма квадратных загрузок всегда равна 1 на ПК. С небольшой долей признаков мы должны привести их так, чтобы сумма их квадратичных загрузок также была равна 1. Этот метод проверен и работает, и он генерирует хорошие графики.
arrows /= np.sqrt((arrows ** 2).sum(axis=0))
Затем мы масштабируем стрелки, чтобы они соответствовали образцам (как обсуждалось выше):
arrows *= np.abs(scores).max(axis=0)
Теперь мы можем визуализировать побочный сюжет:
plt.figure(figsize=(5, 5))
for i, name in enumerate(targets):
plt.scatter(*zip(*scores[y == i]), label=name, s=8, alpha=0.5)
plt.legend(title='Class')
width = -0.005 * np.min([np.subtract(*plt.xlim()), np.subtract(*plt.ylim())])
for i, arrow in zip(tops, arrows):
plt.arrow(0, 0, *arrow, color='k', alpha=0.75, width=width, ec='none',
length_includes_head=True)
plt.text(*(arrow * 1.15), features[i], ha='center', va='center')
for i, axis in enumerate('xy'):
getattr(plt, f'{axis}ticks')([])
getattr(plt, f'{axis}label')(f'PC{i + 1} ({pvars[i]:.2f}%)')
Надеюсь мой ответ будет полезен сообществу.
Я нашел ответ здесь: @teddyroland: https://github.com/teddyroland/python-biplot/blob/master/biplot.py
Чтобы построить загрузку PCA и метки загрузки на двойном графике с помощью matplotlib и scikit-learn, вы можете выполнить следующие шаги:
После подгонки модели PCA с помощью decomposition.PCA извлеките матрицу нагрузок с помощью атрибута component_ модели. Матрица нагрузок представляет собой матрицу нагрузок каждого исходного элемента на каждый главный компонент.
Определите длину матрицы нагрузок и создайте список галочек, используя имена исходных функций.
Нормируйте матрицу нагрузок так, чтобы длина каждого вектора нагрузки равнялась 1. Это облегчит визуализацию нагрузок на побочной диаграмме.
Постройте нагрузки в виде стрелок на побочном графике, используя pyplot.quiver. Установите длину стрелок на абсолютное значение нагрузки и угол на угол нагрузки в комплексной плоскости.
Добавьте метки галочек на побочный график, используяpyplot.xticksиpyplot.yticks.
Вот пример того, как вы можете изменить свой код, чтобы отобразить загрузку PCA и метки загрузки в побочной диаграмме. Добавьте метки загрузки к побочной диаграмме, используяpyplot.text. Вы можете указать положение метки, используя координаты соответствующего вектора нагрузки, и задать размер и цвет шрифта, используя параметры размера и цвета шрифта.
Постройте точки данных на побочном графике, используяpyplot.scatter.
Добавьте легенду к графику, используяpyplot.legendразличать разные виды.
Вот полный код с указанными выше изменениями:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn import decomposition
import seaborn as sns; sns.set_style("whitegrid", {'axes.grid' : False})
%matplotlib inline
np.random.seed(0)
# Iris dataset
DF_data = pd.DataFrame(load_iris().data,
index = ["iris_%d" % i for i in range(load_iris().data.shape[0])],
columns = load_iris().feature_names)
Se_targets = pd.Series(load_iris().target,
index = ["iris_%d" % i for i in range(load_iris().data.shape[0])],
name = "Species")
# Scaling mean = 0, var = 1
DF_standard = pd.DataFrame(StandardScaler().fit_transform(DF_data),
index = DF_data.index,
columns = DF_data.columns)
# Sklearn for Principal Componenet Analysis
# Dims
m = DF_standard.shape[1]
K = 2
# PCA (How I tend to set it up)
Mod_PCA = decomposition.PCA(n_components=m)
DF_PCA = pd.DataFrame(Mod_PCA.fit_transform(DF_standard),
columns=["PC%d" % k for k in range(1,m + 1)]).iloc[:,:K]
# Retrieve the loadings matrix and create the tick labels
loadings = Mod_PCA.components_
tick_labels = DF_data.columns
# Normalize the loadings
loadings = loadings / np.linalg.norm(loadings, axis=1)[:, np.newaxis]
# Plot the loadings as arrows on the biplot
plt.quiver(0, 0, loadings[:,0], loadings[:,1], angles='xy', scale_units='xy', scale=1, color='blue')
# Add the tick labels
plt.xticks(range(-1, 2), tick_labels, rotation='vertical')
plt.yticks(range(-1, 2), tick_labels)
# Add the loading labels
for i, txt in enumerate(tick_labels):
plt.text(loadings[i, 0], loadings[i, 1], txt, fontsize=12, color='blue')
# Plot the data points on the biplot
color_list = [{0:"r",1:"g",2:"b"}[x] for x in Se_targets]
plt.scatter(x=DF_PCA["PC1"], y=DF_PCA["PC2"], color=color_list)