R: Странный pdf квадратичной функции переменной N(0,1): неправильное кодирование или большая ошибка округления?

Question

Я хотел бы рассчитать pdf случайной величины y, определяемой как:

y=c+b*x+a*x^2

PDF является нецентральным распределением хи-квадрат. Для a>0 он должен быть равен нулю, если y меньше d, где d=c-(b^2)/4a.

Как ни странно, при вычислении его с R, PDF-файл стреляет вверх при y> d + e, где e довольно велико.

Есть ли ошибка в моих кодах (ниже) или это ошибка округления? В последнем случае как это решить?

set.seed(101)       
x <- seq(-3.5,3.5,length.out=1000)  
c<-80   
b<-30   
a<-6    
y<-c+b*x+a*(x^2) # g(x) 
## min(y)   

График 1: просто чтобы получить представление о функции

plot(x[order(x)],y[order(x)],   
type="l",lwd=2, xlim=c(-4,4),   
ylab="y",xlab="x",  
main="a. y=g(x)and density of x")   
par(new=T)  
fx<-exp(-0.5*(x^2))/sqrt(2*pi)  
fx<-dnorm(x)    
plot(x[order(x)],fx[order(x)],yaxt="n",xaxt="n",xlab="",ylab="",type="l",lty=2,col="grey")  
axis(4) 
mtext(side=4,"Density",line=2)  
legend("topleft",c("y", "x density"),   
col=c("black","grey"), lty=1:2, lwd=c(1,2), bty="n")    

PDF через метод изменения переменных

g1.c<-(-b+sqrt((b^2)-4*a*(c-y)))/(2*a)  
g2.c<-(-b-sqrt((b^2)-4*a*(c-y)))/(2*a)  
g1.prime.c<-abs(1/sqrt((b^2)-4*a*(c-y)))    
fy<-dnorm(g1.c)*abs(g1.prime.c)+    
dnorm(g2.c)*abs(g1.prime.c) 
min(y)  
d<-c+(-(b^2)/(4*a)) 
plot(y,fy,type="l",lwd=2,ylab="density of y",xlab="y", ylim=c(0,0.015), 
main="y=80+30x+6x^2")   
lines(c(44.4,44.4),c(-1,0.01),lty=2)    
lines(c(d,d),c(-1,max(fy)),lty=2,col="red") 
legend("topright", c("d=42.5","d+e=44.4"),lty=2,col=c("red","black"))   

Видишь, как оно взлетает??

PDF через CDF

d<-c+(-(b^2)/(4*a)) 
first<- 1/(2*sqrt(a)*sqrt(y-d)) 
in_a1<-sqrt(y-d)/sqrt(a)    
in_a2<--sqrt(y-d)/sqrt(a)   
in_b<-b/(2*a)   
A<-in_a1-in_b   
B<-in_a2-in_b   
d   
min(y)  
fy_cdf<-first*(dnorm(A)+dnorm(B))   
plot(y,fy_cdf,type="l",lwd=2,ylab="density of y",xlab="y", ylim=c(0,0.015), 
main="y=80+30x+6x^2")   
lines(c(44.4,44.4),c(-1,0.01),lty=2)    
lines(c(d,d),c(-1,max(fy)),lty=2,col="red") 
legend("topright", c("d=42.5","d+e=44.4"),lty=2,col=c("red","black"))   

Результаты одинаковы, какие бы методы ни использовались для получения PDF

# library("miscTools")  
# compPlot(fy_cdf,fy)   
# diff<-fy_cdf-fy   
# summary(abs(diff)) # these are minor rounding errors, 
# no issue with that.   

Answer 1

Быстрый и грязный эксперимент предполагает, что это реально:

set.seed(101)
x2 <- rnorm(200000)
c <- 80; b<-30; a<-6
y <- c+b*x2+a*(x2^2)
par(las=1)
hist(y,breaks=500,col="gray",border=NA)

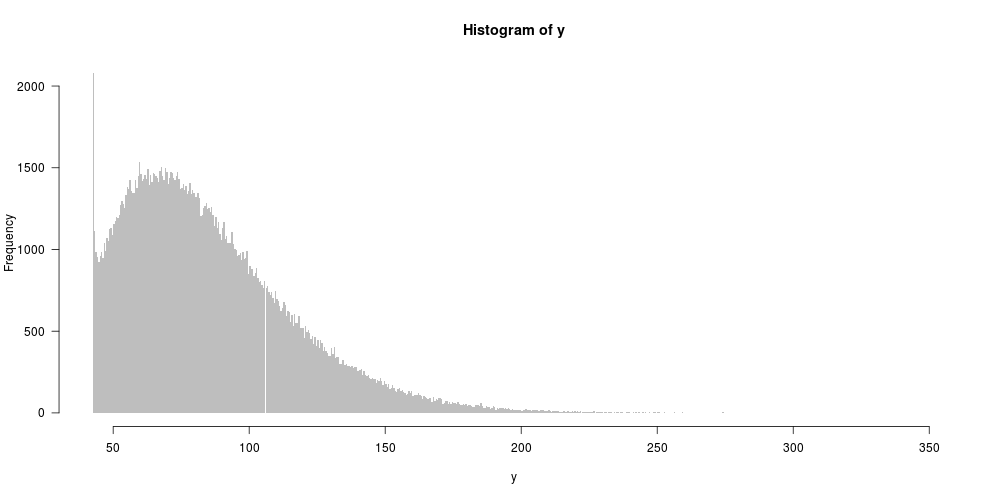
Видите ли вы очень тонкий всплеск или нет, будет немного зависеть от вашего графического разрешения. Увеличьте левый хвост:

hist(y[y<50],breaks=500,col="gray",border=NA)

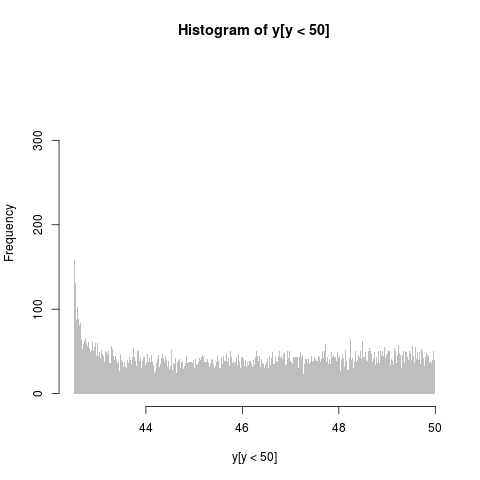
Люди на CrossValidated могут быть заинтересованы в том, чтобы прокомментировать, почему этот PDF расходится по левому краю.