Смешивание двух функций, где одна обратная

Question

Позвольте мне сначала объяснить идею. Актуальный математический вопрос ниже скриншотов. Для музыкальных целей я строю алгоритм канавки, в котором позиции события переводятся математической функцией F(X). Позиции нормализуются внутри диапазона канавок, поэтому я в основном имею дело со значениями от нуля до единицы (что облегчает формирование кривых канавок - единственное ограничение - x'>=0). Этот алгоритм канавки принимает любую позицию события, а также работает, фильтруя статические заметки из структуры данных, такой как дорожка заметки на временной шкале. Для фильтрации событий в определенном диапазоне (размер звукового блока) мне нужна функция обратной канавки, чтобы найти ноты на дорожке и преобразовать их в пространство канавки. Все идет нормально. Оно работает!

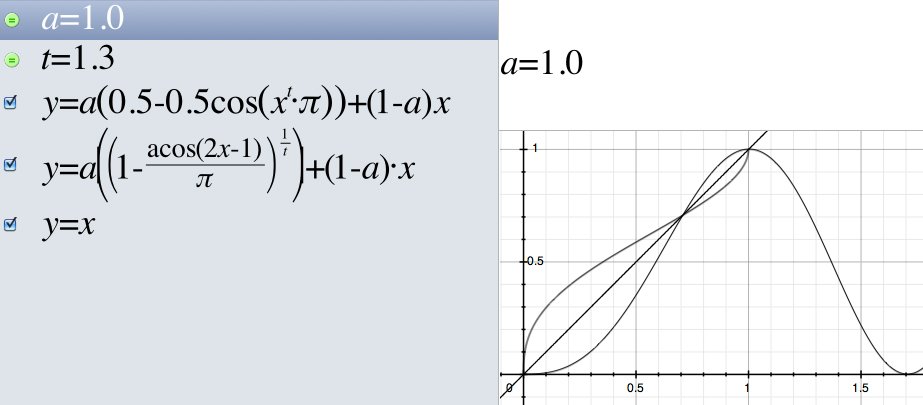
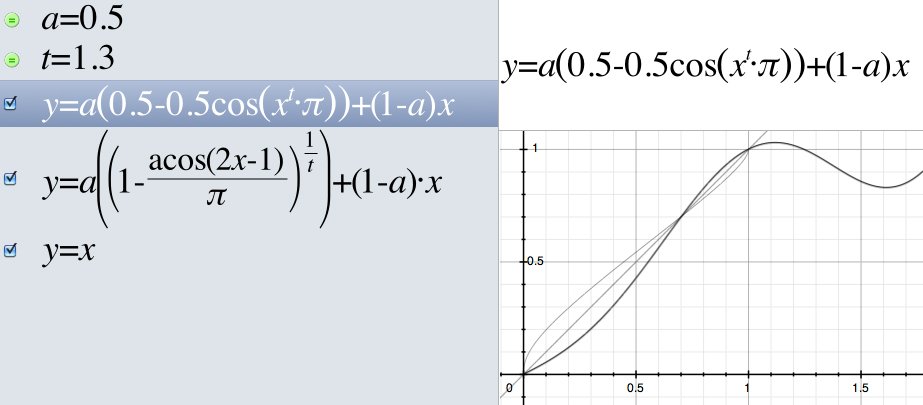
Вкратце: я использую обратную функцию для того факта, что она зеркально отображена в (y=x). Так что я могу подключить значение х и получить у. Этот y, очевидно, может быть подключен к обратной функции, чтобы снова получить первый x.

Проблема: теперь я хочу иметь возможность смешать канавку с другой, но обычный линейный (подсказка подсказки) код смешивания не ведет себя так, как я ожидал. Чтобы было проще, я сначала попытался смешаться с y=x.

B(x)=alpha*F(x) + (1-alpha)*x;
iB(x)=alpha*iF(x) + (1-alpha)*x;

Для альфа =1 мы получаем полную кривую. Для альфа = 0 мы получаем прямую линию. Но для альфа между 0 и 1 B(x) и iB(x) больше не отражаются (близко, но недостаточно), F(x) и iF(x) все еще отражаются.

Есть ли решение для этого (помимо квантования кривой на отрезки)? Любой предмет, на который я должен обратить внимание?

Answer 1

Эта проблема вообще не может быть решена алгебраически.

Рассмотрим для примера

y = 2e^x (обратное x = log 0.5y)

а также

y = 2x (обратное x = 0.5y).

Смешивание их вместе с весом 0,5 дает y = e^x+xи хорошо известно, что невозможно решить x здесь используются только элементарные функции, хотя инверсию каждой части было легко найти.

Вы захотите использовать числовой метод для аппроксимации обратного, как обсуждалось Эндрю выше.

Answer 2

Вы комбинируете две функции, f (x) и g (x), так что y = a f(x) + (1-a) g(x). и учитывая некоторые y, a, f и g, вы хотите найти х. по крайней мере, это то, что я понимаю.

я не понимаю, как это сделать вообще (хотя я не очень старался - я имею в виду, стоило бы спросить кого-то еще), но я подозреваю, что для "хороших" функций, как вы, кажется, используете, Метод Ньютона будет довольно быстрым.

Вы хотите найти x такой, что y = a f(x) + (1-a) g(x). другими словами, когда 0 = a f(x) + (1-a) g(x) - y.

поэтому давайте определим r(x) = a f(x) + (1-a) g(x) - y и найдем "ноль" этого. начните с предположения в середине, x_0 = 0,5. вычислить x_1 = x_0 - r(x_0) / r'(x_0). повторение. если вам повезет, это быстро сойдет (если нет, вы можете подумать об определении функций относительно y=x, что вы, похоже, уже делаете, и попытаться снова).

смотреть википедию