Как узнать, является ли треугольная сетка вогнутой или нет?

Question

Учитывая трехмерную сетку треугольника, как я могу узнать, является ли она выпуклой или вогнутой? Есть ли алгоритм, чтобы проверить это? Если это так, было бы полезно определить диапазон допуска, чтобы игнорировать небольшие вогнутости.

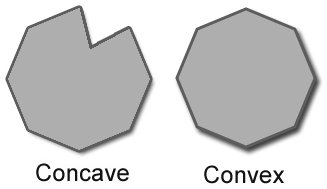
^{Источник изображения: http://www.rustycode.com/tutorials/convex.html}

Answer 1

Выпуклый многогранник можно определить как пересечение конечного числа полупространств. Эти полупространства фактически являются полупространством, определяющим фасеты.

РЕДАКТИРОВАТЬ: Предполагая, что ваша сетка на самом деле определяет многогранник (то есть есть "внутри" и "снаружи")

Вы можете сделать что-то вроде этого (псевдокод):

for each triangle
    p = triangle plane
    n = normal of p (pointing outside)
    d = distance from the origin of p
    //Note: '*' is the dot product.
    //so that X*N + d = 0 is the plane equation
    //if you write a plane equation like (X-P)*n = 0 (where P is any point which lays in the plane), then d = -P*n (it's a scalar).

    for each vertex v in the mesh
         h = v*N + d
         if (h > Tolerance) return NOT CONVEX
         //Notice that when v is a vertex of the triangle from which n and d come from,
         //h is always zero, so the tolerance is required (or you can avoid testing those vertices)
    end
end
return CONVEX

Answer 2

Для простого многоугольника, как вы его описали, вы можете проверить каждый внутренний угол в каждой вершине и проверить, не меньше ли угол 180 градусов. Если это так, то нет никакой вогнутости. Если одна вершина превышает 180°, она вогнутая.

Редактировать: для трехмерных сеток применима та же идея, но вы должны проверять каждую вершину каждого треугольника друг относительно друга, является ли угол между треугольниками выше или ниже 180 °