Как понять проблему с памятью поиска в ширину в ветке и привязке

Question

Как понять проблему с памятью поиска в ширину в ветке и привязке

Недавно меня смутил метод ветвления и привязки. В методе ветвления и привязки есть три стратегии поиска: поиск по глубине, поиск по ширине и поиск по первому. Во всех книгах и литературах утверждается, что в первую очередь и в лучшую очередь потребуется больше памяти для используемого компьютера. Это как понять? Возьмем в качестве примера двоичное дерево, когда для обработки узла (родительского узла) из списка активных узлов генерируются два подузла (или дочерних узла), которые вставляются в список живых узлов, но родительский узел следует удалить. таким образом, увеличивается только память одного узла. С этой точки зрения все три стратегии поиска занимают одинаковые воспоминания о компьютере. Я прав? Это смущало меня долго. Кто-нибудь может дать мне совет?

1

breadth-first-search branch-and-bound

Источник

user3034556 27 фев '17 в 09:53

1 ответ

Другие вопросы по тегам breadth-first-search branch-and-bound

user7193445 01 мар '17 в 09:06 2017-03-01 09:06 · Answer 1 · 2017-03-01 09:06

Что ж,

Вы можете подумать о структурах данных:

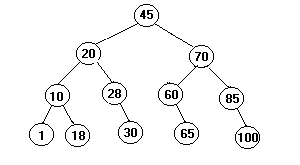
Поиск в ширину : реализован в виде очереди. Когда вы расширяете узел (родительский узел), вы включаете в очередь дочерние узлы. Родительский узел удален. Давайте сделаем пример:

Разверните 45: мы включаем 20 и 70 в очередь и удаляем 45 так:
20 | 70
Разверните 20. Мы расширяем первый узел из очереди и включаем его сыновей:
70 | 10 | 28
Разверните 70: Мы расширяем первый узел из очереди и включаем его сыновей:
10 | 28 | 60 | 85
И так далее...

Как видите, сложность пространства экспоненциальна: O ( 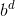) (b = коэффициент ветвления; d = глубина, изначально 0)

Deepth-first-search: реализован как стек:

Разверните 45: мы включаем 20 и 70 в стек и удаляем 45 так:
20 | 70
Разверните 20: Мы расширяем первый узел с вершины стека и включаем его сыновей:
10 | 28 | 70
Разверните 10. Мы расширяем первый узел с вершины стека и включаем его сыновей:
1 | 18 | 28 | 70
И так далее...

Теперь сложность пространства линейна: O (d). Временная сложность составляет О ( 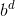) в обоих алгоритмах.

Поиск наилучшего первого: сортирует очередь в соответствии с эвристической функцией оценки f(n) и расширяет преемника с лучшим f(n). Пространственная сложность линейна: O (d).

Надеюсь это поможет.