Найти, находится ли точка внутри выпуклой оболочки для набора точек, не вычисляя саму оболочку

Question

Какой самый простой способ проверить, находится ли точка P внутри выпуклой оболочки, образованной набором точек X?

Я хотел бы алгоритм, который работает в многомерном пространстве (скажем, до 40 измерений), который явно не вычисляет сам выпуклый корпус. Есть идеи?

Answer 1

Проблема может быть решена путем нахождения допустимой точки линейной программы. Если вам интересны полные детали, а не просто вставить LP в существующий решатель, я бы рекомендовал прочитать главу 11.4 в превосходной книге Бойда и Ванденберге по выпуклой оптимизации.

Задавать A = (X[1] X[2] ... X[n])первый столбец v1, второй v2, так далее.

Решить следующую проблему LP,

minimize (over x): 1
s.t.     Ax = P
         x^T * [1] = 1
         x[i] >= 0  \forall i

где

1. x^T это транспонирование x
2. [1] это все-1 вектор.

Задача имеет решение, если точка находится в выпуклой оболочке.

Answer 2

Точка лежит вне выпуклой оболочки других точек тогда и только тогда, когда направление всех векторов от нее к этим другим точкам находится менее чем на половине окружности / сферы / гиперсферы вокруг нее.

Вот эскиз для ситуации с двумя точками: синий внутри выпуклой оболочки (зеленый) и красный снаружи:

Для красного существуют бисекции круга, так что векторы от точки к точкам на выпуклой оболочке пересекают только одну половину круга. Для синей точки не возможно найти такое деление пополам.

Answer 3

Вам не нужно вычислять саму выпуклую оболочку, так как это кажется довольно проблематичным в многомерных пространствах. Есть известное свойство выпуклых оболочек:

Любой вектор (точка) v внутри выпуклой оболочки точек [v1, v2, .., vn] может быть представлен как sum(ki*vi), где 0 <= ki <= 1 а также sum(ki) = 1, Соответственно, ни одна точка вне выпуклой оболочки не будет иметь такого представления.

В м-мерном пространстве это даст нам множество m линейные уравнения с n Неизвестные.

редактировать
Я не уверен в сложности этой новой проблемы в общем случае, но для m = 2 кажется линейным Возможно, кто-то с большим опытом в этой области поправит меня.

Answer 4

У меня была такая же проблема с 16 размерами. Поскольку даже qhull не работал должным образом, так как пришлось генерировать слишком много граней, я разработал свой собственный подход, проверив, можно ли найти разделяющую гиперплоскость между новой точкой и опорными данными (я называю это "HyperHull";)),

Задача нахождения разделяющей гиперплоскости может быть преобразована в задачу выпуклого квадратичного программирования (см.: SVM). Я сделал это в Python, используя cvxopt с менее чем 170 строками кода (включая ввод / вывод). Алгоритм работает без изменений в любом измерении, даже если существует проблема, заключающаяся в том, что чем выше размер, тем выше число точек на корпусе (см.: О выпуклой оболочке случайных точек в многограннике). Поскольку корпус не построен явно, а только проверяется, находится ли точка внутри или нет, алгоритм имеет очень большие преимущества в более высоких измерениях по сравнению, например, с быстрым корпусом.

Этот алгоритм "естественно" можно распараллелить, а ускорение должно быть равно числу процессоров.

Answer 5

Хотя оригинальный пост был три года назад, возможно, этот ответ все равно будет полезен. Алгоритм Гилберта-Джонсона-Керти (GJK) находит кратчайшее расстояние между двумя выпуклыми многогранниками, каждый из которых определяется как выпуклая оболочка набора генераторов - в частности, сам выпуклый корпус вычислять не нужно. В особом случае, о котором идет речь, один из многогранников - это просто точка. Почему бы не попробовать использовать алгоритм GJK для вычисления расстояния между P и выпуклой оболочкой точек X? Если это расстояние равно 0, то P находится внутри X (или, по крайней мере, на его границе). Реализация GJK в Octave/Matlab, называемая ClosestPointInConvexPolytopeGJK.m, вместе с вспомогательным кодом доступна по адресу http://www.99main.com/~centore/MunsellAndKubelkaMunkToolbox/MunsellAndKubelkaMunkToolbox.html. Простое описание алгоритма GJK доступно в разд. 2 статьи, по адресу http://www.99main.com/~centore/ColourSciencePapers/GJKinConstrainedLeastSquares.pdf. Я использовал алгоритм GJK для некоторых очень маленьких наборов X в 31-мерном пространстве и получил хорошие результаты. Сравнение производительности GJK с методами линейного программирования, которые рекомендуют другие, неизвестно (хотя любые сравнения были бы интересны). Метод GJK не позволяет вычислять выпуклую оболочку или выражать оболочку в терминах линейных неравенств, которые могут занимать много времени. Надеюсь, этот ответ поможет.

Answer 6

Готовы ли вы принять эвристический ответ, который обычно должен работать, но не гарантируется? Если да, то вы можете попробовать эту случайную идею.

Пусть f(x) будет кубом расстояния до P, умноженного на число вещей в X, минус сумма кубов расстояния до всех точек в X. Начните где-нибудь случайным образом и используйте алгоритм восхождения на холм, чтобы максимизировать f(x) для x в сфере, которая очень далека от P. За исключением вырожденных случаев, если P не находится в выпуклой оболочке, это должно иметь очень высокую вероятность нахождения нормали к гиперплоскости, P находится на одной стороне от и все в X находится на другой стороне.

Answer 7

Документ для проверки, находится ли точка в пространстве корпуса, с использованием scipy.optimize.minimize.

Основано на ответе пользователя 1071136.

Если вы вычислите выпуклую оболочку, она пойдет намного быстрее, поэтому я добавил пару строк для людей, которые хотят это сделать. Я переключился с сканирования Грэма (только 2D) на алгоритм scipy qhull.

документация scipy.optimize.minimize:
https://docs.scipy.org/doc/scipy/reference/optimize.nonlin.html

import numpy as np
import scipy.optimize
import matplotlib.pyplot as plt
from scipy.spatial import ConvexHull


def hull_test(P, X, use_hull=True, verbose=True, hull_tolerance=1e-5, return_hull=True):
    if use_hull:
        hull = ConvexHull(X)
        X = X[hull.vertices]

    n_points = len(X)

    def F(x, X, P):
        return np.linalg.norm( np.dot( x.T, X ) - P )

    bnds = [[0, None]]*n_points # coefficients for each point must be > 0
    cons = ( {'type': 'eq', 'fun': lambda x: np.sum(x)-1} ) # Sum of coefficients must equal 1
    x0 = np.ones((n_points,1))/n_points # starting coefficients

    result = scipy.optimize.minimize(F, x0, args=(X, P), bounds=bnds, constraints=cons)

    if result.fun < hull_tolerance:
        hull_result = True
    else:
        hull_result = False

    if verbose:
        print( '# boundary points:', n_points)
        print( 'x.T * X - P:', F(result.x,X,P) )
        if hull_result: 
            print( 'Point P is in the hull space of X')
        else: 
            print( 'Point P is NOT in the hull space of X')

    if return_hull:
        return hull_result, X
    else:
        return hull_result

Проверьте на некоторых образцах данных:

n_dim = 3
n_points = 20
np.random.seed(0)

P = np.random.random(size=(1,n_dim))
X = np.random.random(size=(n_points,n_dim))

_, X_hull = hull_test(P, X, use_hull=True, hull_tolerance=1e-5, return_hull=True)

Выход:

# boundary points: 14
x.T * X - P: 2.13984259782e-06
Point P is in the hull space of X

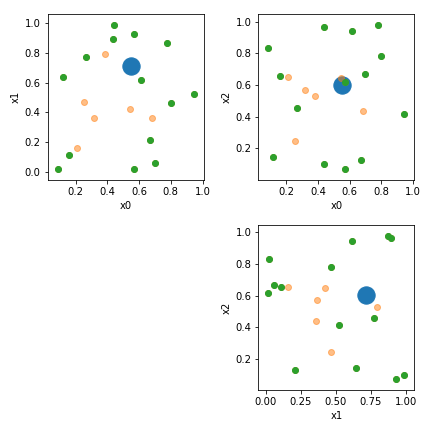
Визуализируйте это:

rows = max(1,n_dim-1)
cols = rows
plt.figure(figsize=(rows*3,cols*3))
for row in range(rows):
    for col in range(row, cols):
        col += 1
        plt.subplot(cols,rows,row*rows+col)
        plt.scatter(P[:,row],P[:,col],label='P',s=300)
        plt.scatter(X[:,row],X[:,col],label='X',alpha=0.5)
        plt.scatter(X_hull[:,row],X_hull[:,col],label='X_hull')
        plt.xlabel('x{}'.format(row))
        plt.ylabel('x{}'.format(col))
plt.tight_layout()