Java: случайное целое число с неравномерным распределением
Как я могу создать случайное целое число n на Яве, между 1 а также k с "линейным нисходящим распределением", т.е. 1 скорее всего, 2 менее вероятно, 3 менее вероятно,..., k наименее вероятно, а вероятности снижаются линейно, например так:
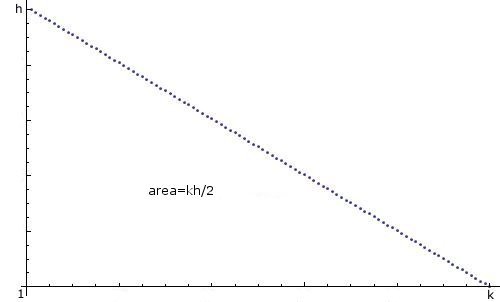
Я знаю, что по этой теме уже есть десятки тем, и я извиняюсь за создание новой, но я не могу создать из них то, что мне нужно. Я знаю что используя import java.util.*;, код
Random r=new Random();
int n=r.nextInt(k)+1;
создает случайное целое число между 1 а также k, распределены равномерно.
ОБОБЩЕНИЕ: любые подсказки для создания произвольно распределенного целого числа, т.е. f(n)=some function, P(n)=f(n)/(f(1)+...+f(k))), также будет оценено, например: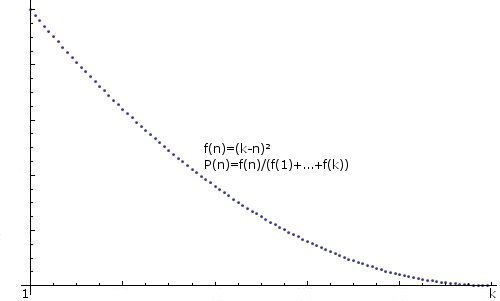 ,
,
10 ответов
Это должно дать вам то, что вам нужно:
public static int getLinnearRandomNumber(int maxSize){
//Get a linearly multiplied random number
int randomMultiplier = maxSize * (maxSize + 1) / 2;
Random r=new Random();
int randomInt = r.nextInt(randomMultiplier);
//Linearly iterate through the possible values to find the correct one
int linearRandomNumber = 0;
for(int i=maxSize; randomInt >= 0; i--){
randomInt -= i;
linearRandomNumber++;
}
return linearRandomNumber;
}
Кроме того, вот общее решение для ПОЗИТИВНЫХ функций (отрицательные функции на самом деле не имеют смысла) в диапазоне от начального индекса до stopIndex:
public static int getYourPositiveFunctionRandomNumber(int startIndex, int stopIndex) {
//Generate a random number whose value ranges from 0.0 to the sum of the values of yourFunction for all the possible integer return values from startIndex to stopIndex.
double randomMultiplier = 0;
for (int i = startIndex; i <= stopIndex; i++) {
randomMultiplier += yourFunction(i);//yourFunction(startIndex) + yourFunction(startIndex + 1) + .. yourFunction(stopIndex -1) + yourFunction(stopIndex)
}
Random r = new Random();
double randomDouble = r.nextDouble() * randomMultiplier;
//For each possible integer return value, subtract yourFunction value for that possible return value till you get below 0. Once you get below 0, return the current value.
int yourFunctionRandomNumber = startIndex;
randomDouble = randomDouble - yourFunction(yourFunctionRandomNumber);
while (randomDouble >= 0) {
yourFunctionRandomNumber++;
randomDouble = randomDouble - yourFunction(yourFunctionRandomNumber);
}
return yourFunctionRandomNumber;
}
Примечание. Для функций, которые могут возвращать отрицательные значения, одним из методов может быть получение абсолютного значения этой функции и его применение к вышеуказанному решению для каждого вызова yourFunction.
Поэтому нам нужно следующее распределение, от наименее вероятного до наиболее вероятного:
*
**
***
****
*****
и т.п.
Давайте попробуем сопоставить равномерно распределенную целочисленную случайную переменную с этим распределением:
1
2 3
4 5 6
7 8 9 10
11 12 13 14 15
и т.п.
Таким образом, если мы генерируем равномерно распределенное случайное целое число от 1 до, скажем, 15 в этом случае для K = 5Нам просто нужно выяснить, какое ведро ему подходит. Самое сложное в том, как это сделать.
Обратите внимание, что числа справа являются треугольными числами! Это означает, что для случайно сгенерированного X от 1 в T_nнам просто нужно найти N такой, что T_(n-1) < X <= T_n, К счастью, существует четко определенная формула для нахождения "треугольного корня" данного числа, которую мы можем использовать в качестве основы нашего отображения от равномерного распределения к сегменту:
// Assume k is given, via parameter or otherwise
int k;
// Assume also that r has already been initialized as a valid Random instance
Random r = new Random();
// First, generate a number from 1 to T_k
int triangularK = k * (k + 1) / 2;
int x = r.nextInt(triangularK) + 1;
// Next, figure out which bucket x fits into, bounded by
// triangular numbers by taking the triangular root
// We're dealing strictly with positive integers, so we can
// safely ignore the - part of the +/- in the triangular root equation
double triangularRoot = (Math.sqrt(8 * x + 1) - 1) / 2;
int bucket = (int) Math.ceil(triangularRoot);
// Buckets start at 1 as the least likely; we want k to be the least likely
int n = k - bucket + 1;
n теперь должен иметь указанное распределение.
Позвольте мне попробовать другой ответ, вдохновленный Rlibby. Это конкретное распределение также является распределением меньшего из двух значений, выбранных равномерно и случайным образом из одного и того же диапазона.
Есть много способов сделать это, но, вероятно, самый простой - просто сгенерироватьдва случайных целых числа, одно между 0 а также k, назови это x, один между 0 а также h, назови это y, Если y > mx + b (m а также b выбрал соответственно...) тогда
k-xиначе x,
Изменить: отвечая на комментарии здесь, чтобы у меня было немного больше места.
В основном мое решение использует симметрию в вашем исходном дистрибутиве, где p(x) является линейной функцией x, Я ответил перед вашим редактированием об обобщении, и это решение не работает в общем случае (потому что в общем случае такой симметрии нет).
Я представлял проблему следующим образом:
- У вас есть два правильных треугольника, каждый
k x hс общей гипотенузой. Композитная форма представляет собойk x hпрямоугольник. - Создайте случайную точку, которая с равной вероятностью падает на каждую точку прямоугольника.
- Половина времени это попадет в один треугольник, половина в другой.
- Предположим, точка падает в нижнем треугольнике.
- Треугольник в основном описывает PMF, а "высота" треугольника над каждым значением x описывает вероятность того, что точка будет иметь такое значение x. (Помните, что мы имеем дело только с точками в нижнем треугольнике.) Таким образом, получим значение x.
- Предположим, точка попадает в верхний треугольник.
- Инвертируйте координаты и обработайте их, как указано выше, с нижним треугольником.
Вам также придется позаботиться о крайних случаях (я не беспокоился). Например, теперь я вижу, что ваш дистрибутив начинается с 1, а не с 0, так что там есть одно за другим, но это легко исправить.
Нет необходимости моделировать это с массивами и тому подобным, если ваше распределение таково, что вы можете вычислить его интегральную функцию распределения (cdf). Выше у вас есть функция распределения вероятности (pdf). h на самом деле определяется, так как площадь под кривой должна быть 1. Для простоты математики позвольте мне также предположить, что вы выбираете число в [0,k).
PDF здесь f(x) = (2/k) * (1 - x/k), если я правильно вас понял. Cdf просто является неотъемлемой частью PDF. Здесь это F(x) = (2/k) * (x - x^2 / 2k). (Вы можете повторить эту логику для любой функции PDF, если она интегрируема.)
Затем вам нужно вычислить обратную функцию cdf, F^-1(x), и если бы я не был ленивым, я бы сделал это для вас.
Но хорошая новость заключается в следующем: когда у вас есть F ^ -1 (x), все, что вы делаете, это применяете его к распределению случайных значений равномерно в [0,1] и применяете к нему функцию. Случайный может предоставить это с некоторой осторожностью. Это ваше случайно выбранное значение из вашего дистрибутива.
Это называется треугольным распределением, хотя у вас вырожденный случай с модой, равной минимальному значению. В Википедии есть уравнения для того, как создать одну заданную равномерно распределенную (0,1) переменную.
Кумулятивная функция распределения x^2 для треугольного распределения [0,1] с режимом (наибольшая взвешенная вероятность) 1, как показано здесь.
Поэтому все, что нам нужно сделать, чтобы преобразовать единообразное распределение (например, Java Random::nextDouble) в удобное треугольное распределение, взвешенное в направлении 1: просто взять квадратный корень Math.sqrt(rand.nextDouble()), который затем можно умножить на любой желаемый диапазон.
Для вашего примера:
int a = 1; // lower bound, inclusive
int b = k; // upper bound, exclusive
double weightedRand = Math.sqrt(rand.nextDouble()); // use triangular distribution
weightedRand = 1.0 - weightedRand; // invert the distribution (greater density at bottom)
int result = (int) Math.floor((b-a) * weightedRand);
result += a; // offset by lower bound
if(result >= b) result = a; // handle the edge case
Что-то вроде этого....
class DiscreteDistribution
{
// cumulative distribution
final private double[] cdf;
final private int k;
public DiscreteDistribution(Function<Integer, Double> pdf, int k)
{
this.k = k;
this.cdf = new double[k];
double S = 0;
for (int i = 0; i < k; ++i)
{
double p = pdf.apply(i+1);
S += p;
this.cdf[i] = S;
}
for (int i = 0; i < k; ++i)
{
this.cdf[i] /= S;
}
}
/**
* transform a cumulative distribution between 0 (inclusive) and 1 (exclusive)
* to an integer between 1 and k.
*/
public int transform(double q)
{
// exercise for the reader:
// binary search on cdf for the lowest index i where q < cdf[i]
// return this number + 1 (to get into a 1-based index.
// If q >= 1, return k.
}
}
Первое решение, которое приходит на ум, - это использование заблокированного массива. Каждый индекс будет указывать диапазон значений в зависимости от того, насколько "вероятным" он будет. В этом случае вы будете использовать более широкий диапазон для 1, менее широкий для 2 и так далее, пока не достигнете небольшого значения (скажем, 1) для k.
int [] indexBound = new int[k];
int prevBound =0;
for(int i=0;i<k;i++){
indexBound[i] = prevBound+prob(i);
prevBound=indexBound[i];
}
int r = new Random().nextInt(prevBound);
for(int i=0;i<k;i++){
if(r > indexBound[i];
return i;
}
Теперь проблема в том, чтобы просто найти случайное число, а затем сопоставить это число с его корзиной. Вы можете сделать это для любого распределения при условии, что вы можете дискретизировать ширину каждого интервала. Дайте мне знать, если я что-то упускаю, объясняя алгоритм или его правильность. Излишне говорить, что это должно быть оптимизировано.
Проще всего сделать это, чтобы сгенерировать список или массив всех возможных значений в их весах.
int k = /* possible values */
int[] results = new int[k*(k+1)/2];
for(int i=1,r=0;i<=k;i++)
for(int j=0;j<=k-i;j++)
results[r++] = i;
// k=4 => { 1,1,1,1,2,2,2,3,3,4 }
// to get a value with a given distribution.
int n = results[random.nextInt(results.length)];
Это лучше всего работает при относительно небольших значениях k. к < 1000.;)
Для больших чисел вы можете использовать ведро подход
int k =
int[] buckets = new int[k+1];
for(int i=1;i<k;i++)
buckets[i] = buckets[i-1] + k - i + 1;
int r = random.nextInt(buckets[buckets.length-1]);
int n = Arrays.binarySearch(buckets, r);
n = n < 0 ? -n : n + 1;
Стоимость бинарного поиска довольно мала, но не так эффективна, как прямой поиск (для небольшого массива)
Для произвольного распределения вы можете использовать double[] для накопительного распределения и используйте бинарный поиск, чтобы найти значение.
Есть много способов сгенерировать случайное целое число с настраиваемым распределением (также известным как дискретное распределение). Выбор зависит от многих вещей, в том числе от количества целых чисел на выбор, формы распределения и от того, изменится ли распределение со временем.
Один из самых простых способов выбрать целое число с помощью специальной весовой функции f(x)- метод отбраковочной выборки. Ниже предполагается, что максимально возможное значениеf является max. Временная сложность выборки отбраковки в среднем постоянна, но сильно зависит от формы распределения и в худшем случае работает вечно. Чтобы выбрать целое число в [1,k] с использованием отбраковочной выборки:
- Выберите равномерное случайное целое число
iв 1,k]. - С вероятностью
f(i)/max, возвращениеi. В противном случае переходите к шагу 1.
Другие алгоритмы имеют среднее время выборки, которое не так сильно зависит от распределения (обычно либо постоянное, либо логарифмическое), но часто требует, чтобы вы предварительно вычислили веса на этапе настройки и сохранили их в структуре данных. Некоторые из них также экономичны с точки зрения количества используемых в среднем случайных битов. Эти алгоритмы включают в себя метод псевдонима, Fast Loaded Dice Roller, алгоритм Кнута – Яо, структуру данных MVN и многое другое. См. Мой раздел " Замечание об алгоритмах взвешенного выбора" для обзора.