Что если я хочу одну модель линейной регрессии, а не "млм"?
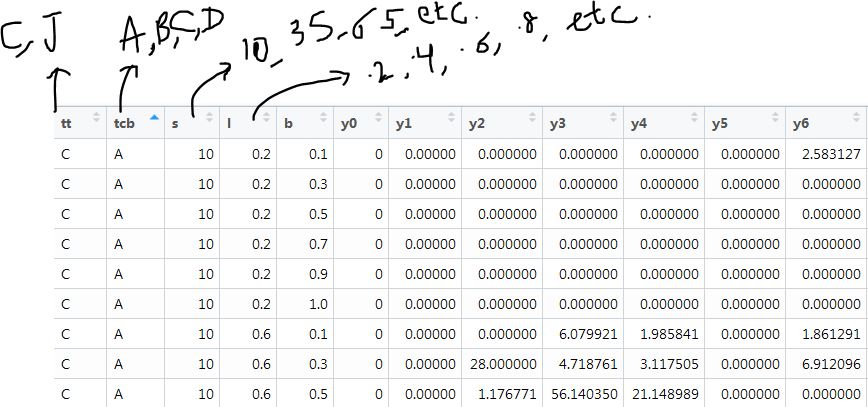
Я поделился первыми 9 строками данных, над которыми я работаю, на изображении ниже (y0 в y6 выходы, остальные входы):
Моя цель - получить подходящие выходные данные для y0 в y6,
Я старался lm Функция в R с помощью команд:
lm1 <- lm(cbind(y0, y1, y2, y3, y4, y5, y6) ~ tt + tcb + s + l + b, data = table3)
summary(lm1)
И он вернул 7 наборов коэффициентов типа "Ответ y0", "Отклик y1", так далее.
То, что я действительно хочу, это просто 1 набор коэффициентов, которые могут предсказать значения для выходных y0 в y6,
Не могли бы вы помочь в этом?
1 ответ
От cbind(y0, y1, y2, y3, y4, y5, y6) мы соответствуем 7 независимым моделям (что будет лучшей идеей).
Для того, что вы ищете, сложите y* переменные, реплицировать другие независимые переменные и сделать одну регрессию.
Y <- c(y0, y1, y2, y3, y4, y5, y6)
tt. <- rep(tt, times = 7)
tcb. <- rep(tcb, times = 7)
s. <- rep(s, times = 7)
l. <- rep(l, times = 7)
b. <- rep(b, times = 7)
fit <- lm(Y ~ tt. + tcb. + s. + l. + b.)
Прогнозируемые значения для y* являются
matrix(fitted(fit), ncol = 7)
Для других читателей, чем OP
Настоящим я готовлю крошечный воспроизводимый пример (только с одним ковариатом x и две копии y1, y2), чтобы помочь вам переварить проблему.
set.seed(0)
dat_wide <- data.frame(x = round(runif(4), 2),
y1 = round(runif(4), 2),
y2 = round(runif(4), 2))
# x y1 y2
#1 0.90 0.91 0.66
#2 0.27 0.20 0.63
#3 0.37 0.90 0.06
#4 0.57 0.94 0.21
## The original "mlm"
fit_mlm <- lm(cbind(y1, y2) ~ x, data = dat_wide)
Вместо того чтобы делать c(y1, y2) а также rep(x, times = 2)Я бы использовал reshape функция из базового пакета R stats, поскольку такая операция, по сути, представляет собой преобразование набора данных из широких в длинные.
dat_long <- stats::reshape(dat_wide, ## wide dataset
varying = 2:3, ## columns 2:3 are replicates
v.names = "y", ## the stacked variable is called "y"
direction = "long" ## reshape to "long" format
)
# x time y id
#1.1 0.90 1 0.91 1
#2.1 0.27 1 0.20 2
#3.1 0.37 1 0.90 3
#4.1 0.57 1 0.94 4
#1.2 0.90 2 0.66 1
#2.2 0.27 2 0.63 2
#3.2 0.37 2 0.06 3
#4.2 0.57 2 0.21 4
Дополнительные переменные time а также id созданы. Первый рассказывает, из какой копии происходит дело; последний говорит, какая запись этого случая находится в пределах копии.
Чтобы соответствовать одной модели для всех копий, мы делаем
fit1 <- lm(y ~ x, data = dat_long)
#(Intercept) x
# 0.2578 0.5801
matrix(fitted(fit1), ncol = 2) ## there are two replicates
# [,1] [,2]
#[1,] 0.7798257 0.7798257
#[2,] 0.4143822 0.4143822
#[3,] 0.4723891 0.4723891
#[4,] 0.5884029 0.5884029
Не удивляйтесь, что две колонки идентичны; в конце концов, существует только один набор коэффициентов регрессии для обоих повторов.
Если вы внимательно подумаете, мы можем сделать следующее:
dat_wide$ymean <- rowMeans(dat_wide[2:3]) ## average all replicates
fit2 <- lm(ymean ~ x, data = dat_wide)
#(Intercept) x
# 0.2578 0.5801
и мы получим одинаковые точечные оценки. Стандартные ошибки и другие сводные статистические данные будут отличаться, поскольку две модели имеют разный размер выборки.
coef(summary(fit1))
# Estimate Std. Error t value Pr(>|t|)
#(Intercept) 0.2577636 0.2998382 0.8596755 0.4229808
#x 0.5800691 0.5171354 1.1216967 0.3048657
coef(summary(fit2))
# Estimate Std. Error t value Pr(>|t|)
#(Intercept) 0.2577636 0.01385864 18.59949 0.002878193
#x 0.5800691 0.02390220 24.26844 0.001693604