PortfolioAnalytics - ROI optimize.rebalancing с использованием деноминированных ежемесячных цен дает неверный результат?
Надеюсь, что кто-то может помочь или испытал подобную ситуацию, чтобы указать мне на то, что идет не так.
Вот мои настройки (см., Возможно, воспроизводимый код ниже):
- построить список символов
- получить данные инструмента через FinancialInstrument от Yahoo
- получить обменный курс EURUSD от Quandl - требуется токен авторизации
- переименовать цены в базовую валюту портфеля
- построить ежемесячные доходы с 2004-03-31 до сегодняшнего дня для активов в их валюте и по деноминированным ценам (здесь EUR)
- провести оптимизацию ROI с ребалансировкой
Проблема:
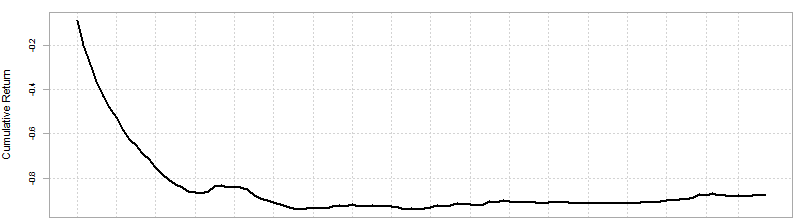
Использование доходности от деноминированных цен, по-видимому, приводит к неверным результатам оптимизации при перебалансировке по месяцам (см. Рисунок), поскольку доходность не гарантирует такой кривой доходности, поскольку большая часть портфеля инвестируется в "TLT" - казначейские обязательства на 20 лет.
Это дает результат оптимизации, как показано на следующем рисунке:
Это часть большей системы, но я надеюсь, что я создал воспроизводимый код, который показывает проблему, которая, кажется, применима только при использовании перебалансировки, что указывало мне на то, что может быть проблема с index или даты. Однако при экспорте обоих возвратов xts в Excel я не увидел никакой разницы.
Я добавил несколько графиков в конец кода, так как мне не разрешено публиковать более двух изображений в данный момент.
Любая помощь или советы очень ценны, чтобы указать мне на то, что происходит...
packages <- c('quantmod', 'FinancialInstrument', 'PortfolioAnalytics', 'Quandl')
for(i in 1:length(packages))
library(packages[i], character.only = TRUE, quietly = TRUE)
.baseOptions <- list()
# set base CCY
.baseOptions$portf$portfolio.base.ccy <- "EUR"
# set date from which the analysis should be started
.baseOptions$portf$analyse.from <- "2004-03-31/"
# set symbols
symbol.list <- c("LQD", #iShares Investment Grade Corporate Bonds
"SHY", #iShares 1-3 year TBonds
"IEF", #iShares 3-7 year TBonds
"TLT" #iShares 20+ year Bonds
)
# get symbols while adjusting to dividends & splits
getSymbols(symbol.list, auto.assign = TRUE, from = "1990-01-01", to = as.character(Sys.Date()), adjust = TRUE)
# set CCY
currency(c("USD", "EUR"))
# set exchange_rate
exchange_rate("EURUSD")
# get exchange_rate
EURUSD <- Quandl('ECB/EURUSD', type = "xts", collapse = "daily", order = "asc")
stock(symbol.list, currency = "USD")
# get Fininstrument Data
update_instruments.yahoo(symbol.list)
#View(instrument.table(ls_instruments()))
# build price xts - usually part of larger sytem with different CCY incl. JPY, GBP, USD, HKD etc.
asset.CCY.prices <- foreach(i=1:length(symbol.list), .combine = 'cbind', .packages=c('quantmod')) %dopar% {
asset.CCY.prices <- Cl(get(symbol.list[i]))
}
# set to analysis period & monthly
asset.CCY.prices <- asset.CCY.prices[endpoints(asset.CCY.prices, on = "months")][.baseOptions$portf$analyse.from]
# redenominate to EUR
base.CCY.prices <- foreach (i=1:length(colnames(asset.CCY.prices)), .combine = 'cbind', .packages=c('FinancialInstrument')) %dopar% {
current.instrument <- gsub(".Close", "", colnames(asset.CCY.prices)[i])
current.instrument.CCY <- getInstrument(gsub(".Close", "", colnames(asset.CCY.prices)[i]))$currency
if(current.instrument.CCY != .baseOptions$portf$portfolio.base.ccy)
base.CCY.prices <- redenominate(asset.CCY.prices[,i],
new_base = .baseOptions$portf$portfolio.base.ccy,
old_base = current.instrument.CCY)
}
rm(current.instrument, current.instrument.CCY, i, packages)
# set the colnames in the basee.CCY price .xts
colnames(base.CCY.prices) <- colnames(asset.CCY.prices) # unlist(lapply(symbol.list, function(x) paste(x, .baseOptions$portf$portfolio.base.ccy, sep = ".")))
# build returns
asset.CCY.R <- ROC(asset.CCY.prices)
base.CCY.R <- ROC(base.CCY.prices)
# portfolio optimization
#
#
#-----------------------------------
# Specify initial portfolio
if(exists("portf.init")) rm(portf.init)
portf.init <- portfolio.spec(assets=colnames(asset.CCY.R))
portf.init <- add.constraint(portfolio=portf.init, type="weight_sum", min_sum=0.99, max_sum=1.01)
portf.init <- add.constraint(portfolio=portf.init, type="long_only")
#portf.init <- add.constraint(portfolio=portf.init, type="position_limit", max_pos=15)
#' Add objective to maximize mean
portf.init <- add.objective(portfolio=portf.init, type="return", name="mean")
#----------------------------------
# Global Minimum Variance Portfolio
#
if(exists("GMV")) rm(GMV)
GMV <- add.constraint(portfolio=portf.init, type="weight_sum", min_sum=0.90, max_sum=1.01, indexnum = 1)
# Add box constraint
GMV <- add.constraint(GMV, type="box", min=0, max=0.99)
# Add var objective - risk is always minimised
GMV <- add.objective(GMV, type = "risk", name = "var")
# optimization in asset.CCY
opt.asset.CCY = optimize.portfolio.rebalancing(R = asset.CCY.R, portfolio = GMV, rebalance_on = "months", optimize_method = "ROI")
port.data.asset.CCY <- Return.portfolio(R = asset.CCY.R, weights = extractWeights(opt.asset.CCY), verbose=TRUE)
#optimization in base.CCY
opt.base.CCY = optimize.portfolio.rebalancing(R = base.CCY.R, portfolio = GMV, rebalance_on = "months", optimize_method = "ROI")
port.data.base.CCY <- Return.portfolio(R = base.CCY.R, weights = extractWeights(opt.base.CCY), verbose=TRUE)
opt.base.CCY.simple = optimize.portfolio(R = base.CCY.R, portfolio = GMV, optimize_method = "ROI")
port.data.base.CCY.simple <- Return.portfolio(R = base.CCY.R, weights = extractWeights(opt.base.CCY.simple), verbose=TRUE)
#--------- START EDIT 04.01.2016 ---------
#
class(index(asset.CCY.R))
indexTZ(asset.CCY.R)
# Indexed by Class Date - XTS though shows TZ = UTC
# this should however not cause any issues
all.equal(index(asset.CCY.R), index(base.CCY.R))
# TRUE
# Weights after rebalancing
class(index(extractWeights(opt.asset.CCY)))
# "POSIXct" "POSIXt" which should be fine as well
all.equal(index(extractWeights(opt.asset.CCY)),
index(extractWeights(opt.base.CCY)))
# TRUE
#
#--------- END EDIT 04.01.2016 ---------
# charts
#
op <- par(mfrow = c(2, 2), pty = "m")
# chart the time series
chart.TimeSeries(asset.CCY.prices, main = 'Timeseries - Asset.CCY', legend.loc = "top")
# chart the performance summaries
chart.CumReturns(asset.CCY.R, main = "Cum Returns - Asset.CCY")
# chart the time series
chart.TimeSeries(base.CCY.prices, main = 'Base.CCY', legend.loc = "top")
# chart the performance summaries
chart.CumReturns(base.CCY.R, main = "Cum Returns - Base.CCY")
# Optimized returns - rebalancing
chart.CumReturns(port.data.asset.CCY$returns, main=paste("Asset.CCY", "Opt Return" , sep= " - "))
chart.CumReturns(port.data.base.CCY$returns, main=paste("Base.CCY", "Opt Return" , sep= " - "))
# Optimized returns - no rebalancing
chart.CumReturns(port.data.base.CCY.simple$returns, main=paste("Base.CCY.simple", "Opt Return" , sep= " - "))
# optimizes EOP Value Charts
chart.StackedBar(port.data.asset.CCY$EOP.Value[ , !apply(port.data.asset.CCY$EOP.Value==0,2,all)], main=paste("Asset.CCY", "Value" , sep= " - "))
chart.StackedBar(port.data.base.CCY$EOP.Value[ , !apply(port.data.base.CCY$EOP.Value==0,2,all)], main=paste("Base.CCY", "Value" , sep= " - "))
# Optimized EOP Value - no rebalancing
chart.StackedBar(port.data.base.CCY.simple$EOP.Value[ , !apply(port.data.base.CCY.simple$EOP.Value==0,2,all)], main=paste("Base.CCY.simple", "Value" , sep= " - "))
# optmized Contribution charts
chart.StackedBar(port.data.asset.CCY$contribution[ , !apply(port.data.asset.CCY$contribution==0,2,all)], main=paste("Asset.CCY", "Contribution" , sep= " - "))
chart.StackedBar(port.data.base.CCY$contribution[ , !apply(port.data.base.CCY$contribution==0,2,all)], main=paste("Base.CCY", "Contribution" , sep= " - "))
# optmized Contribution charts - no rebalancing
chart.StackedBar(port.data.base.CCY.simple$contribution[ , !apply(port.data.base.CCY.simple$contribution==0,2,all)], main=paste("Base.CCY.simple", "Contribution" , sep= " - "))
# restore usual charting
par(op)
sessionInfo()
R version 3.2.2 (2015-08-14)
Platform: x86_64-w64-mingw32/x64 (64-bit)
Running under: Windows 8 x64 (build 9200)
locale:
[1] LC_COLLATE=English_United Kingdom.1252 LC_CTYPE=English_United Kingdom.1252 LC_MONETARY=English_United Kingdom.1252
[4] LC_NUMERIC=C LC_TIME=English_United Kingdom.1252
attached base packages:
[1] parallel stats graphics grDevices utils datasets methods base
other attached packages:
[1] PortfolioAnalytics_1.0.3636 XML_3.98-1.3 FinancialInstrument_1.2.0 RColorBrewer_1.1-2
[5] reshape2_1.4.1 doParallel_1.0.10 iterators_1.0.8 rCharts_0.4.5
[9] RcppDE_0.1.4 timeDate_3012.100 sqldf_0.4-10 RSQLite_1.0.0
[13] DBI_0.3.1 gsubfn_0.6-6 proto_0.3-10 stringr_1.0.0
[17] ggplot2_1.0.1 xlsx_0.5.7 xlsxjars_0.6.1 rJava_0.9-7
[21] quantmod_0.4-5 TTR_0.23-0 Quandl_2.7.0 ProjectTemplate_0.6
[25] PerformanceAnalytics_1.4.3541 foreach_1.4.3 xts_0.9-7 zoo_1.7-12
РЕДАКТИРОВАТЬ 01/01/2016 Просто еще раз рассмотрел этот вопрос, поскольку он остается проблематичным для повторно назначенных тестовых портфелей.
Я предположил, что проблема может быть вызвана некоторыми эффектами часового пояса и добавил несколько проверок (см. Код выше перед диаграммами). Индексы объектов return-xts, а также объектов weight-xts остаются равными (all.equal() возвращает TRUE).
Отладка в функцию return.portfolio(),
- base.CCY.R и asset.CCY.R определены как ежемесячная частота и дата начала 2004-03-30.
- веса обозначены как xts (строка 55) и обеспечивают следующий первый индекс.
Следующие чеки все равны для весов в активе или базовой валюте:
Sys.timezone()
# [1] "Europe/Berlin"
first(index(weights))
# [1] "2007-03-30 CEST"
as.numeric(first(index(weights)))
# [1] 1175205600
class(index(weights))
# [1] "POSIXct" "POSIXt"
as.Date(first(index(weights))
# [1] "2007-03-29"
На странице справки для as.Date это предполагает "UTC" для "POSIXct", и, следовательно, я предполагаю, что разница, однако следующая также возвращает 29-е:
as.Date(first(index(weights), tz = "Europe/Berlin"))
# [1] "2007-03-29"
Это не ясно для меня, но это согласуется как с весом XTS, так и не является частью этого вопроса.
В строке 72 return.portfolio теперь уменьшает возвращаемые xts до того же начального индекса, выполнив:
R <- R[paste0(as.Date(index(weights[1, ])) + 1, "/")]
После этого вызывается метод Return.portfolio.geometric(), который показывает, что веса для оптимизации в деноминированных ценах приводят к весам ниже максимума 1,01.
Что также можно увидеть, выполнив rowSum() для извлеченных весов:
#--------- START EDIT 04.01.2016 ---------
rowSums(extractWeights(opt.asset.CCY))
# [1] 1.01 1.01 1.01 1.01 1.01 1.01 1.01 1.01 1.01 1.01 1.01
# [12] 1.01 1.01 1.01 1.01 1.01 1.01 1.01 1.01 1.01 1.01 1.01
# [23] 1.01 1.01 1.01 1.01 1.01 1.01 1.01 1.01 1.01 1.01 1.01
# [34] 1.01 1.01 1.01 1.01 1.01 1.01 1.01 1.01 1.01 1.01 1.01
# [45] 1.01 1.01 1.01 1.01 1.01 1.01 1.01 1.01 1.01 1.01 1.01
# [56] 1.01 1.01 1.01 1.01 1.01 1.01 1.01 1.01 1.01 1.01 1.01
# [67] 1.01 1.01 1.01 1.01 1.01 1.01 1.01 1.01 1.01 1.01 1.01
# [78] 1.01 1.01 1.01 1.01 1.01 1.01 1.01 1.01 1.01 1.01 1.01
# [89] 1.01 1.01 1.01 1.01 1.01 1.01 1.01 1.01 1.01 1.01 1.01
# [100] 1.01 1.01 1.01 1.01 1.01 1.01 1.01
rowSums(extractWeights(opt.base.CCY))
# [1] 0.9000000 0.9000000 0.9000000 0.9000000 0.9000000
# [6] 0.9000000 0.9000000 0.9000000 0.9000000 0.9000000
# [11] 0.9000000 0.9000000 0.9000000 0.9000000 0.9000000
# [16] 0.9000000 0.9000000 0.9000000 0.9000000 1.0100000
# [21] 1.0100000 1.0100000 1.0100000 1.0100000 1.0100000
# [26] 1.0100000 0.9000000 0.9000000 0.9000000 0.9000000
# [31] 0.9000000 0.9000000 0.9000000 0.9000000 0.9937606
# [36] 1.0100000 1.0100000 1.0100000 1.0100000 1.0100000
# [41] 1.0100000 1.0100000 1.0100000 1.0100000 1.0100000
# [46] 1.0100000 1.0100000 1.0100000 0.9666945 0.9000000
# [51] 1.0100000 1.0100000 1.0100000 1.0100000 1.0100000
# [56] 1.0100000 1.0100000 1.0100000 1.0100000 1.0100000
# [61] 1.0100000 1.0100000 1.0100000 1.0100000 1.0100000
# [66] 1.0100000 1.0100000 1.0100000 1.0100000 1.0100000
# [71] 1.0100000 1.0100000 1.0100000 1.0100000 1.0100000
# [76] 1.0100000 1.0100000 1.0100000 1.0100000 1.0100000
# [81] 1.0100000 1.0100000 1.0100000 1.0100000 1.0100000
# [86] 1.0100000 1.0100000 1.0100000 1.0100000 1.0100000
# [91] 1.0100000 1.0100000 1.0100000 1.0100000 1.0100000
# [96] 1.0100000 1.0100000 1.0100000 1.0100000 1.0100000
# [101] 1.0100000 1.0100000 1.0100000 1.0100000 1.0100000
# [106] 1.0100000
#--------- END EDIT 04.01.2016 ---------
РЕДАКТИРОВАТЬ 01/01/2016
После дальнейшего изучения кода Return.portfolio.geometric() из пакета PerformanceAnaytics, который вызывается Return.portfolio():
- Итерация и расчет возврата
В строке 49:
ret[k] = eop_value_total[k]/end_value - 1
При этом рассчитывается доходность портфеля, и в этом примере он будет равен 0,877/1 - 1, что, очевидно, должно привести к доходности -12,3%.
Если я увижу это право, это будет означать, что весы будут равны 100% как end_value, если пользователь не предоставил их в настройке значения во время вызова Return.portfolio (), установленном в 1 или 100%.
end_value для следующей итерации будет тогда 0,877
end_value = eop_value_total[k]
- Итерация и возврат
и новое начальное значение портфеля для следующего периода 0,877, умноженное на вес следующих периодов снова 90% или 0,90 = 0,7893
bop_value[k, ] = end_value * weights[i, ]
Как и в первой итерации, отрицательный доход будет снова завышен из-за 90% общего веса, рассчитанного пакетом PortfolioAnalytics из-за ограничения weight_sum.
ret[k] = eop_value_total[k]/end_value - 1
Переводит в 0,78/0,877 - 1 = -0,111
Вопросы, которые приходят ко мне тогда:
- Как рассчитать правильную прибыль, если вес <> 100% или 1?
- Имеет ли смысл ограничение веса <100% на самом деле? В реальном сценарии недостающий%, вероятно, будет наличными / краткосрочными облигациями?
- Исходя из этого, варианты могут включать добавление денежных возвратов в оптимизацию при использовании ограничения full_investment или, в качестве альтернативы, нельзя было бы либо настроить функцию геометрического возврата для предупреждения о весах <> 100%, либо включить логику для весов <> 100%?
И последнее, но не менее важное: что-то не так с моими индексами дат?
Не уверен, что кто-то все еще читает это, но опять же, любая поддержка или понимание будет высоко ценится. Большое спасибо!