Matlab: Невозможно выполнить обратную операцию - Как создать неособую квадратную матрицу

Question

Я пытаюсь матричные операции. Данные представляют собой модель временного ряда - модель авторегрессии, AR(2), где порядок модели p =2 представлен переменной Y возбуждается белым гауссовским шумом, epsilon, Я застрял с концептуальными вопросами, на которые я буду благодарен за ответы. Код вычисляет матрицу автокорреляции после умножения вектора выборки с задержкой по времени Y на транспонирование вектора задержки с выдержкой времени в 1 выборку. Общая формула для корреляции E(Y*Y'), В этом случае мне нужно сделать E(Y(1:end)*Y(1:end)'), Ответ скаляр, если сделано так. Но, основываясь на ответе математического ожидания Уолтера Робертса, я могу получить 9 by 9 matrix, Однако я не получаю неособую матрицу.

Как создать особую матрицу для матрицы автокорреляции, чтобы можно было вычислить обратную величину? Пожалуйста помоги

КОД:

clc;
clear all;
 var_eps = 1;
    epsilon = sqrt(var_eps)*randn(5000,1); % Gaussian signal exciting the AR model

   Y(1) = 0.0;
    Y(2) = 0.0;
    for n= 3:5000
    Y(n)=  0.1950*Y(n-1) -0.9500*Y(n-2)+ epsilon(n); %AR(2) model
    end

  y_tminus1 = Y(1:end-1).';
    mult = y_tminus1*y_tminus1';  %This creates a square matrix
    autocorr = xcorr2(mult);  %To perform autocorrelation of 1 sampled lag time series with itself(1 sampled lag)
  inverse_autocorr = inv(autocorr);  **%PROBLEM**        


%Warning: Matrix is singular to working precision. 
  trace_inv=trace(inverse_autocorr);

ОБНОВЛЕНИЕ: я сталкиваюсь с этой проблемой, так как я пытаюсь реализовать условия матрицы в выражении уравнения (20) и RHS уравнения (24)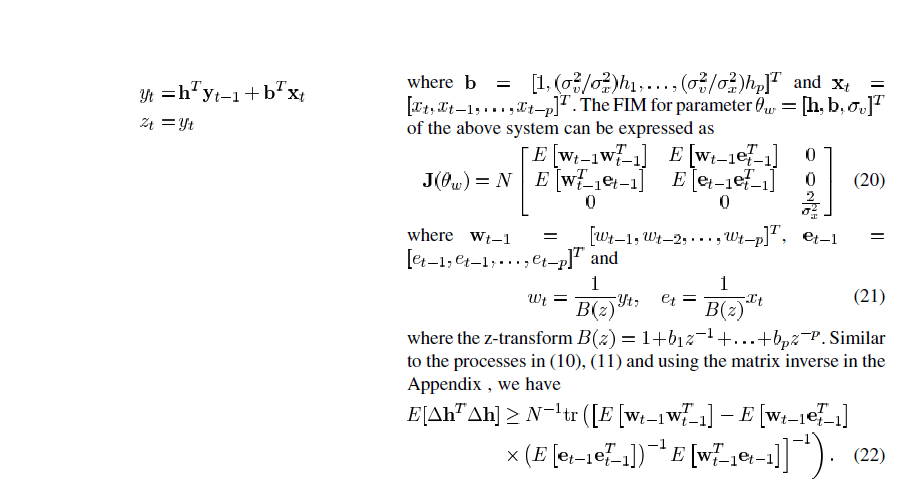

ОБНОВЛЕНИЕ: 01 декабря

В этом коде вопросы, аналитическая форма переменных

CRB_LHS = (b_transpose_b/N)*tr(inv(E[y(t-1)y(t-1)']))

CRB_RHS = sigma2_v*tr(inv(sum_t =1 to N E[y(t-1)y(t-1)']))

где у (т-1) =

[y(t-1), y(t-2),..,y(t-p)]'

CRB_LHS рассчитывается по формуле (19) статьи

`Y_ARMA(n)=  0.1950*Y_ARMA(n-1)- 0.1950*Y_ARMA(n-2) + b*x_gauss(n);` where

 x_gauss = N(0,1)

CRB_RHS рассчитывается по формуле (1)

Y_AR (n) = 0,1950*Y_AR(n-1) -0,9500*Y_AR(n-2) + x_chaos(n); где

x_chaos(n)= f(x(n-1),x(n-2),...,x(n-d)); d = 2

Я принял коэффициенты b = 1 для белого шума в модели ARMA уравнения (19).

Для каждого уровня SNR snrbd = -3:1:2 Я симулирую M количество временных рядов (M независимых прогонов). Есть 2 сомнения относительно реализации: (1) для RHS уравнения (25), в коде Ожидание берется за независимые прогоны (согласно предложению в ответе, если я правильно понял) - выражение показывает, что сумма берется по всем точкам данных и ожиданию по M выборкам для (t-1). Это сбивает с толку для реализации. (2) Код выдает ошибку из-за обратного. Невозможно решить это.

Результат должен быть CRB_LHS > CRB_RHS за каждый снар.

clc;
clear all;
N = 10;
M = 100;  % number of independent runs over which the 

  snrdb = -3:1:2;
for snr_levels = 1:length(snrdb)



for monte_carlo = 1: M
     x_gauss = randn(1,N);
     x_chaos(1) = rand();
% generate the chaotic code
    for i =1 : N
        x_chaos(i+1) = 4*x_chaos(i)*(1-x_chaos(i));
    end

    x_chaos = x_chaos-mean(x_chaos);
    Y_AR(1) = 0.0;
    Y_AR(2) = 0.0;

   Y_ARMA(1) = 0.0;
    Y_ARMA(2) = 0.0;
    for n= 3:N
    Y_ARMA(n)=  0.1950*Y_ARMA(n-1)- 0.1950*Y_ARMA(n-2) + x_gauss(n); %Eq(19) model
    Y_AR(n) =   0.1950*Y_AR(n-1) -0.9500*Y_AR(n-2)  + x_chaos(n); %Eq(1)
    end
    % signalPower_Y_AR = var(Y_AR);
 signalPower_Y_AR = 1;

    sigma2_v = signalPower_Y_AR .*(10^(-snrdb(snr_levels))) ;
    v = sqrt(sigma2_v)*randn(1,length(Y_AR));
    z = Y_AR + v;  %Eq(3)

Y_LHS = Y_ARMA(end-2:end-1).';
Y_RHS = z(end-2:end-1).';

A1(:,monte_carlo) = Y_LHS;
B1(monte_carlo,:) = Y_LHS.';

A2(:,monte_carlo) = Y_RHS;
B2(monte_carlo,:) = Y_RHS.';
end


dimension = length(Y_LHS);
sum_of_products_LHS = zeros(dimension,dimension);
sum_prod_RHS = zeros(dimension,dimension);

for runs = 1:M
A = A1(:,runs);
B = B1(runs,:);
mult_LHS = A*B;

C = A2(:,runs);
D = B2(runs,:);
mult_RHS = C*D;

sum_of_products_LHS = sum_of_products_LHS+ mult_LHS;
sum_of_products_RHS = sum_prod_RHS + mult_RHS;
end 

  b_transpose_b = 1;

Expectation_LHS = mean(sum_of_products_LHS);
% Inverse_LHS = inv(Expectation_LHS);
% trace_LHS = tr(Inverse_LHS);

Expectation_RHS = mean(sum_of_products_RHS);

% Inverse_RHS = inv(Expectation_RHS);
% trace_RHS = tr(Inverse_RHS);
%MANUALLY MAKING A SQUARE MATRIX
size_Inverse = 7;
InverseMatrix_LHS = eye(size_Inverse,size_Inverse);
InverseMatrix_RHS = eye(size_Inverse,size_Inverse);

for i = 1:size_Inverse
    InverseMatrix_LHS(i:size_Inverse,i) = Expectation_LHS(1:size_Inverse-i+1);
    InverseMatrix_LHS(i,i:size_Inverse) = Expectation_LHS(1:size_Inverse-i+1);

    InverseMatrix_RHS(i:size_Inverse,i) = Expectation_RHS(1:size_Inverse-i+1);
    InverseMatrix_RHS(i,i:size_Inverse) = Expectation_RHS(1:size_Inverse-i+1);

end
  trace_LHS = tr(InverseMatrix_LHS);
  CRLB_RHS(snr_levels)=  (b_transpose_b/N).*trace_RHS;

  trace_RHS = tr(InverseMatrix_RHS);
  CRLB_RHS(snr_levels)= sigma2_v*trace_RHS;

 end

Answer 1

Для p=2 выражение для y_tminus1 должно быть (см. Выражения после уравнения в статье)

y_tminus1 = Y(end-2:end-1).' 

Ваш мульт в порядке. Для уравнения 20 нужно принять ожидание E(мульт). Для этого вам нужно сгенерировать несколько путей и взять среднее по ним. Для RHS уравнения 25, вам нужно использовать y_tminus1 для каждого шага вашего процесса ARMA, суммировать соответствующие матрицы множеств, принимать ожидания по ансамблю и только после этого принимать обратное. Может быть, попробуйте настроить ваш код в соответствии с этими направлениями, и я исправлю это.