Chi Squared и уменьшенный Chi Squared = 0 с весами с использованием lmfit
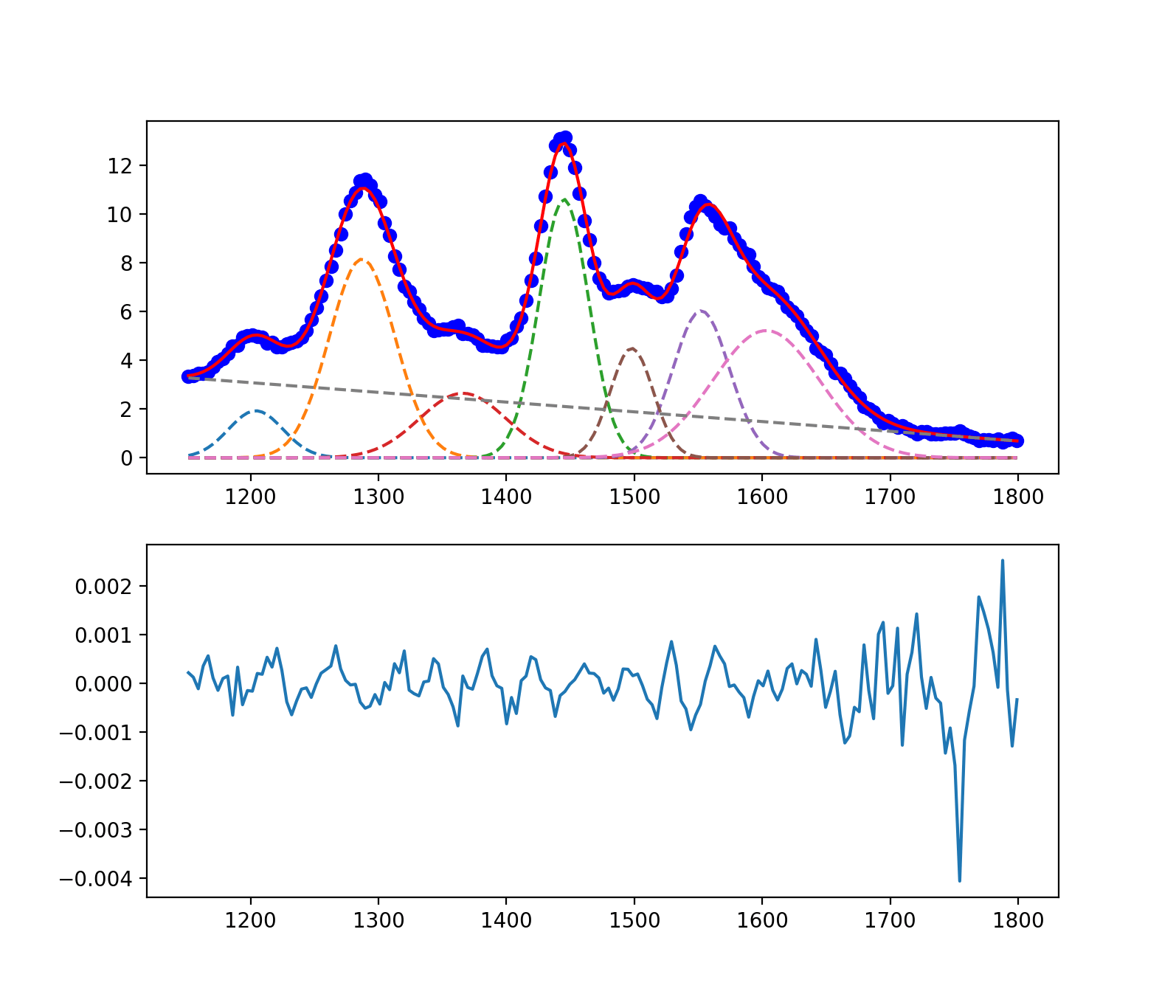
Я использую lmfit, чтобы соответствовать рамановским данным. Я использую 7 гауссовских пиков и линейный фон (5 из этих пиков известны, а два неизвестны). Я включил массив весов (обратный квадрат stdev). Когда я включаю веса - подгонка визуально выглядит намного лучше, а построенные остатки также имеют меньшую структуру, однако значения хи-квадрат и уменьшенные значения хи-квадрат сообщаются как 0. Я не уверен, что использую взвешивание оцените правильно, или, возможно, неправильно интерпретируете результаты. Я скопировал мой код ниже. Большое спасибо за любую помощь
x=[ 1151.41 1155.26 1159.11 1162.96 1166.8 1170.65 1174.5 1178.35
1182.19 1186.03 1189.88 1193.72 1197.57 1201.41 1205.25 1209.08
1212.92 1216.77 1220.6 1224.44 1228.27 1232.11 1235.94 1239.78
1243.61 1247.44 1251.27 1255.1 1258.94 1262.77 1266.6 1270.42
1274.25 1278.08 1281.91 1285.73 1289.55 1293.37 1297.2 1301.02
1304.84 1308.66 1312.48 1316.3 1320.12 1323.94 1327.75 1331.57
1335.39 1339.2 1343.01 1346.83 1350.64 1354.45 1358.26 1362.07
1365.88 1369.69 1373.49 1377.31 1381.11 1384.92 1388.72 1392.52
1396.33 1400.13 1403.93 1407.73 1411.53 1415.34 1419.13 1422.93
1426.73 1430.52 1434.32 1438.12 1441.91 1445.7 1449.49 1453.29
1457.08 1460.87 1464.66 1468.45 1472.24 1476.03 1479.81 1483.6
1487.38 1491.17 1494.96 1498.74]
y=[ 3.34835702 3.37753701 3.46421441 3.47561446 3.52906995
3.7430628 3.9445303 4.08069468 4.26772632 4.57141717
4.62653264 4.95543734 5.00090221 5.03820472 4.96421951
4.94593035 4.71712245 4.73136333 4.5449431 4.54198878
4.68326867 4.72099151 4.79832143 4.93313301 5.23041882
5.67948661 6.14714543 6.650372 7.289351 7.85672892
8.52692445 9.19116051 10.00674694 10.54570038 10.87682289
11.35534123 11.42260359 11.19421866 10.80316156 10.50632887
9.62797798 9.1298809 8.28793321 7.73275794 7.0211812
6.81838292 6.39480371 6.08652915 5.72148564 5.51527137
5.21654715 5.25030395 5.28647568 5.2812212 5.36064974
5.41940211 5.10942821 5.10866681 5.03248779 4.87465847
4.62568491 4.60337401 4.57096411 4.56132562 4.55625841
4.81601962 4.91783646 5.40526849 5.7393016 6.44435143
7.27609291 8.17028904 9.53128053 10.71589492 11.74175004
12.82955492 13.1016751 13.1616784 12.64563727 11.91554063
10.84031597 9.74302278 8.93611092 8.01037116 7.37684127
7.08713295 6.77556246 6.8143279 6.85773728 6.87895641
7.02718543 7.10869694]
weights=[ 0.01244515 0.0056474 0.00926648 0.00674491 0.00553186 0.00589553
0.00576142 0.00527653 0.00599983 0.00787368 0.00708644 0.00357355
0.00303342 0.00916585 0.00275235 0.00328612 0.00256573 0.00370105
0.00428572 0.00332175 0.00352448 0.00506917 0.00357058 0.00351362
0.0040452 0.00512055 0.00217692 0.00228909 0.00237594 0.00141826
0.00278388 0.00107677 0.00139026 0.00171414 0.0015294 0.00124306
0.00139236 0.00160101 0.00113102 0.00125891 0.00131655 0.00172122
0.00261752 0.00199811 0.00259736 0.00315851 0.00434901 0.00293013
0.00338841 0.00230605 0.00272563 0.00596109 0.00420324 0.00510059
0.00326837 0.00373911 0.00418471 0.00413105 0.00581997 0.0047461
0.00297461 0.00713362 0.00438222 0.00304455 0.00672188 0.00444613
0.00375129 0.00312274 0.00429026 0.00340182 0.00453605 0.00175878
0.0021822 0.0018159 0.0014724 0.00155655 0.00093935 0.00067046
0.00074241 0.00097113 0.0008329 0.00107734 0.00133742 0.00119752
0.00142113 0.00174815 0.00254059 0.0033123 0.0030637 0.00280913
0.00314901 0.00259063]
import os
import matplotlib.pyplot as plt
import pandas as pd
from lmfit.models import LinearModel
from lmfit.models import GaussianModel
import numpy as np
plotme = True
# import calibrated file
filename = 'file.csv'
data = pd.read_csv('file.csv', sep=",", index_col=[0], header=0)
samplename = os.path.splitext(os.path.basename(filename))[0]
# section out the data to use
data = data.set_index('x_ref', drop=False)
fingerprint = data[data.index > 1150]
fingerprint = fingerprint[fingerprint.index < 1500]
# define the x, y, and weights
x = x
y = y
wv = weights
lin_mod1 = LinearModel(prefix='lin1_')
pars = lin_mod1.guess(y, x=x)
gauss1 = GaussianModel(prefix='one_')
pars.update(gauss1.make_params())
pars['one_center'].set(1200)
pars['one_sigma'].set(2)
pars['one_amplitude'].set(10, min=0)
gauss2 = GaussianModel(prefix='two_')
pars.update(gauss2.make_params())
pars['two_center'].set(1275)
pars['two_sigma'].set(2)
pars['two_amplitude'].set(10, min=0)
gauss3 = GaussianModel(prefix='three_')
pars.update(gauss3.make_params())
pars['three_center'].set(1450)
pars['three_sigma'].set(2)
pars['three_amplitude'].set(10, min=0)
gauss4 = GaussianModel(prefix='unknown_')
pars.update(gauss4.make_params())
pars['unknown_center'].set(1355)
pars['unknown_sigma'].set(2)
pars['unknown_amplitude'].set(10, min=0)
gauss5 = GaussianModel(prefix='unknown2_')
pars.update(gauss5.make_params())
pars['unknown2_center'].set(1510)
pars['unknown2_sigma'].set(2)
pars['unknown2_amplitude'].set(10, min=0)
gauss6 = GaussianModel(prefix='six_')
pars.update(gauss6.make_params())
pars['six_center'].set(1550)
pars['six_sigma'].set(2)
pars['six_amplitude'].set(10, min=0)
gauss7 = GaussianModel(prefix='seven_')
pars.update(gauss7.make_params())
pars['seven_center'].set(1600)
pars['seven_sigma'].set(2)
pars['seven_amplitude'].set(10, min=0)
mod = gauss1 + gauss2 + gauss3 + gauss4 + gauss5 + gauss6 + gauss7 + lin_mod1
init = mod.eval(pars, x=x)
out = mod.fit(y, pars, x=x, weights=wv)
print(out.fit_report())
if plotme:
plt.subplot(2, 1, 1)
plt.plot(x, y, 'bo')
# plt.plot(x, init, 'k--')
plt.plot(x, out.best_fit, 'r-')
comps = out.eval_components(x=x)
plt.plot(x, comps['one_'], '--')
plt.plot(x, comps['two_'], '--')
plt.plot(x, comps['three_'], '--')
plt.plot(x, comps['unknown_'], '--')
plt.plot(x, comps['six_'], '--')
plt.plot(x, comps['unknown2_'], '--')
plt.plot(x, comps['seven_'], '--')
plt.plot(x, comps['lin1_'], '--')
plt.subplot(2, 1, 2)
plt.title('residuals')
plt.plot(x, out.residual, '-')
plt.subplots_adjust(top=0.95, bottom=0.10, left=0.10, right=0.95, hspace=0.50, wspace=0.35)
plt.show()
вывод, включая веса:
[[Model]]
(((((((Model(gaussian, prefix='one_') + Model(gaussian, prefix='two_')) + Model(gaussian, prefix='three_')) + Model(gaussian, prefix='unknown_')) + Model(gaussian, prefix='unknown2_')) + Model(gaussian, prefix='six_')) + Model(gaussian, prefix='seven_')) + Model(linear, prefix='lin1_'))
[[Fit Statistics]]
# function evals = 366
# data points = 172
# variables = 23
chi-square = 0.000
reduced chi-square = 0.000
Akaike info crit = -2481.840
Bayesian info crit = -2409.448
[[Variables]]
lin1_intercept: 7.87347446 +/- 0.202758 (2.58%) (init= 16.00284)
lin1_slope: -0.00399367 +/- 0.000115 (2.88%) (init=-0.006952215)
one_sigma: 21.2666157 +/- 1.423474 (6.69%) (init= 2)
one_center: 1204.02129 +/- 1.132164 (0.09%) (init= 1200)
one_amplitude: 102.715569 +/- 9.153523 (8.91%) (init= 10)
one_fwhm: 50.0790521 +/- 3.352026 (6.69%) == '2.3548200*one_sigma'
one_height: 1.92685033 +/- 0.073258 (3.80%) == '0.3989423*one_amplitude/max(1.e-15, one_sigma)'
two_sigma: 25.7977895 +/- 0.871817 (3.38%) (init= 2)
two_center: 1287.20816 +/- 1.068676 (0.08%) (init= 1275)
two_amplitude: 527.208091 +/- 24.04663 (4.56%) (init= 10)
two_fwhm: 60.7491508 +/- 2.052973 (3.38%) == '2.3548200*two_sigma'
two_height: 8.15285388 +/- 0.212054 (2.60%) == '0.3989423*two_amplitude/max(1.e-15, two_sigma)'
three_sigma: 19.5097449 +/- 0.798387 (4.09%) (init= 2)
three_center: 1444.94305 +/- 0.757566 (0.05%) (init= 1450)
three_amplitude: 518.683054 +/- 24.82361 (4.79%) (init= 10)
three_fwhm: 45.9419376 +/- 1.880058 (4.09%) == '2.3548200*three_sigma'
three_height: 10.6062181 +/- 0.249698 (2.35%) == '0.3989423*three_amplitude/max(1.e-15, three_sigma)'
unknown_sigma: 33.8695907 +/- 4.913019 (14.51%) (init= 2)
unknown_center: 1365.89866 +/- 2.572737 (0.19%) (init= 1355)
unknown_amplitude: 224.557732 +/- 33.37427 (14.86%) (init= 10)
unknown_fwhm: 79.7567896 +/- 11.56927 (14.51%) == '2.3548200*unknown_sigma'
unknown_height: 2.64501508 +/- 0.077333 (2.92%) == '0.3989423*unknown_amplitude/max(1.e-15, unknown_sigma)'
unknown2_sigma: 16.8566531 +/- 1.909319 (11.33%) (init= 2)
unknown2_center: 1497.93496 +/- 1.297153 (0.09%) (init= 1510)
unknown2_amplitude: 189.598971 +/- 27.39291 (14.45%) (init= 10)
unknown2_fwhm: 39.6943839 +/- 4.496103 (11.33%) == '2.3548200*unknown2_sigma'
unknown2_height: 4.48719263 +/- 0.196189 (4.37%) == '0.3989423*unknown2_amplitude/max(1.e-15, unknown2_sigma)'
six_sigma: 22.0949199 +/- 2.010271 (9.10%) (init= 2)
six_center: 1552.18018 +/- 1.324973 (0.09%) (init= 1550)
six_amplitude: 333.936881 +/- 54.65493 (16.37%) (init= 10)
six_fwhm: 52.0295593 +/- 4.733827 (9.10%) == '2.3548200*six_sigma'
six_height: 6.02951031 +/- 0.537614 (8.92%) == '0.3989423*six_amplitude/max(1.e-15, six_sigma)'
seven_sigma: 41.8944271 +/- 1.648292 (3.93%) (init= 2)
seven_center: 1603.04249 +/- 4.014783 (0.25%) (init= 1600)
seven_amplitude: 547.973799 +/- 48.61137 (8.87%) (init= 10)
seven_fwhm: 98.6538348 +/- 3.881433 (3.93%) == '2.3548200*seven_sigma'
seven_height: 5.21811474 +/- 0.274354 (5.26%) == '0.3989423*seven_amplitude/max(1.e-15, seven_sigma)'
[[Correlations]] (unreported correlations are < 0.100)
C(lin1_intercept, lin1_slope) = -0.999
C(seven_center, seven_amplitude) = -0.987
C(unknown_sigma, unknown_amplitude) = 0.980
C(unknown2_sigma, unknown2_amplitude) = 0.971
C(seven_sigma, seven_center) = -0.966
C(seven_sigma, seven_amplitude) = 0.953
C(six_amplitude, seven_amplitude) = -0.946
C(six_amplitude, seven_center) = 0.935
C(one_sigma, one_amplitude) = 0.920
C(six_sigma, six_amplitude) = 0.910
C(two_amplitude, unknown_sigma) = -0.900
C(two_amplitude, unknown_amplitude) = -0.896
C(two_center, unknown_amplitude) = -0.886
C(two_center, unknown_sigma) = -0.880
C(six_amplitude, seven_sigma) = -0.877
C(three_sigma, three_amplitude) = 0.871
C(two_center, two_amplitude) = 0.858
C(lin1_intercept, one_amplitude) = -0.844
C(lin1_slope, one_amplitude) = 0.839
C(two_sigma, two_amplitude) = 0.826
C(two_sigma, unknown_center) = 0.820
C(two_sigma, unknown_amplitude) = -0.813
C(two_amplitude, unknown_center) = 0.805
C(two_center, unknown_center) = 0.799
C(six_sigma, seven_amplitude) = -0.784
C(two_sigma, unknown_sigma) = -0.764
C(lin1_intercept, one_sigma) = -0.758
C(six_sigma, seven_center) = 0.754
C(lin1_slope, one_sigma) = 0.754
C(three_amplitude, unknown2_amplitude) = -0.748
C(two_sigma, two_center) = 0.737
C(unknown_center, unknown_amplitude) = -0.731
C(three_amplitude, unknown2_sigma) = -0.717
C(three_center, unknown2_amplitude) = -0.713
C(three_center, unknown2_sigma) = -0.705
C(three_sigma, unknown2_amplitude) = -0.696
C(unknown_sigma, unknown_center) = -0.688
C(unknown2_amplitude, six_sigma) = -0.682
C(unknown2_amplitude, six_center) = 0.681
C(unknown2_sigma, six_center) = 0.675
C(six_sigma, seven_sigma) = -0.671
C(three_sigma, unknown_sigma) = -0.662
C(three_amplitude, unknown_sigma) = -0.660
C(unknown2_sigma, six_sigma) = -0.653
C(three_sigma, unknown2_sigma) = -0.643
C(three_sigma, unknown_amplitude) = -0.640
C(three_amplitude, unknown_amplitude) = -0.631
C(three_center, three_amplitude) = 0.621
C(one_center, two_sigma) = -0.620
C(three_sigma, three_center) = 0.548
C(two_amplitude, three_amplitude) = 0.542
C(unknown2_sigma, six_amplitude) = -0.539
C(unknown2_amplitude, six_amplitude) = -0.533
C(two_amplitude, three_sigma) = 0.518
C(two_center, three_amplitude) = 0.517
C(one_amplitude, two_sigma) = -0.497
C(two_center, three_sigma) = 0.494
C(one_sigma, two_sigma) = -0.484
C(unknown2_center, six_sigma) = -0.483
C(one_center, two_amplitude) = -0.468
C(one_amplitude, unknown_amplitude) = 0.442
C(one_sigma, one_center) = 0.431
C(one_center, one_amplitude) = 0.422
C(three_sigma, unknown2_center) = 0.416
C(one_center, unknown_center) = -0.414
C(one_sigma, unknown_amplitude) = 0.408
C(two_sigma, three_amplitude) = 0.406
C(three_center, six_center) = -0.404
C(three_amplitude, six_center) = -0.398
C(two_sigma, three_sigma) = 0.383
C(unknown2_center, six_amplitude) = -0.374
C(one_center, unknown_amplitude) = 0.364
C(three_amplitude, unknown2_center) = 0.358
C(three_center, six_sigma) = 0.356
C(one_amplitude, unknown_center) = -0.349
C(three_amplitude, six_sigma) = 0.348
C(three_sigma, six_center) = -0.340
C(one_center, unknown_sigma) = 0.337
C(unknown_sigma, unknown2_amplitude) = 0.333
C(unknown_amplitude, unknown2_amplitude) = 0.332
C(one_sigma, unknown_center) = -0.329
C(one_amplitude, unknown_sigma) = 0.324
C(unknown2_sigma, seven_amplitude) = 0.321
C(unknown2_amplitude, seven_amplitude) = 0.309
C(three_center, six_amplitude) = 0.301
C(one_sigma, unknown_sigma) = 0.300
C(unknown2_sigma, seven_center) = -0.297
C(three_amplitude, six_amplitude) = 0.296
C(three_sigma, six_sigma) = 0.294
C(unknown_sigma, unknown2_sigma) = 0.291
C(unknown_amplitude, unknown2_sigma) = 0.288
C(lin1_intercept, unknown_amplitude) = -0.286
C(lin1_slope, unknown_amplitude) = 0.284
C(unknown2_amplitude, seven_center) = -0.278
C(three_center, unknown2_center) = 0.277
C(one_sigma, two_amplitude) = -0.276
C(one_amplitude, two_amplitude) = -0.275
C(unknown2_center, seven_amplitude) = 0.272
C(unknown2_center, six_center) = 0.265
C(unknown2_center, seven_center) = -0.254
C(three_sigma, six_amplitude) = 0.252
C(unknown2_sigma, seven_sigma) = 0.249
C(two_amplitude, unknown2_amplitude) = -0.245
C(two_center, unknown2_amplitude) = -0.238
C(unknown_sigma, unknown2_center) = -0.237
C(three_amplitude, unknown_center) = 0.237
C(unknown_amplitude, unknown2_center) = -0.228
C(unknown2_amplitude, seven_sigma) = 0.225
C(six_sigma, six_center) = -0.220
C(two_amplitude, unknown2_sigma) = -0.215
C(six_center, seven_center) = 0.212
C(one_amplitude, seven_sigma) = 0.211
C(one_center, two_center) = -0.208
C(two_center, unknown2_sigma) = -0.207
C(unknown2_center, seven_sigma) = 0.207
C(lin1_intercept, seven_sigma) = -0.205
C(six_center, seven_sigma) = -0.205
C(six_center, seven_amplitude) = -0.205
C(one_amplitude, two_center) = -0.201
C(one_amplitude, seven_amplitude) = 0.190
C(lin1_intercept, two_sigma) = 0.189
C(one_sigma, seven_sigma) = 0.188
C(lin1_slope, two_sigma) = -0.188
C(two_sigma, unknown2_amplitude) = -0.187
C(lin1_slope, seven_sigma) = 0.186
C(lin1_intercept, seven_amplitude) = -0.185
C(two_amplitude, unknown2_center) = 0.183
C(two_center, unknown2_center) = 0.173
C(one_center, three_amplitude) = -0.173
C(one_sigma, seven_amplitude) = 0.170
C(three_center, seven_amplitude) = -0.170
C(lin1_slope, seven_amplitude) = 0.169
C(one_sigma, two_center) = -0.166
C(three_amplitude, seven_amplitude) = -0.166
C(lin1_intercept, unknown_sigma) = -0.164
C(lin1_slope, unknown_sigma) = 0.163
C(three_sigma, unknown_center) = 0.162
C(two_sigma, unknown2_sigma) = -0.161
C(three_center, seven_center) = 0.160
C(one_center, three_sigma) = -0.157
C(three_amplitude, seven_center) = 0.156
C(lin1_intercept, unknown_center) = 0.146
C(lin1_slope, unknown_center) = -0.146
C(one_amplitude, seven_center) = -0.145
C(three_sigma, seven_amplitude) = -0.145
C(unknown_amplitude, six_sigma) = -0.141
C(unknown_amplitude, six_amplitude) = -0.137
C(unknown_sigma, six_center) = 0.136
C(lin1_intercept, seven_center) = 0.135
C(three_center, unknown_center) = -0.135
C(three_sigma, seven_center) = 0.134
C(unknown_sigma, six_sigma) = -0.133
C(three_center, seven_sigma) = -0.132
C(two_sigma, unknown2_center) = 0.132
C(three_amplitude, seven_sigma) = -0.130
C(one_sigma, seven_center) = -0.130
C(unknown_amplitude, six_center) = 0.126
C(one_amplitude, three_sigma) = -0.123
C(one_amplitude, six_amplitude) = -0.122
C(unknown_sigma, six_amplitude) = -0.122
C(lin1_slope, seven_center) = -0.121
C(unknown_amplitude, seven_amplitude) = 0.118
C(three_sigma, seven_sigma) = -0.116
C(unknown_amplitude, seven_sigma) = 0.114
C(one_sigma, three_sigma) = -0.113
C(unknown2_center, unknown2_amplitude) = 0.111
C(one_sigma, six_amplitude) = -0.109
C(unknown2_sigma, unknown2_center) = 0.109
C(one_amplitude, unknown2_amplitude) = 0.107
C(two_amplitude, six_center) = -0.107
C(lin1_intercept, six_amplitude) = 0.105
C(lin1_intercept, two_center) = 0.101
1 ответ
Отчет о статистике хи-квадрат ограничен 3 цифрами в используемой вами версии. Я считаю, что это было исправлено в самой последней версии (0.9.9) и определенно исправлено в последней версии для разработчиков. Вы также можете распечатать значения с большей точностью самостоятельно:
print("chi-square = %14.8g, reduced chi-square = %14.8g" % (out.chisqr, out.redchi))
Но также: я думаю, что использование весов "обратного квадрата стандартного значения" может оказаться не тем, что вы хотите. Для ясности, веса являются мультипликативным коэффициентом, применяемым к (модель данных), и тогда хи-квадрат будет равен "Сумма [(модель данных)* веса]**2". Поэтому я думаю, что использование "weight = 1./(stddev of data)" (то есть не в квадрате) является наиболее распространенным подходом для данных, которые, как ожидается, будут нормально распределены, и ваши рамановские данные, вероятно, по крайней мере в ощущение отсутствия сигнала с преобладанием подсчета небольших чисел (где предпочтительнее статистика Poission).
Надеюсь, это поможет.