Самая длинная подпоследовательность в прологе

Question

Я хочу реализовать предикат P(Xs,Ys,Zs) где Xs,Ys,Zs являются списками.

Я новичок в Прологе и не могу найти способ добраться до самой длинной последовательности в Xs (пример. Xs = ['b','b','A','A','A','A','b','b']) который включен в Ys (например Ys = ['A','A','A','A','c','A','A','A','A']без пересечения - четное количество раз. Может быть, кто-то уже написал этот код или кто-то может сказать мне, как я могу начать. Спасибо за помощь.

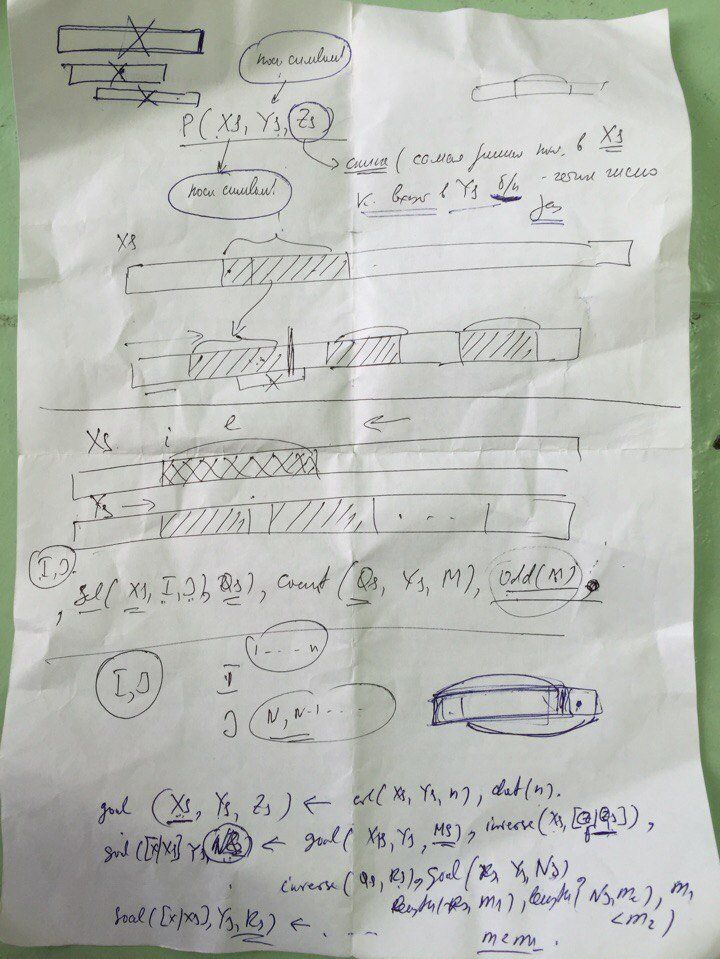объяснение учителя.

longest_subsequence(List, Part, Subsequence):-
    longest_subsequence_(List, Part, [], Subsequence).

longest_subsequence_(Xs, Ys, CurrentSubsequence, LongestSubsequence):-
    append(CurrentSubsequence, Ys, NextSubsequence),
    divide_list(Xs, [_LeftYs, NextSubsequence, _RightYs]), !,
    longest_subsequence_(Xs, Ys, NextSubsequence, LongestSubsequence).
longest_subsequence_(_Xs, _Ys, LongestSubsequence, LongestSubsequence).

Answer 1

Хорошо, я сделал.

 main_task(Xs, Ys, Zs) :-         
      atom_chars(Xs, Xl),
      atom_chars(Ys, Yl),
      retractall(record(_, _)),
      assert(record(0, [])),
      process(Xl, Yl, Zl),
      atom_chars(Zs, Zl).

 process(Xl, Yl, _) :-     
      get_sublist(Xl, Zl),     
      length(Zl, L),
      record(MaxL, _),
      L > MaxL,
      get_index(Yl, Zl, Il),
      test_even(Il),
      test_intersect(Il, L),
      retractall(record(_, _)),
      assert(record(L, Zl)),
      fail.
    process(_, _, Zl) :-
      record(_, Zl).

    get_sublist(L1, L2) :-
      get_tail(L1, L3),
      get_head(L3, L2).

    get_tail(L, L).
    get_tail([_|T], L) :-
        get_tail(T, L).

    get_head([H|T1], [H|T2]) :-
        get_head(T1, T2).
    get_head(_, []).

    get_index(Yl, Zl, Il) :-
      get_index(Yl, Zl, Il, 0).

    get_index([], _, [], _).
    get_index([Yh|Yt], Zl, [I|It], I) :-
      get_head([Yh|Yt], Zl),
      !,
      I1 is I + 1,
      get_index(Yt, Zl, It, I1).
    get_index([_|Yt], Zl, Il, I) :-
      I1 is I + 1,
      get_index(Yt, Zl, Il, I1).

    test_even(Il) :-
      length(Il, L),
      L > 0,
      L mod 2 =:= 0.

    test_intersect([_], _).
    test_intersect([X,Y|T], L) :-
      Y - X >= L,
      test_intersect([Y|T], L).

1. Все строки в списке по символам при работе со списками
2. Инициализировать динамическую базу данных - в ней будет храниться максимальная длина строки
3. перечисляет все подстроки (подсписки) из X. Бюст проходит двойную "обрезку" - сначала в списке обрезанных спереди, затем сзади.
4. Проверьте длину полученной строки, если у нас уже есть длинная, немедленно оставьте для продолжения перебора
5. Мы рассматриваем список индексов в появлении Y, тогда есть каждый элемент списка - позиция в Y, из которой он включает Z.
6. Проверьте четность - просто рассмотрите длину списка индексов, чётная длина - четное количество записей. И нам нужно проверить, что оно больше нуля.
7. Проверьте пересечение - вам нужно проверить разницу между двумя смежными элементами списка индексов, разница всегда должна быть больше длины Z.
8. Если все проверки сделаны, происходит динамическое обновление базы данных - текущий список Z сохраняется как максимум
9. В конце концов это вынужденный сбой, он откатывается до развилки в пункте 3) и продолжается поиск. Примечание: Если какая-либо проверка не выполняется, сбой этого теста немедленно откатывается до развилки в параграфе 3) и продолжается поиск.
10. Когда бюст подходит к концу, выполняется второй процесс предиката правила, он просто выбирает последний всплеск Z в базе.
11. В конце списка Z преобразуется обратно в строку

Answer 2

При приближении к проблеме сначала попробуйте: разделяй и властвуй.

Когда у нас есть list_subsequence(+List, ?Subsequence) сказуемое

list_subsequence([H|T], S) :-
  list_subsequence(H, T, S, _).
list_subsequence([H|T], S) :-
  list_subsequence(H, T, _, R),
  list_subsequence(R, S).

list_subsequence(H, [H|T], [H|S], R) :- !, list_subsequence(H, T, S, R).
list_subsequence(H, R, [H], R).

мы можем вызвать библиотечную ( совокупную) помощь:

longest_subsequence(Seq, Rep, Longest) :-
  aggregate(max(L, Sub), N^(
    list_subsequence(Seq, Sub),
    aggregate(count, list_subsequence(Rep, Sub), N),
    N mod 2 =:= 0,
    length(Sub, L)
  ), max(_, Longest)).

Answer 3

Наивный подход заключается в следующем:

longest_subsequence(Xs,Ys,Zs) :-
    longest_subsequence(Xs,Ys,Ys,0,[],Zs).

longest_subsequence([X|Xs],Y0,[Y|Ys],N0,Z0,Z) :-
    try_seq([X|Xs],[Y|Ys],Nc,Zc),
    (Nc > N0
    -> longest_subsequence([X|Xs],Y0,Ys,Nc,Zc,Z)
    ;  longest_subsequence([X|Xs],Y0,Ys,N0,Z0,Z)
    ).
longest_subsequence([_|Xs],Y0,[],N0,Z0,Z) :-
    longest_subsequence(Xs,Y0,Y0,N0,Z0,Z).
longest_subsequence([],_,_,_,Z,Z).

try_seq([H|TA],[H|TB],N,[H|TC]) :-
    !,
    try_seq(TA,TB,N1,TC),
    N is N1+1.
try_seq(_,_,0,[]).

здесь предикат try_seq/3 стремится максимально соответствовать (генерирует самую длинную общую подпоследовательность), начиная с начала списка.

Проблема заключается в том, что это вычислительно дорогой подход: он будет иметь временную сложность O(m n p) с n длиной первого списка, m длиной второго списка и p минимальной длиной двух списков.

Вызов этого в вашем примере дает:

?- longest_subsequence([b,b,a,a,a],[a,a,a,c,a,a,a],Zs).
Zs = [a, a, a] ;
false.

Вы можете сделать алгоритм более эффективным, используя обратные ссылки, более или менее основанные на алгоритме Кнута-Морриса-Пратта.