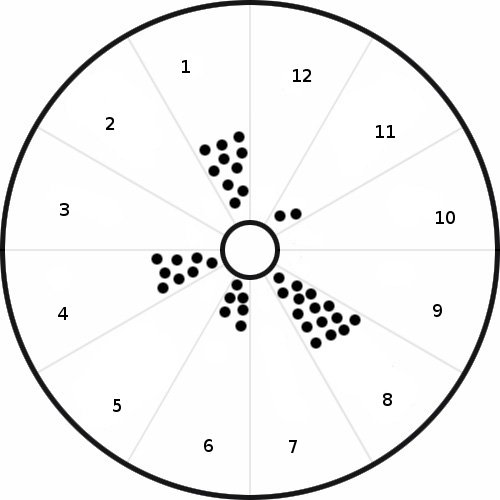
Расположите точки в определенных секторах круга, начиная с центра
Проблема заключается в расположении точек в определенных секторах круга, начиная с центра.
$ dot [1] = secto12; $ dot [2] = secto6; $ dot [3] = secto8; $ dot [4] = secto2; $ dot [5] = secto8; $ dot [6] = secto3; так далее...
Мы могли бы использовать PHP или JavaScript.
Я могу представить себе функцию, имитирующую центростремительную силу. Или, может быть, какая-то процедура аналитической геометрии. Или что угодно...
Любая идея приветствуется. СПАСИБО.-
5 ответов

Решение, которое я использовал, немного сложнее. И не является общим. Нам нужно вычислить определенные вещи вручную ($factor (вариации углов) и $dots (количество точек для рисования на определенном радиусе)).
Но я хочу дать основные идеи для кого-то, кому нужно нечто подобное:
1. Мы используем уравнение, которое находит заданную точку:
0.- центральная точка: ($ x0, $ y0)
1.- радиус: $ r
2.- угол: $ угол
$x = floor($x0 + $r * sin($angle * pi() / 180));
$y = floor($y0 + $r * -cos($angle * pi() / 180));
2.-Мы строим точки (определенное количество точек), меняя радиус и угол
Количество точек зависит от радиуса. Больше радиуса, больше точек. Нам нужно определить функцию, которая рисует точки сектор за сектором.
3. Нам нужно вычислить определенные вещи вручную ($factor (вариации углов) и $dots (количество точек для рисования на определенном радиусе)). Вот:
if ($r >= 90) {
$dots = 4;
$factor = 12.1;
}
if ($r >= 100) {
$dots = 4;
$factor = 12.4;
}
if ($r >= 110) {
$dots = 5;
$factor = 8.4;
}
if ($r >= 120) {
$dots = 6;
$factor = 6.2;
}
if ($r >= 130) {
$dots = 7;
$factor = 5.2;
}
if ($r >= 140) {
$dots = 8;
$factor = 4.4;
}
if ($r >= 150) {
$dots = 9;
$factor = 3.8;
}
if ($r >= 200) {
$dots = 10;
$factor = 3.40;
}
if ($r >= 220) {
$dots = 11;
$factor = 3.0;
}
Это основные идеи, чтобы решить это, хитрым способом.
4. Очевидно, что этот код (внутри функции) должен вызываться внутри вложенных циклов (3 в моем случае)
function plot($sector, $start) {
....
}
$ start - угол от начала рисования: 0, 30, 60,..., 330
??? ОК, вот функция. Наслаждаться:
function plot($sector, $start) {
static $static;
$x0 = 0;
$y0 = 0;
if ( ! isset($static[$sector])) {
/*
* factor: related to the amplitude of the arc on which dots are drawn. (11.1 -> 3.0)
* dots: how many dots draw towards the right. (3 -> 10)
* r: radius in pixels. (60 -> 240)
* jstatic: save last position of dot drawn.
*
*/
$static[$sector]['factor'] = 11.1;
$static[$sector]['dots'] = 4;
$static[$sector]['r'] = 60;
$static[$sector]['jstatic'] = 0;
}
$factor = $static[$sector]['factor'];
$dots = $static[$sector]['dots'];
$r = $static[$sector]['r'];
$jstatic = $static[$sector]['jstatic'];
for ($j = $jstatic; $j < $dots; $j ++ ) {
if ($r >= 90) {
$dots = 4;
$factor = 12.1;
}
if ($r >= 100) {
$dots = 4;
$factor = 12.4;
}
if ($r >= 110) {
$dots = 5;
$factor = 8.4;
}
if ($r >= 120) {
$dots = 6;
$factor = 6.2;
}
if ($r >= 130) {
$dots = 7;
$factor = 5.2;
}
if ($r >= 140) {
$dots = 8;
$factor = 4.4;
}
if ($r >= 150) {
$dots = 9;
$factor = 3.8;
}
if ($r >= 200) {
$dots = 10;
$factor = 3.40;
}
if ($r >= 220) {
$dots = 11;
$factor = 3.0;
}
if ($j == $dots - 1) {
$j = 0;
$jstatic = 0;
// increase radius (by 10 pixels --each dot have 7 pixel of diameter) to the next arc.
$r = $r + 10;
}
// stop if circumference is reached.
if ($r > 240)
break;
$angle = $factor * $j + $start;
// (x, y) is...
$x = floor($x0 + $r * sin($angle * pi() / 180));
$y = floor($y0 + $r * -cos($angle * pi() / 180));
$pos['x'] = $x;
$pos['y'] = $y;
$jstatic ++;
// save all dat by each sector
$static[$sector]['factor'] = $factor;
$static[$sector]['dots'] = $dots;
$static[$sector]['r'] = $r;
$static[$sector]['jstatic'] = $jstatic;
/*
* only for debugging:
* counting how many dots are drawn
static $countDots = 0;
global $countDots;
$countDots++;
*/
return $pos;
}
}
Проблема найти место, где точка останавливается, довольно сложна, но я думаю, что я бы подошел к этому так (с экспериментами на этом пути, чтобы поддержать интуицию):
- Выберите начальную тэту наугад в пределах желаемой корзины. Это расположение точки на "вершине" (краю круга).
- Для каждой точки, уже находящейся в ячейке, определите ее (угловое) расстояние до выбранной линии падения. Тогда простая геометрия - определить, с какой точкой будет сталкиваться падающая точка, и где она будет находиться, когда это произойдет. Этого достаточно для снежинок.
- Мрамор может скользить; посмотрите на соседей по неподвижной точке, со стороны которой касалась падающая точка. Мы можем определить, с каким соседом скользящая точка встретится первой. Смотреть на стены. (Мы не будем беспокоиться о том, чтобы подпрыгивать, смещать стационарные точки или становиться в воздухе - сим не должен быть таким хорошим.)
- Если скользящая точка соприкасается с соседом на противоположной стороне, она останавливается. Если он вступает в контакт с той же стороны, он может свободно скользить по соседу - мы должны повторить предыдущий шаг.
PS Это даст довольно хорошую упаковку, которая, вероятно, все, что вам нужно. Оптимальную упаковку действительно сложно найти.
Здесь есть две половины: математика позиционирования точек и механизм рендеринга для отображения круга + точек.
Первая половина - интересная математическая головоломка, которая, вероятно, выходит за рамки простого вопроса переполнения стека. Но как только вы настроите систему рендеринга, вы можете легко экспериментировать, пока не добьетесь того, что ищете.
Во второй половине я предлагаю изучить Raphael, библиотеку Javascript для простого рисования фигур и другой векторной графики с использованием SVG.
Это довольно просто решить с помощью sfc, или кривой Гильберта, или кода Грея. На самом деле кривая Гильберта является гамильтоновым обходом графа, и таким образом генерируется серый код. Вы можете искать в сети информацию о сером коде и о том, как он используется для правильного определения секторов на жестком диске. Если для решения задачи использовать кривую Гильберта, то ее ограничения заключаются в том, что окружность должна покрывать плоскость степени 2. Другая проблема состоит в том, что она является только приближенной, но очень хорошей.
Построить физический движок для симуляции кругов и стен, хотя это и сложнее, чем вы ожидали, не так уж сложно. Если вы используете интеграцию Verlet для контроля местоположения и скорости движения шариков, столкновения между шариками и между шариками и стенками сегмента становятся тривиально простыми - вы просто перемещаете оскорбительные шарики на минимальное расстояние, необходимое для разрешения столкновения. Ответ на столкновение - потеря скорости и т. Д. Обрабатывается неявно.
Вы бы настроили свою систему так, чтобы шарики были притянуты к центру круга и были вынуждены остаться:
- Некоторое расстояние от центра
- В их сегменте
- На некотором расстоянии от других шаров
Простое физическое моделирование обеспечит хорошую упаковку для шаров, и вы получите классную анимацию бесплатно.
Это хорошее объяснение подхода (все до раздела "Жесткие тела" уместно)