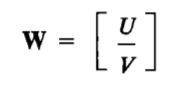Простая орфографическая структура из движения с использованием R - определение метрических ограничений

Question

Простая орфографическая структура из движения с использованием R - определение метрических ограничений

Я хотел бы построить простую структуру из программы движения в соответствии с Томаси и Канаде [1992]. Статью можно найти ниже:

https://people.eecs.berkeley.edu/~yang/courses/cs294-6/papers/TomasiC_Shape%20and%20motion%20from%20image%20streams%20under%20orthography.pdf

Этот метод кажется элегантным и простым, однако у меня возникают проблемы с вычислением метрических ограничений, изложенных в уравнении 16 вышеупомянутой ссылки.

Я использую R и обрисовал в общих чертах мою работу до сих пор:

Учитывая набор изображений

Я хочу отслеживать углы трех дверей шкафа и одной картинки (черные точки на изображениях). Сначала мы читаем в точках в виде матрицы W, где

В конечном счете, мы хотим разложить w на матрицу вращения R и матрицу формы S, которые описывают трехмерные точки. Я сэкономлю столько деталей, сколько смогу, но полное описание математики можно почерпнуть из статьи Томаси и Канаде [1992].

Я поставляю ш ниже:

w.vector=c(0.2076,0.1369,0.1918,0.1862,0.1741,0.1434,0.176,0.1723,0.2047,0.233,0.3593,0.3668,0.3744,0.3593,0.3876,0.3574,0.3639,0.3062,0.3295,0.3267,0.3128,0.2811,0.2979,0.2876,0.2782,0.2876,0.3838,0.3819,0.3819,0.3649,0.3913,0.3555,0.3593,0.2997,0.3202,0.3137,0.31,0.2718,0.2895,0.2867,0.825,0.7703,0.742,0.7251,0.7232,0.7138,0.7345,0.6911,0.1937,0.1248,0.1723,0.1741,0.1657,0.1313,0.162,0.1657,0.8834,0.8118,0.7552,0.727,0.7364,0.7232,0.7288,0.6892,0.4309,0.3798,0.4021,0.3965,0.3844,0.3546,0.3695,0.3583,0.314,0.3065,0.3989,0.3876,0.3857,0.3781,0.3989,0.3593,0.5184,0.4849,0.5147,0.5193,0.5109,0.4812,0.4979,0.4849,0.3536,0.3517,0.4121,0.3951,0.3951,0.3781,0.397,0.348,0.5175,0.484,0.5091,0.5147,0.5128,0.4784,0.4905,0.4821,0.7722,0.7326,0.7326,0.7232,0.7232,0.7119,0.7402,0.7006,0.4281,0.3779,0.3918,0.3863,0.3825,0.3472,0.3611,0.3537,0.8043,0.7628,0.7458,0.7288,0.727,0.7213,0.7364,0.6949,0.5789,0.5491,0.5761,0.5817,0.5733,0.5444,0.5537,0.5379,0.3649,0.3536,0.4177,0.3951,0.3857,0.3819,0.397,0.3461,0.697,0.671,0.6821,0.6821,0.6719,0.6412,0.6468,0.6235,0.3744,0.3649,0.4159,0.3819,0.3781,0.3612,0.3763,0.314,0.7008,0.6691,0.6794,0.6812,0.6747,0.6393,0.6412,0.6235,0.7571,0.7345,0.7439,0.7496,0.7402,0.742,0.7647,0.7213,0.5817,0.5463,0.5696,0.5779,0.5761,0.5398,0.551,0.5398,0.7665,0.7326,0.7439,0.7345,0.7288,0.727,0.7515,0.7062,0.8301,0.818,0.8571,0.8878,0.8766,0.8561,0.858,0.8394,0.4121,0.3876,0.4347,0.397,0.38,0.3631,0.3668,0.2971,0.912,0.8962,0.9185,0.939,0.9259,0.898,0.8887,0.8571,0.3989,0.3781,0.4215,0.3725,0.3612,0.3461,0.3423,0.2782,0.9092,0.8952,0.9176,0.9399,0.925,0.8971,0.8887,0.8571,0.4743,0.4536,0.4894,0.4517,0.446,0.4328,0.4385,0.3706,0.8273,0.8171,0.8571,0.8878,0.8766,0.8543,0.8561,0.8394,0.4743,0.4554,0.4969,0.4668,0.4536,0.4404,0.4536,0.3857)

w=matrix(w.vector,ncol=16,nrow=16,byrow=FALSE)

Затем создайте зарегистрированную матрицу измерений wm согласно уравнению 2 как

от

wm = w - rowMeans(w)

Мы можем разложить wm в матрицу '2FxP' o1 диагональная матрица PxP e и матрица "PxP" o2 используя сингулярное разложение значений.

svdwm <- svd(wm)

o1 <- svdwm$u
e <-  diag(svdwm$d)
o2 <- t(svdwm$v) ## dont forget the transpose!

Однако из-за шума мы обращаем внимание только на первые 3 столбца o1, первые 3 значения e и первые 3 ряда o2 от:

o1p <- svdwm$u[,1:3]
ep <-  diag(svdwm$d[1:3])
o2p <- t(svdwm$v)[1:3,] ## dont forget the transpose!

Теперь мы можем решить для нашего rhat а также shat в уравнении (14)

от

rhat <- o1p%*%ep^(1/2)
shat <- ep^(1/2) %*% o2p

Тем не менее, эти результаты не являются уникальными, и нам все еще нужно решить для R и S по уравнению (15)

используя метрические ограничения уравнения (16)

Теперь мне нужно найти Q. Я верю, что есть два возможных метода, но неясно, как их использовать.

Метод 1 включает решение для B, где B=Q%*%solve(Q) затем, используя разложение Холецкого, чтобы найти Q. Метод 1, по-видимому, является распространенным выбором в литературе, однако мало говорится о том, как на самом деле решить линейную систему. Очевидно, что B является симметричной матрицей "3х3" из 6 неизвестных. Однако, учитывая метрические ограничения (уравнения 16), я не знаю, как решить для 6 неизвестных данных 3 уравнения. Я забыл свойство симметричных матриц?

Метод II включает использование нелинейных методов для оценки Q и менее часто используется в структуре из литературы по движению.

Может ли кто-нибудь дать совет, как решить эту проблему? Спасибо заранее и дайте мне знать, если мне нужно быть более ясным в моем вопросе.

3

r opencv image-processing non-linear-regression structure-from-motion

Источник

user2138610 07 июн '16 в 23:30

1 ответ

Решение

Другие вопросы по тегам r opencv image-processing non-linear-regression structure-from-motion

user6796677 31 янв '17 в 14:50 2017-01-31 14:50 · Accepted Answer · 2017-01-31 14:50

$\hat{i}_{f}$ можно записать как ${a_if b_if c_if}$ ,

$\hat{j}_{f}$ можно записать как ${a_jf b_jf c_jf}$ ,

$QQ^T$ можно записать как $\begin{pmatrix} q_{11}&q_{12}&q_{13}\\ q_{12}&q_{22}&q_{23}\\ q_{13}&q_{23}&q_{33}\\ \end{pmatrix}$ ,

Итак, наши уравнения:

$\begin{pmatrix} a_{if}&b_{if}&c_{if} \end{pmatrix} \cdot \begin{pmatrix} q_{11}&q_{12}&q_{13}\\ q_{12}&q_{22}&q_{23}\\ q_{13}&q_{23}&q_{33}\\ \end{pmatrix} \cdot$ $\begin{pmatrix} a_{if}\\ b_{if}\\ c_{if}\\ \end{pmatrix} = 1$

$\begin{pmatrix} a_{jf}&b_{jf}&c_{jf} \end{pmatrix} \cdot \begin{pmatrix} q_{11}&q_{12}&q_{13}\\ q_{12}&q_{22}&q_{23}\\ q_{13}&q_{23}&q_{33}\\ \end{pmatrix} \cdot$ $\begin{pmatrix} a_{jf}\\ b_{jf}\\ c_{jf}\\ \end{pmatrix} = 1$

$\begin{pmatrix} a_{if}&b_{if}&c_{if} \end{pmatrix} \cdot \begin{pmatrix} q_{11}&q_{12}&q_{13}\\ q_{12}&q_{22}&q_{23}\\ q_{13}&q_{23}&q_{33}\\ \end{pmatrix} \cdot$ $\begin{pmatrix} a_{jf} \\ b_{jf} \\ c_{jf} \end{pmatrix} = 0$

Таким образом, первое уравнение может быть записано как:

$a_{if}\cdot a_{if}\cdot q_{11}+ a_{if}\cdot b_{if}\cdot q_{12}+ a_{if}\cdot c_{if}\cdot q_{13}$ $+ b_{if}\cdot a_{if}\cdot q_{12}+ b_{if}\cdot b_{if}\cdot q_{22}+ b_{if}\cdot c_{if}\cdot q_{23}$ $+ c_{if}\cdot a_{if}\cdot q_{13}+ c_{if}\cdot b_{if}\cdot q_{23}+ c_{if}\cdot c_{if}\cdot q_{33}=1$

$\Leftrightarrow a_{if}\cdot a_{if}\cdot q_{11}+ 2\cdot a_{if}\cdot b_{if}\cdot q_{12}+ 2\cdot a_{if}\cdot c_{if}\cdot q_{13}+$ $b_{if}\cdot b_{if}\cdot q_{22}+ 2\cdot b_{if}\cdot c_{if}\cdot q_{23}+ c_{if}\cdot c_{if}\cdot q_{33}=1$

что эквивалентно

$\begin{pmatrix} a_{if}a_{if}& 2a_{if}b_{if}& 2a_{if}c_{if}& b_{if}b_{if}& 2b_{if}c_{if}& c_{if}c_{if} \end{pmatrix}\cdot\\[35pt].$ $\begin{pmatrix} q_{11}\\ q_{12}\\ q_{13}\\ q_{22}\\ q_{23}\\ q_{33}\\ \end{pmatrix} = 1$

Для краткости мы сейчас определим:

$V_{x,y}\;:=\begin{pmatrix} a_{x}a_{y}& a_{x}b_{y}+a_{y}b_{x}& a_{x}c_{y}+a_{y}c_{x}& b_{x}b_{y}& b_{x}c_{y}+b_{y}c_{x}& c_{x}c_{y} \end{pmatrix}$ (Я знаю, что расстояния очень малы, но да, это вектор...)

Таким образом, для всех уравнений во всех разных кадрах f мы можем написать одно большое уравнение:

$\begin{pmatrix} V_{i1,i1}\\ V_{j1,j1}\\ V_{i1,j1}\\ V_{i2,i2}\\ V_{j2,j2}\\ V_{i2,j2}\\ \vdots\\ \end{pmatrix}\cdot$ $\begin{pmatrix} q_{11}\\ q_{12}\\ q_{13}\\ q_{22}\\ q_{23}\\ q_{33}\\ \end{pmatrix} = \begin{pmatrix} 1\\ 1\\ 0\\ 1\\ 1\\ 0\\ \vdots\\ \end{pmatrix}$

(извините за уродливые формулы...) Теперь вам просто нужно решить $QQ^T$ Матрица с использованием разложения Холецкого или что-то...