N-мерная регрессия ГП

Question

Я пытаюсь использовать GPflow для многомерной регрессии. Но меня смущают формы среднего и дисперсии. Например: 2-мерное пространство ввода X формы (20,20) должно быть предсказано. Мои тренировочные образцы имеют форму (8,2), что означает 8 тренировочных образцов в целом для двух измерений. Значения y имеют форму (8,1), что, конечно, означает одно значение истинности основания на комбинацию из 2 входных измерений. Если бы я теперь использовал model.predict_y(X), я ожидал бы получить среднее значение формы (20,20), но получить форму (20,1). То же самое касается дисперсии. Я думаю, что эта проблема связана с формой значений y, но я понятия не имею, как ее исправить.

bound = 3
num = 20
X = np.random.uniform(-bound, bound, (num,num))
print(X_sample.shape)  # (8,2)
print(Y_sample.shape)  # (8,1)
k = gpflow.kernels.RBF(input_dim=2)
m = gpflow.models.GPR(X_sample, Y_sample, kern=k)
m.likelihood.variance = sigma_n
m.compile()
gpflow.train.ScipyOptimizer().minimize(m)
mean, var = m.predict_y(X)
print(mean.shape)  # (20, 1)
print(var.shape)  # (20, 1)

Answer 1

Похоже, что вы можете быть запутаны между формой сетки входных позиций и формой числовых массивов: если вы хотите сделать прогноз на сетке 20 x 20 в двух измерениях, у вас есть 400 точек, каждая из которых имеет 2 значения, Итак, X (тот, который вы передаете m.predict_y()) должен иметь форму (400, 2). (Обратите внимание, что второе измерение должно иметь ту же форму, что и X_sample!) Для построения этого массива формы (400,2) вы можете использовать np.meshgrid (например, см. Какова цель сетки в Python / NumPy?).

m.predict_y(X) предсказывает только предельную дисперсию в каждой контрольной точке, поэтому mean а также var оба имеют форму (400,1) (той же длины, что и X). Конечно, вы можете изменить их до 20 х 20 значений в вашей сетке.

(Также возможно вычислить полную ковариацию, для скрытого f это реализуется как m.predict_f_full_cov, который для X формы (400,2) вернул бы матрицу 400x400. Это актуально, если вам нужны последовательные образцы от врача общей практики, но я подозреваю, что это выходит далеко за рамки этого вопроса.)

Answer 2

Я действительно делал ошибку, чтобы не сгладить массивы, которые взамен произвели ошибку. Спасибо за быстрый ответ STJ!

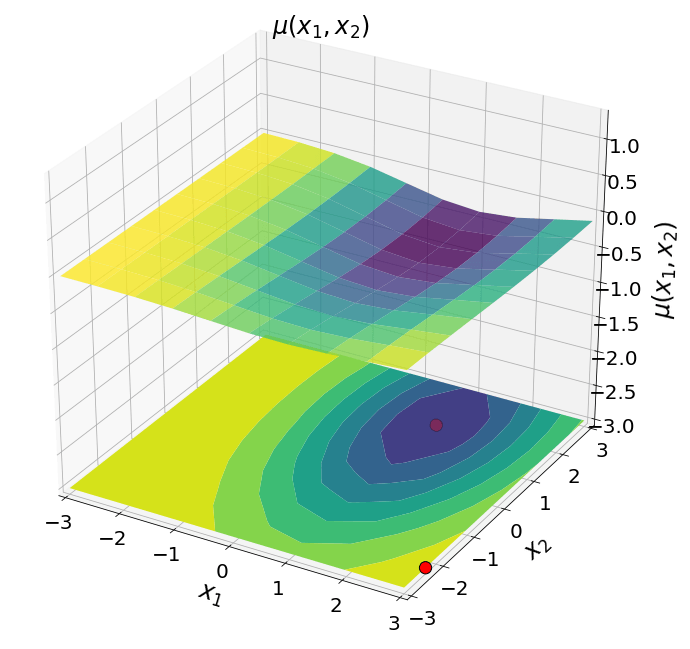
Вот пример рабочего кода:

# Generate data
bound = 3.
x1 = np.linspace(-bound, bound, num)
x2 = np.linspace(-bound, bound, num)
x1_mesh,x2_mesh = np.meshgrid(x1, x2)
X = np.dstack([x1_mesh, x2_mesh]).reshape(-1, 2)
z = f(x1_mesh, x2_mesh) # evaluation of the function on the grid

# Draw samples from feature vectors and function by a given index
size = 2
np.random.seed(1991)
index = np.random.choice(range(len(x1)), size=(size,X.ndim), replace=False)
samples = utils.sampleFeature([x1,x2], index)
X1_sample = samples[0]
X2_sample = samples[1]  
X_sample = np.column_stack((X1_sample, X2_sample))
Y_sample = utils.samplefromFunc(f=z, ind=index)



# Change noise parameter
sigma_n = 0.0
# Construct models with initial guess
k = gpflow.kernels.RBF(2,active_dims=[0,1], lengthscales=1.0,ARD=True)
m = gpflow.models.GPR(X_sample, Y_sample, kern=k)
m.likelihood.variance = sigma_n
m.compile()

#print(X.shape)
mean, var = m.predict_y(X)
mean_square = mean.reshape(x1_mesh.shape) # Shape: (num,num)
var_square = var.reshape(x1_mesh.shape) # Shape: (num,num)

# Plot mean
fig = plt.figure(figsize=(16, 12))
ax = plt.axes(projection='3d')
ax.plot_surface(x1_mesh, x2_mesh, mean_square, cmap=cm.viridis, linewidth=0.5, antialiased=True, alpha=0.8)
cbar = ax.contourf(x1_mesh, x2_mesh, mean_square, zdir='z', offset=offset, cmap=cm.viridis, antialiased=True)
ax.scatter3D(X1_sample, X2_sample, offset, marker='o',edgecolors='k', color='r', s=150)
fig.colorbar(cbar)


for t in ax.zaxis.get_major_ticks(): t.label.set_fontsize(fontsize_ticks)
ax.set_title("$\mu(x_1,x_2)$", fontsize=fontsize_title)
ax.set_xlabel("\n$x_1$", fontsize=fontsize_label)
ax.set_ylabel("\n$x_2$", fontsize=fontsize_label)
ax.set_zlabel('\n\n$\mu(x_1,x_2)$', fontsize=fontsize_label)
plt.xticks(fontsize=fontsize_ticks)
plt.yticks(fontsize=fontsize_ticks)
plt.xlim(left=-bound, right=bound)
plt.ylim(bottom=-bound, top=bound)
ax.set_zlim3d(offset,np.max(z))

что приводит к (красные точки - точки выборки, взятые из функции). Примечание: код не изменен, что так всегда:)