Тест на отсутствие изменений в Лимме

Question

Я ищу способ идентифицировать гены, которые значительно стабильны в любых условиях. Другими словами, противоположность стандартного анализа DE.

Стандарт DE расщепляет гены на две категории: значительно меняющиеся с одной стороны, все остальное, "остальные", с другой. "Остальное", однако, содержит как гены, которые на самом деле не меняются, так и гены, для которых уверенность в изменении не достаточна, чтобы назвать их дифференциальными.
Я хочу найти те, которые не меняются, или, другими словами, те, для которых я могу с уверенностью сказать, что в моих условиях нет изменений.

Я знаю, что это возможно в DEseq, предоставляя альтернативную нулевую гипотезу, но я должен интегрировать это как дополнительный шаг в чей-то конвейер, который уже использует лимму, и я хотел бы придерживаться этого. В идеале я хотел бы проверить и DE, и неизменяющиеся гены аналогичным образом, что-то концептуально похожее на изменение H0 в DEseq.

На данный момент код для тестирования на DE выглядит так:

# shaping data
comparison <- eBayes(lmFit(my_data, weights = my.weights^2))
results <- limma::topTable(my_data, sort.by = "t",  
                     coef = 1, number = Inf)

в качестве примера я хотел бы что-то вроде следующего, но все, что концептуально похоже будет делать.

comparison <- eBayes(lmFit(my_data, weights = my.weights^2), ALTERNATIVE_H0 = my_H0)

Я знаю, что Treat() позволяет задавать нулевую гипотезу с интервалом, предоставляя сгибное изменение, ссылаясь на руководство: "оно использует нулевую гипотезу с интервалом, где интервал равен [-lfc,lfc]".
Однако это все еще проверяет изменения от центрального интервала около 0, в то время как интервалы, которые я хотел бы проверить, являются [-inf,-lfc] + [lfc,inf].

Есть ли какой-то вариант, который я пропускаю?

Спасибо!

Answer 1

Вы можете попробовать использовать доверительный интервал logFC для выбора ваших генов, но я должен сказать, что это очень зависит от количества образцов, которые у вас есть, а также от того, насколько сильна биологическая дисперсия. Ниже я показываю пример, как это можно сделать:

сначала мы используем DESeq2 для создания примера набора данных, мы устанавливаем betaSD так, чтобы у нас была небольшая часть генов, которые должны показывать различия между условиями

library(DESeq2)
library(limma)
set.seed(100)
dds = makeExampleDESeqDataSet(n=2000,betaSD=1)
#pull out the data
DF = colData(dds)
# get out the true fold change
FC = mcols(dds)

Теперь мы можем запустить limma-voom на этом наборе данных,

V = voom(counts(dds),model.matrix(~condition,data=DF))
fit = lmFit(V,model.matrix(~condition,data=DF))
fit = eBayes(fit)
# get the results, in this case, we are interested in the 2nd coef
res = topTable(fit,coef=2,n=nrow(V),confint=TRUE)

Таким образом, есть возможность собрать 95% доверительный интервал кратного изменения в функции topTable. Мы делаем это и сравниваем с настоящим FC:

# fill in the true fold change
res$true_FC = FC[rownames(res),"trueBeta"]

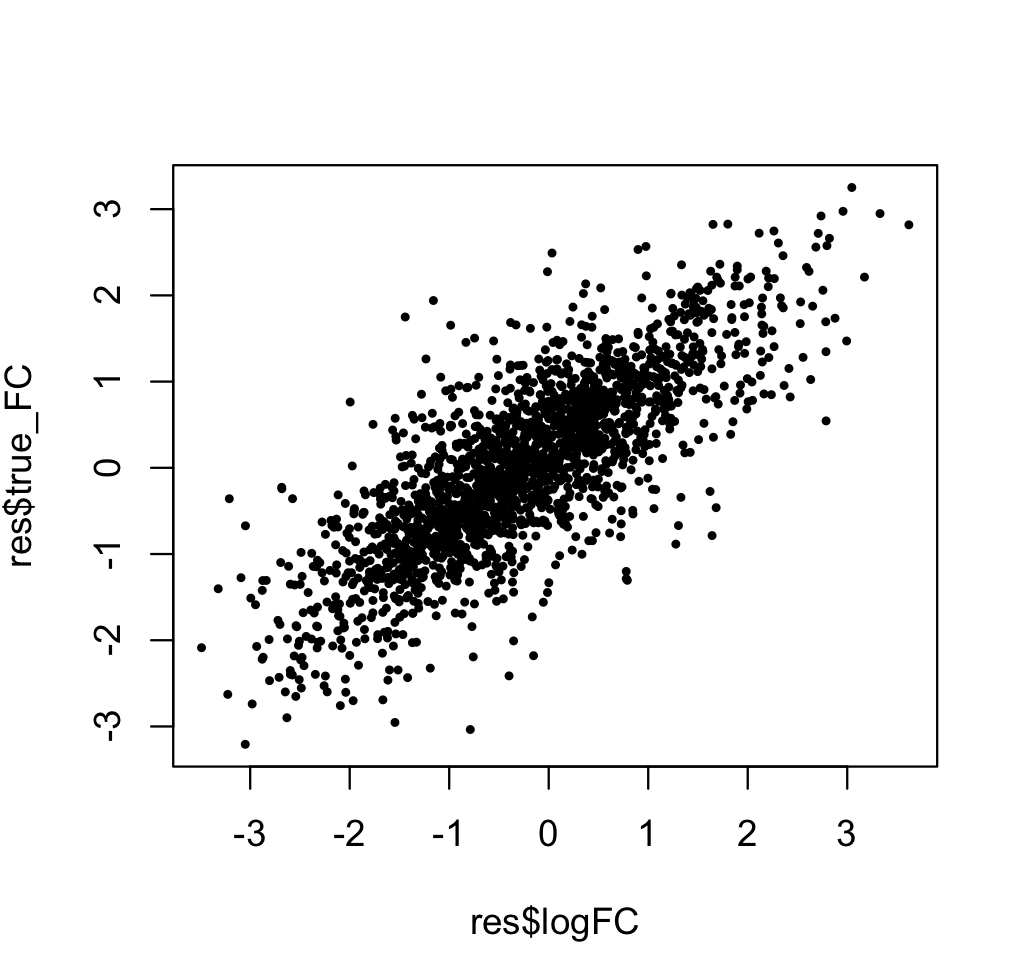
Мы можем посмотреть, чем отличаются оценочное и истинное:

plot(res$logFC,res$true_FC)

Допустим, мы хотим найти гены, где мы уверены, что кратность изменения < 1, мы можем:

tabResults = function(tab,fc_cutoff){
true_unchange = abs(tab$true_FC)<fc_cutoff
pred_unchange = tab$CI.L>(-fc_cutoff) & res$CI.R <fc_cutoff
list(
X = table(pred_unchange,true_unchange),
expression_distr = aggregate(
tab$AveExpr ~ pred_unchange+true_unchange,data=tab,mean
))
}

tabResults(res,1)$X

             true_unchange
pred_unchange FALSE TRUE
        FALSE   617 1249
        TRUE      7  127

Приведенные выше результаты говорят нам, что если мы установим ограничение для генов, 95% -ная достоверность которых находится в пределах +/- 1 FC, мы получим 134 совпадения, причем 7 будет ложным (с фактическим кратным изменением> 1).

Причина, по которой мы упускаем некоторые истинные неизменяющиеся гены, заключается в том, что они экспрессируются немного ниже, в то время как большая часть того, что мы правильно предсказали как неизменные, имеет высокую экспрессию:

tabResults(res,1)$expression_distr

  pred_unchange true_unchange tab$AveExpr
1         FALSE         FALSE    7.102364
2          TRUE         FALSE    8.737670
3         FALSE          TRUE    6.867615
4          TRUE          TRUE   10.042866

Мы можем снизить FC, но в итоге мы получим меньше генов:

tabResults(res,0.7)

             true_unchange
pred_unchange FALSE TRUE
        FALSE   964 1016
        TRUE      1   19

Доверительный интервал во многом зависит от количества имеющихся у вас образцов. Таким образом, пороговое значение 1 для одного набора данных будет означать что-то другое для другого.

Итак, я бы сказал, что если у вас есть набор данных, вы можете сначала запустить DESeq2 для этого набора данных, получить отношение средней дисперсии и смоделировать данные, как это сделал я, чтобы более или менее догадаться, какое отсечение изменения кратности будет в порядке, сколько вы можете получить и принять решение оттуда.