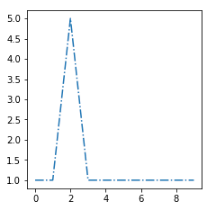
Метрика расстояния временного ряда
Для кластеризации набора временных рядов я ищу умную метрику расстояния. Я пробовал некоторые хорошо известные показатели, но никто не подходит к моему случаю.
пример: предположим, что мой кластерный алгоритм извлекает эти три центроида [s1, s2, s3]: 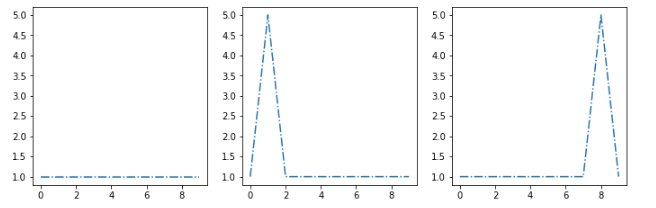
Я хочу поместить этот новый пример [sx] в наиболее похожий кластер:
Наиболее похожими центроидами являются вторые, поэтому мне нужно найти функцию расстояния d, которая дает мне d(sx, s2) < d(sx, s1) а также d(sx, s2) < d(sx, s3)
редактировать
Вот результаты с метриками [косинус, евклидов, минковский, динамическое искажение типа]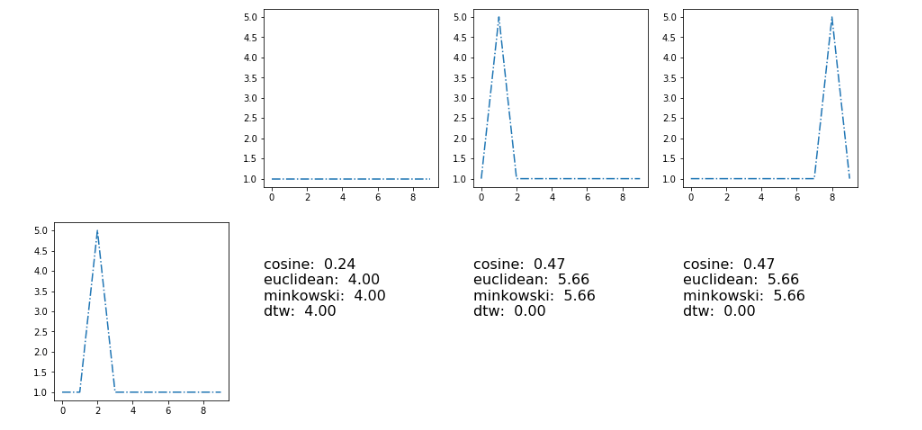 ] 3
] 3
редактировать 2
Пользователь Pietro P предложил применить расстояния к накопленной версии временного ряда. Решение работает, вот графики и метрики: 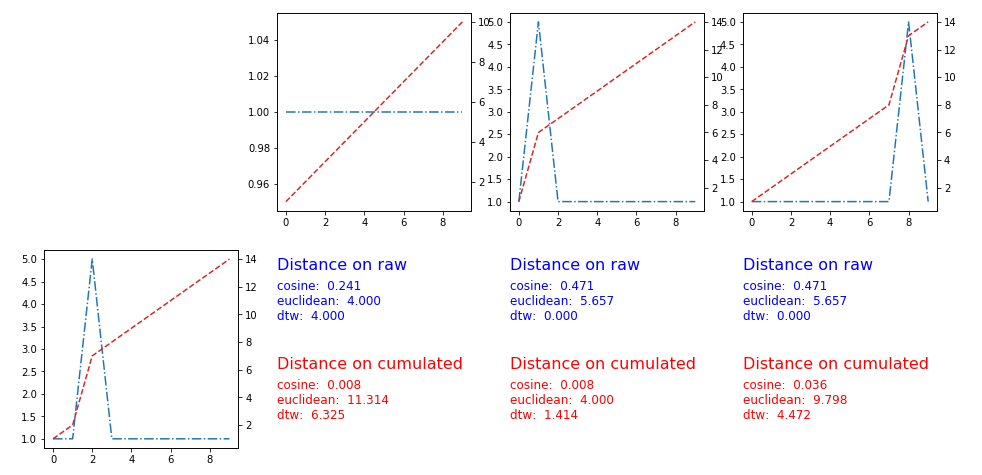
2 ответа
Хороший вопрос! использование любого стандартного расстояния R^n (евклидово, манхэттенское или в общем случае минковского) по этим временным рядам не может достичь желаемого результата, поскольку эти метрики не зависят от перестановок координаты R^n (в то время как время строго упорядочено и оно это феномен, который вы хотите запечатлеть).
Простой трюк, который может сделать то, что вы просите, - использовать накопленную версию временного ряда (сумма значений во времени с увеличением времени), а затем применить стандартную метрику. Используя метрику Манхэттена, вы получите как расстояние между двумя временными рядами площадь между их накопленными версиями.
Другой подход может заключаться в использовании DTW, который представляет собой алгоритм для вычисления сходства между двумя временными последовательностями. Полное раскрытие; Для этой цели я написал пакет Python под названиемtrendypy, вы можете скачать через pip (pip install trendypy). Вот демонстрация того, как использовать пакет. Вы просто в основном вычисляете общее минимальное расстояние для различных комбинаций, чтобы установить центры кластера.
Ответ Пьетро П. - это просто частный случай применения свертки к вашему временному ряду.
Если бы я дал ядро:
[1,1,...,1,1,1,0,0,0,0,...0,0]
Получил бы кумулятивный ряд.
Добавление свертки работает, потому что вы даете каждой точке данных информацию о ее соседях - теперь она зависит от порядка.
Было бы интересно попробовать с гуасовой сверткой или другими ядрами.
Как насчет использования стандартного коэффициента корреляции Пирсона? затем вы можете назначить новую точку кластеру с наибольшим коэффициентом.
correlation = scipy.stats.pearsonr(<new time series>, <centroid>)