Как расположить кольцо кругов с максимальным радиусом кольца

Question

Я пытаюсь создать кольцо из кругов, аля:

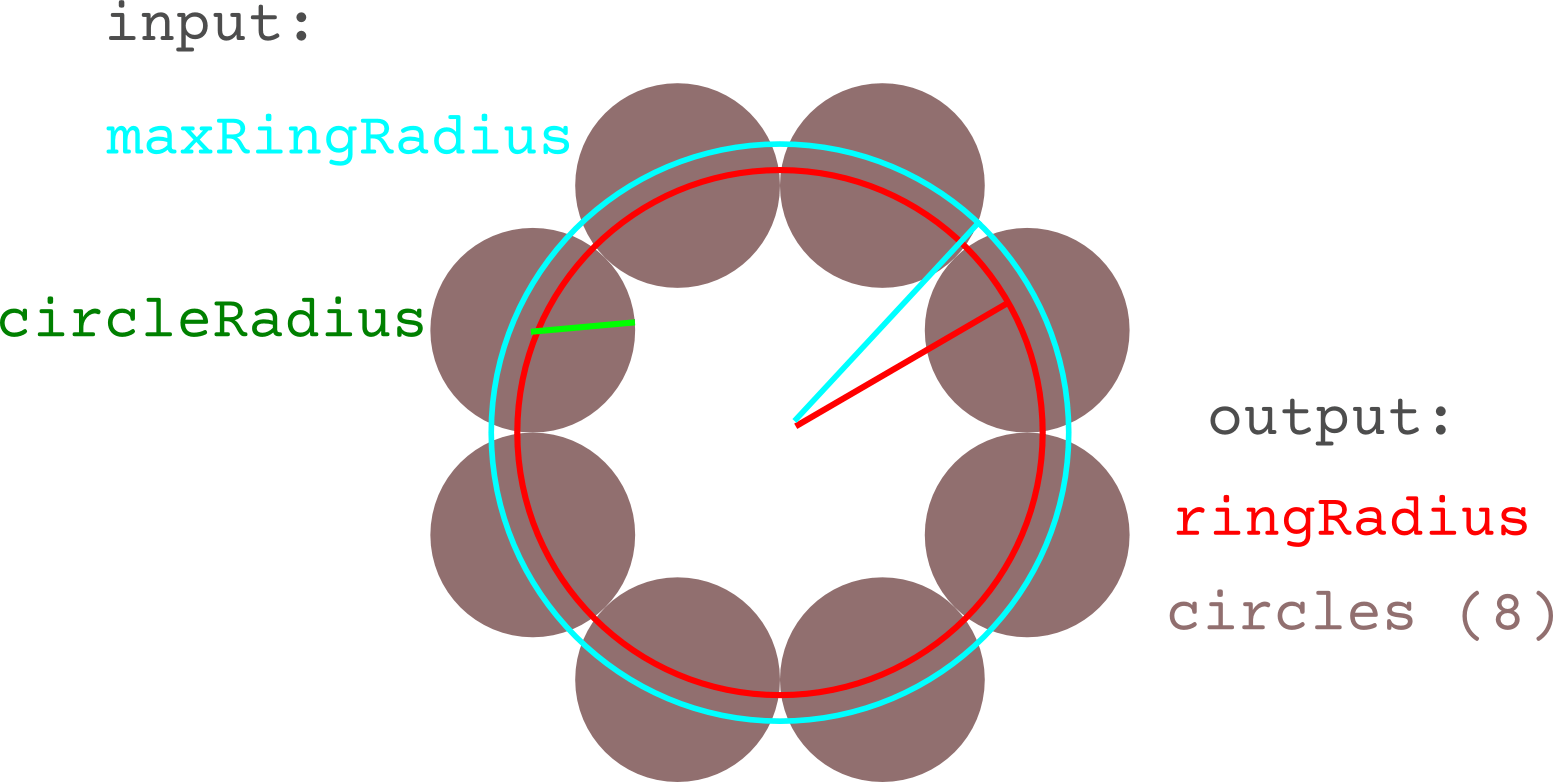
Круги имеют заданный радиус, circleRadius, Кольцо имеет максимальный радиус, maxRingRadius, Количество кружков может быть любым целым числом, circles, который должен быть рассчитан вместе с фактическим радиусом кольца, ringRadius, Круги, когда их центры расположены ringRadius единицы от центра кольца, должны быть точно соприкасающимися, как на схеме.

Учитывая circleRadius и maxRingRadius как найти ближайший (или следующий наименьший) ringRadius который будет соответствовать целому числу circles, а затем позиционировать эти круги?

    static Vector3[] RingOfCircles(float maxRingRadius, float circleRadius) {
        //int circles = ...; // calculate this?
        //float ringRadius = ...; // calculate this?

        //Edit: Solution. These three lines are adapted from InBetween's GetNextSmallerRingRadius function but Unity3d-ized and without validation
        int circles = Mathf.RoundToInt(Mathf.PI / Mathf.Asin(circleRadius / maxRingRadius)); 
        float centralAngle = 2 * Mathf.PI / (numberOfCircles - 1);
        float ringRadius = circleRadius / Mathf.Sin(centralAngle / 2);

        // create ring of center points
        float radsPerCircle = (Mathf.PI * 2) / circles;
        Vector3[] centerPoints = new Vector3[circles];
        for (int i=0; i < circles; i++) {
            float angle = i * radsPerCircle;
            centerPoints[i] = new Vector3(
                Mathf.Sin(angle) * ringRadius, 
                Mathf.Cos(angle) * ringRadius, 
                0);
        }

        return centerPoints;
    }
`

Замечания: maxRingRadius с таким же успехом может быть minRingRadius или же approximateRingRadius для моих целей. Но ringRadius должен определить следующее ближайшее "кольцо", которое может содержать целое число кругов.

---

Решено: Визуальное подтверждение решения

Answer 1

Если я правильно понял ваш вопрос, это должно сделать это:

 public static double GetNextSmallerRingRadius(double startingRingRadius, double circleRadius)
 {
     Debug.Assert(startingRingRadius >= 0);
     Debug.Assert(circleRadius > 0);

     int currentNumberOfCircles = GetCurrentNumberOfCircles(startingRingRadius, circleRadius);

     //Let's get trivial cases out of the way
     if (currentNumberOfCircles == 1)
         throw new ArgumentException();
     if (currentNumberOfCircles == 2)
         return 0; //trivial solution for 1 circle.
     if (currentNumberOfCircles == 3)
         return circleRadius; //trivial solution for 2 circles.

     double centralAngle = 2 * Math.PI / (currentNumberOfCircles - 1);
     return circleRadius / Math.Sin(centralAngle / 2);
 }

 public static double GetNextLargerRingRadius(double startingRingRadius, double circleRadius)
 {
     Debug.Assert(startingRingRadius >= 0);
     Debug.Assert(circleRadius > 0);

     int currentNumberOfCircles = GetCurrentNumberOfCircles(startingRingRadius, circleRadius);

     //Let's get trivial cases out of the way
     if (currentNumberOfCircles == 1)
         return circleRadius; //trivial solution for 2 circles.

     double centralAngle = 2 * Math.PI / (currentNumberOfCircles + 1);
     return circleRadius / Math.Sin(centralAngle / 2);
 }

 private static int GetCurrentNumberOfCircles(double startingRingRadius, double circleRadius)
 {
     if (startingRingRadius == 0)
     {
         return 1;
     }
     else
     {
         return (int)Math.Round(Math.PI / Math.Asin(circleRadius / startingRingRadius), 0); //There would need to be some logic to make sure input values are correct.
     }
 }

Чтобы подтвердить ввод (определенные радиусы представляют собой правильное решение), вы можете сравнить округленное и не округленное numberOfcircles и убедитесь, что разница находится внутри заданного допуска. Помните, с double Вы не можете проверить на равенство, так как всегда будет ошибка представления.

ОБНОВЛЕНИЕ Ой, я не видел, что вы также спрашивали о размещении кругов. Как только вы знаете радиус кольца и центральный угол, это довольно просто.