Как я могу использовать numpy.correlate для автокорреляции?

Question

Мне нужно сделать автокорреляцию набора чисел, который, как я понимаю, является просто корреляцией набора с самим собой.

Я попробовал это, используя функцию корреляции numpy, но я не верю результату, так как он почти всегда дает вектор, где первое число не самое большое, как и должно быть.

Итак, этот вопрос на самом деле два вопроса:

1. Что именно numpy.correlate делать?
2. Как я могу использовать это (или что-то еще), чтобы сделать автокорреляцию?

Answer 1

Чтобы ответить на ваш первый вопрос, numpy.correlate(a, v, mode) выполняет свертку a с обратной v и выдача результатов, ограниченных указанным режимом. Определение свертки, C (t) = ∑ _{-∞ a i v t + i, где -∞}

• "полный" режим возвращает результаты для каждого t где оба a а также v иметь некоторое совпадение.
• "тот же" режим возвращает результат такой же длины, что и самый короткий вектор (a или же v).
• "действительный" режим возвращает результаты только тогда, когда a а также v полностью перекрывают друг друга. Документация для numpy.convolve дает более подробную информацию о режимах.

На ваш второй вопрос, я думаю numpy.correlate дает вам автокорреляцию, просто дает вам немного больше. Автокорреляция используется для определения того, насколько похож сигнал или функция на себя при определенной разнице во времени. При разнице во времени 0 автокорреляция должна быть наибольшей, поскольку сигнал идентичен самому себе, поэтому вы ожидали, что первый элемент в массиве результатов автокорреляции будет наибольшим. Однако корреляция не начинается с разницы во времени 0. Она начинается с отрицательной разницы во времени, закрывается до 0 и затем становится положительной. То есть вы ожидали

автокорреляция (а) = ∑ _{-∞ a i v t + i, где 0 <= t <∞}

Но то, что вы получили, было:

автокорреляция (a) = ∑ _{-∞ a i v t + i, где -∞}

Что вам нужно сделать, это взять вторую половину результата корреляции, и это должна быть автокорреляция, которую вы ищете. Простая функция Python для этого будет:

def autocorr(x):
    result = numpy.correlate(x, x, mode='full')
    return result[result.size/2:]

Вам, конечно, понадобится проверка ошибок, чтобы убедиться, что x на самом деле 1-й массив. Кроме того, это объяснение, вероятно, не является наиболее математически строгим. Я разбрасывал бесконечности, потому что определение свертки использует их, но это не обязательно относится к автокорреляции. Таким образом, теоретическая часть этого объяснения может быть немного сомнительной, но, надеюсь, практические результаты окажутся полезными. Эти страницы, посвященные автокорреляции, очень полезны и могут дать вам гораздо лучшую теоретическую подготовку, если вы не возражаете разобраться с обозначениями и сложными концепциями.

Answer 2

Автокорреляция поставляется в двух версиях: статистическая и свертка. Они оба делают то же самое, за исключением небольшой детали: первый нормализуется, чтобы быть на интервале [-1,1]. Вот пример того, как вы делаете статистический:

def acf(x, length=20):
    return numpy.array([1]+[numpy.corrcoef(x[:-i], x[i:]) \
        for i in range(1, length)])

Answer 3

Я думаю, что есть две вещи, которые добавляют путаницу к этой теме:

1. статистическое определение и обработка сигналов: как уже указывали другие, в статистике мы нормализуем автокорреляцию в [-1,1].
2. частичное по сравнению с неполным средним / дисперсией: когда временные ряды сдвигаются с задержкой>0, их размер перекрытия всегда будет <исходной длины. Используем ли мы среднее и стандартное отклонение оригинала (не частичное), или всегда вычисляем новое среднее значение, и стандартное отклонение, используя постоянно меняющееся перекрытие (частичное), имеет значение. (Возможно, для этого есть формальный термин, но сейчас я буду использовать "частичный").

Я создал 5 функций, которые вычисляют автокорреляцию 1d массива, с частичными и не частичными различиями. Некоторые используют формулу из статистики, некоторые используют коррелят в смысле обработки сигнала, что также может быть сделано через FFT. Но все результаты являются автокорреляциями в определении статистики, поэтому они иллюстрируют, как они связаны друг с другом. Код ниже:

import numpy
import matplotlib.pyplot as plt

def autocorr1(x,lags):
    '''numpy.corrcoef, partial'''

    corr=[1. if l==0 else numpy.corrcoef(x[l:],x[:-l])[0][1] for l in lags]
    return numpy.array(corr)

def autocorr2(x,lags):
    '''manualy compute, non partial'''

    mean=numpy.mean(x)
    var=numpy.var(x)
    xp=x-mean
    corr=[1. if l==0 else numpy.sum(xp[l:]*xp[:-l])/len(x)/var for l in lags]

    return numpy.array(corr)

def autocorr3(x,lags):
    '''fft, pad 0s, non partial'''

    n=len(x)
    # pad 0s to 2n-1
    ext_size=2*n-1
    # nearest power of 2
    fsize=2**numpy.ceil(numpy.log2(ext_size)).astype('int')

    xp=x-numpy.mean(x)
    var=numpy.var(x)

    # do fft and ifft
    cf=numpy.fft.fft(xp,fsize)
    sf=cf.conjugate()*cf
    corr=numpy.fft.ifft(sf).real
    corr=corr/var/n

    return corr[:len(lags)]

def autocorr4(x,lags):
    '''fft, don't pad 0s, non partial'''
    mean=x.mean()
    var=numpy.var(x)
    xp=x-mean

    cf=numpy.fft.fft(xp)
    sf=cf.conjugate()*cf
    corr=numpy.fft.ifft(sf).real/var/len(x)

    return corr[:len(lags)]

def autocorr5(x,lags):
    '''numpy.correlate, non partial'''
    mean=x.mean()
    var=numpy.var(x)
    xp=x-mean
    corr=numpy.correlate(xp,xp,'full')[len(x)-1:]/var/len(x)

    return corr[:len(lags)]


if __name__=='__main__':

    y=[28,28,26,19,16,24,26,24,24,29,29,27,31,26,38,23,13,14,28,19,19,\
            17,22,2,4,5,7,8,14,14,23]
    y=numpy.array(y).astype('float')

    lags=range(15)
    fig,ax=plt.subplots()

    for funcii, labelii in zip([autocorr1, autocorr2, autocorr3, autocorr4,
        autocorr5], ['np.corrcoef, partial', 'manual, non-partial',
            'fft, pad 0s, non-partial', 'fft, no padding, non-partial',
            'np.correlate, non-partial']):

        cii=funcii(y,lags)
        print(labelii)
        print(cii)
        ax.plot(lags,cii,label=labelii)

    ax.set_xlabel('lag')
    ax.set_ylabel('correlation coefficient')
    ax.legend()
    plt.show()

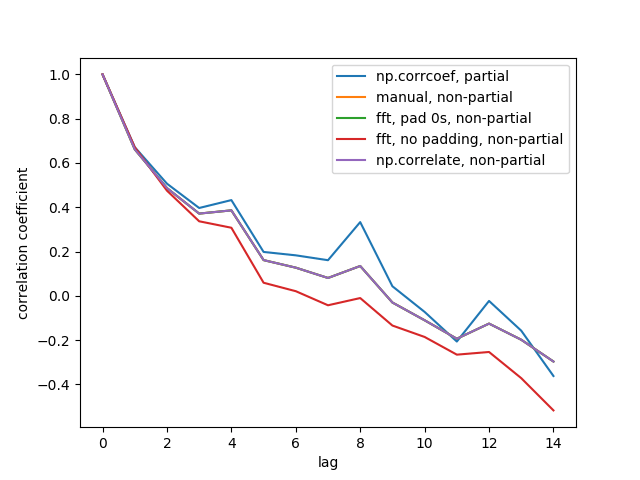
Вот выходной показатель:

Мы не видим все 5 линий, потому что 3 из них перекрываются (на фиолетовом). Перекрытия - это все неполные автокорреляции. Это потому, что вычисления из методов обработки сигналов (np.correlate, FFT) не вычислять различное среднее значение / стандартное отклонение для каждого перекрытия.

Также обратите внимание, что fft, no padding, non-partial (красная линия) результат отличается, потому что он не заполнял временные ряды нулями перед выполнением FFT, поэтому это круговое FFT. Я не могу подробно объяснить, почему, это то, что я узнал из других источников.

Answer 4

С использованием numpy.corrcoef функция вместо numpy.correlate Рассчитать статистическую корреляцию для лага t:

def autocorr(x, t=1):
    return numpy.corrcoef(numpy.array([x[0:len(x)-t], x[t:len(x)]]))

Answer 5

Поскольку я столкнулся с той же проблемой, я хотел бы поделиться с вами несколькими строками кода. На самом деле на данный момент есть несколько довольно похожих сообщений об автокорреляции в stackru. Если вы определяете автокорреляцию как a(x, L) = sum(k=0,N-L-1)((xk-xbar)*(x(k+L)-xbar))/sum(k=0,N-1)((xk-xbar)**2) [это определение, данное в IDL-функции a_correlate, и оно согласуется с тем, что я вижу в ответе 2 на вопрос № 12269834], тогда следующее, по-видимому, дает правильные результаты:

import numpy as np
import matplotlib.pyplot as plt

# generate some data
x = np.arange(0.,6.12,0.01)
y = np.sin(x)
# y = np.random.uniform(size=300)
yunbiased = y-np.mean(y)
ynorm = np.sum(yunbiased**2)
acor = np.correlate(yunbiased, yunbiased, "same")/ynorm
# use only second half
acor = acor[len(acor)/2:]

plt.plot(acor)
plt.show()

Как вы видите, я проверил это с помощью кривой sin и равномерного случайного распределения, и оба результата выглядят так, как я ожидал. Обратите внимание, что я использовал mode="same" вместо mode="full" как и другие.

Answer 6

Ваш вопрос 1 уже широко обсуждался в нескольких отличных ответах здесь.

Я подумал поделиться с вами несколькими строками кода, которые позволят вам вычислить автокорреляцию сигнала, основываясь только на математических свойствах автокорреляции. То есть автокорреляция может быть вычислена следующим образом:

1. вычесть среднее значение из сигнала и получить несмещенный сигнал

2. вычислить преобразование Фурье несмещенного сигнала

3. вычислить спектральную плотность мощности сигнала, взяв квадратную норму каждого значения преобразования Фурье несмещенного сигнала

4. вычислить обратное преобразование Фурье спектральной плотности мощности

5. нормализуем обратное преобразование Фурье спектральной плотности мощности по сумме квадратов несмещенного сигнала и берут только половину результирующего вектора

Код для этого следующий:

def autocorrelation (x) :
    """
    Compute the autocorrelation of the signal, based on the properties of the
    power spectral density of the signal.
    """
    xp = x-np.mean(x)
    f = np.fft.fft(xp)
    p = np.array([np.real(v)**2+np.imag(v)**2 for v in f])
    pi = np.fft.ifft(p)
    return np.real(pi)[:x.size/2]/np.sum(xp**2)

Answer 7

Альтернатива numpy.correlate доступна в statsmodels.tsa.stattools.acf (). Это дает непрерывно убывающую функцию автокорреляции, подобную описанной OP. Реализовать его довольно просто:

from statsmodels.tsa import stattools
# x = 1-D array
# Yield normalized autocorrelation function of number lags
autocorr = stattools.acf( x )

# Get autocorrelation coefficient at lag = 1
autocorr_coeff = autocorr[1]

Поведение по умолчанию - остановка на 40 nlags, но это можно настроить с помощью nlag=вариант для вашего конкретного приложения. Внизу страницы есть ссылка на статистику функции.

Answer 8

Я вычислительный биолог, и когда мне пришлось вычислять авто / взаимные корреляции между парами временных рядов случайных процессов, я понял, что np.correlate не выполняет нужную мне работу.

Действительно, в np.correlate, по-видимому, отсутствует усреднение по всем возможным парам временных точек на расстоянии \ tau.

Вот как я определил функцию, которая делает то, что мне нужно:

def autocross(x, y):
    c = np.correlate(x, y, "same")
    v = [c[i]/( len(x)-abs( i - (len(x)/2)  ) ) for i in range(len(c))]
    return v

Мне кажется, что ни один из предыдущих ответов не охватывает этот случай авто / взаимной корреляции: надеюсь, что этот ответ может быть полезен для кого-то, работающего над случайными процессами, такими как я.

Answer 9

Использование преобразования Фурье и теорема о свертке

Сложность времени N*log(N)

def autocorr1(x):
    r2=np.fft.ifft(np.abs(np.fft.fft(x))**2).real
    return r2[:len(x)//2]

Вот нормализованная и непредвзятая версия, это также N*log(N)

def autocorr2(x):
    r2=np.fft.ifft(np.abs(np.fft.fft(x))**2).real
    c=(r2/x.shape-np.mean(x)**2)/np.std(x)**2
    return c[:len(x)//2]

Метод, предоставленный А. Леви, работает, но я проверил его на своем ПК, его сложность во времени, кажется, N*N

def autocorr(x):
    result = numpy.correlate(x, x, mode='full')
    return result[result.size/2:]

Answer 10

Простое решение без панд:

import numpy as np

def auto_corrcoef(x):
   return np.corrcoef(x[1:-1], x[2:])[0,1]

Answer 11

Я использую talib.CORREL для такой автокорреляции, я подозреваю, что вы могли бы сделать то же самое с другими пакетами:

def autocorrelate(x, period):

    # x is a deep indicator array 
    # period of sample and slices of comparison

    # oldest data (period of input array) may be nan; remove it
    x = x[-np.count_nonzero(~np.isnan(x)):]
    # subtract mean to normalize indicator
    x -= np.mean(x)
    # isolate the recent sample to be autocorrelated
    sample = x[-period:]
    # create slices of indicator data
    correls = []
    for n in range((len(x)-1), period, -1):
        alpha = period + n
        slices = (x[-alpha:])[:period]
        # compare each slice to the recent sample
        correls.append(ta.CORREL(slices, sample, period)[-1])
    # fill in zeros for sample overlap period of recent correlations    
    for n in range(period,0,-1):
        correls.append(0)
    # oldest data (autocorrelation period) will be nan; remove it
    correls = np.array(correls[-np.count_nonzero(~np.isnan(correls)):])      

    return correls

# CORRELATION OF BEST FIT
# the highest value correlation    
max_value = np.max(correls)
# index of the best correlation
max_index = np.argmax(correls)

Answer 12

Чтобы реализовать функцию a_correlate IDL с помощью numpy, вам нужно запуститьnp.correlateсmode="full"и добавитьn-1кlagмножество.

      def a_correlate(y, lag):
    y = np.asarray(y)
    lag = np.asarray(lag)
    n = len(y)
    yunbiased = y - np.mean(y)
    ynorm = np.sum(yunbiased**2)
    r = np.correlate(yunbiased, yunbiased, "full") / ynorm
    return r[lag + (n - 1)]

Пример (на основе примера на странице документации IDL, указанной выше):

      # Define an n-element sample population:
X = np.array([3.73, 3.67, 3.77, 3.83, 4.67, 5.87, 6.70, 6.97, 6.40, 5.57])
# Compute the autocorrelation of X for LAG = -3, 0, 1, 3, 4, 8:
lag = [-3, 0, 1, 3, 4, 8]
result = a_correlate(X, lag)
print(result)
# prints: [ 0.01461851  1.          0.81087925  0.01461851 -0.32527914 -0.15168379]

Answer 13

Построить статистическую автокорреляцию с данными PANDAS DataTime Серия возвратов:

import matplotlib.pyplot as plt

def plot_autocorr(returns, lags):
    autocorrelation = []
    for lag in range(lags+1):
        corr_lag = returns.corr(returns.shift(-lag)) 
        autocorrelation.append(corr_lag)
    plt.plot(range(lags+1), autocorrelation, '--o')
    plt.xticks(range(lags+1))
    return np.array(autocorrelation)

Answer 14

Я думаю, что реальный ответ на вопрос OP кратко содержится в этом отрывке из документации Numpy.correlate:

mode : {'valid', 'same', 'full'}, optional
    Refer to the `convolve` docstring.  Note that the default
    is `valid`, unlike `convolve`, which uses `full`.

Это подразумевает, что при использовании без определения 'mode' функция Numpy.correlate будет возвращать скаляр, если ему дан один и тот же вектор для двух входных аргументов (т. Е. - когда используется для выполнения автокорреляции).