Есть ли какая-нибудь функция автокорреляции с унифицированным выводом?
Я последовал совету определения функции автокорреляции в другом посте:
def autocorr(x):
result = np.correlate(x, x, mode = 'full')
maxcorr = np.argmax(result)
#print 'maximum = ', result[maxcorr]
result = result / result[maxcorr] # <=== normalization
return result[result.size/2:]
однако максимальное значение не было "1.0". поэтому я ввел строку с тегом "<=== нормализация"
Я попробовал эту функцию с набором данных из главы 2 "Анализ временных рядов" (Бокс - Дженкинс). Я ожидал получить такой результат, как рис. 2,7 в этой книге. Однако я получил следующее:
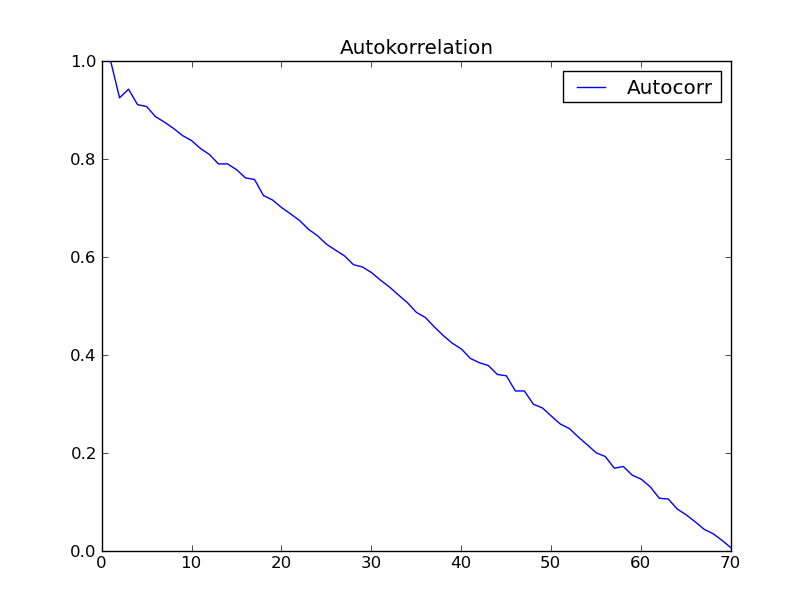
У кого-нибудь есть объяснение этому странному непредвиденному поведению автокорреляции?
Дополнение (2012-09-07):
Я попал в Python - программирование и сделал следующее:
from ClimateUtilities import *
import phys
#
# the above imports are from R.T.Pierrehumbert's book "principles of planetary
# climate"
# and the homepage of that book at "cambridge University press" ... they mostly
# define the
# class "Curve()" used in the below section which is not necessary in order to solve
# my
# numpy-problem ... :)
#
import numpy as np;
import scipy.spatial.distance;
# functions to be defined ... :
#
#
def autocorr(x):
result = np.correlate(x, x, mode = 'full')
maxcorr = np.argmax(result)
# print 'maximum = ', result[maxcorr]
result = result / result[maxcorr]
#
return result[result.size/2:]
##
# second try ... "Box and Jenkins" chapter 2.1 Autocorrelation Properties
# of stationary models
##
# from table 2.1 I get:
s1 = np.array([47,64,23,71,38,64,55,41,59,48,71,35,57,40,58,44,\
80,55,37,74,51,57,50,60,45,57,50,45,25,59,50,71,56,74,50,58,45,\
54,36,54,48,55,45,57,50,62,44,64,43,52,38,59,\
55,41,53,49,34,35,54,45,68,38,50,\
60,39,59,40,57,54,23],dtype=float);
# alternatively in order to test:
s2 = np.array([47,64,23,71,38,64,55,41,59,48,71])
##################################################################################3
# according to BJ, ch.2
###################################################################################3
print '*************************************************'
global s1short, meanshort, stdShort, s1dev, s1shX, s1shXk
s1short = s1
#s1short = s2 # for testing take s2
meanshort = s1short.mean()
stdShort = s1short.std()
s1dev = s1short - meanshort
#print 's1short = \n', s1short, '\nmeanshort = ', meanshort, '\ns1deviation = \n',\
# s1dev, \
# '\nstdShort = ', stdShort
s1sh_len = s1short.size
s1shX = np.arange(1,s1sh_len + 1)
#print 'Len = ', s1sh_len, '\nx-value = ', s1shX
##########################################################
# c0 to be computed ...
##########################################################
sumY = 0
kk = 1
for ii in s1shX:
#print 'ii-1 = ',ii-1,
if ii > s1sh_len:
break
sumY += s1dev[ii-1]*s1dev[ii-1]
#print 'sumY = ',sumY, 's1dev**2 = ', s1dev[ii-1]*s1dev[ii-1]
c0 = sumY / s1sh_len
print 'c0 = ', c0
##########################################################
# now compute autocorrelation
##########################################################
auCorr = []
s1shXk = s1shX
lenS1 = s1sh_len
nn = 1 # factor by which lenS1 should be divided in order
# to reduce computation length ... 1, 2, 3, 4
# should not exceed 4
#print 's1shX = ',s1shX
for kk in s1shXk:
sumY = 0
for ii in s1shX:
#print 'ii-1 = ',ii-1, ' kk = ', kk, 'kk+ii-1 = ', kk+ii-1
if ii >= s1sh_len or ii + kk - 1>=s1sh_len/nn:
break
sumY += s1dev[ii-1]*s1dev[ii+kk-1]
#print sumY, s1dev[ii-1], '*', s1dev[ii+kk-1]
auCorrElement = sumY / s1sh_len
auCorrElement = auCorrElement / c0
#print 'sum = ', sumY, ' element = ', auCorrElement
auCorr.append(auCorrElement)
#print '', auCorr
#
#manipulate s1shX
#
s1shX = s1shXk[:lenS1-kk]
#print 's1shX = ',s1shX
#print 'AutoCorr = \n', auCorr
#########################################################
#
# first 15 of above Values are consistent with
# Box-Jenkins "Time Series Analysis", p.34 Table 2.2
#
#########################################################
s1sh_sdt = s1dev.std() # Standardabweichung short
#print '\ns1sh_std = ', s1sh_sdt
print '#########################################'
# "Curve()" is a class from RTP ClimateUtilities.py
c2 = Curve()
s1shXfloat = np.ndarray(shape=(1,lenS1),dtype=float)
s1shXfloat = s1shXk # to make floating point from integer
# might be not necessary
#print 'test plotting ... ', s1shXk, s1shXfloat
c2.addCurve(s1shXfloat)
c2.addCurve(auCorr, '', 'Autocorr')
c2.PlotTitle = 'Autokorrelation'
w2 = plot(c2)
##########################################################
#
# now try function "autocorr(arr)" and plot it
#
##########################################################
auCorr = autocorr(s1short)
c3 = Curve()
c3.addCurve( s1shXfloat )
c3.addCurve( auCorr, '', 'Autocorr' )
c3.PlotTitle = 'Autocorr with "autocorr"'
w3 = plot(c3)
#
# well that should it be!
#
2 ответа
Итак, ваша проблема с вашей первоначальной попыткой состоит в том, что вы не вычли среднее значение из вашего сигнала. Следующий код должен работать:
timeseries = (your data here)
mean = np.mean(timeseries)
timeseries -= np.mean(timeseries)
autocorr_f = np.correlate(timeseries, timeseries, mode='full')
temp = autocorr_f[autocorr_f.size/2:]/autocorr_f[autocorr_f.size/2]
iact.append(sum(autocorr_f[autocorr_f.size/2:]/autocorr_f[autocorr_f.size/2]))
В моем примере temp интересующая вас переменная; это прямая интегрированная функция автокорреляции. Если вы хотите интегрированное время автокорреляции, вы заинтересованы в iact,
Я не уверен, в чем проблема.
Автокорреляция вектора x должно быть 1 с задержкой 0, так как это просто квадрат L2 нормы, деленной на себя, т.е. dot(x, x) / dot(x, x) == 1,
В общем, для любых лагов i, j in Z, where i != j Автокорреляция в единичном масштабе dot(shift(x, i), shift(x, j)) / dot(x, x) где shift(y, n) это функция, которая сдвигает вектор y от n моменты времени и Z это набор целых чисел, так как мы говорим о реализации (теоретически, лаги могут быть в наборе действительных чисел).
Я получаю 1,0 как максимум с помощью следующего кода (начать с командной строки, как $ ipython --pylab), как и ожидалось:
In[1]: n = 1000
In[2]: x = randn(n)
In[3]: xc = correlate(x, x, mode='full')
In[4]: xc /= xc[xc.argmax()]
In[5]: xchalf = xc[xc.size / 2:]
In[6]: xchalf_max = xchalf.max()
In[7]: print xchalf_max
Out[1]: 1.0
Единственное время, когда автокорреляция лаг 0 не равна 1, это когда x нулевой сигнал (все нули).
Ответ на ваш вопрос: нет, нет функции NumPy, которая автоматически выполняет стандартизацию для вас.
Кроме того, даже если бы это было так, вам все равно пришлось бы проверять его на соответствие ожидаемому результату, и если вы могли бы сказать "Да, это правильно выполнило стандартизацию", то я бы предположил, что вы знаете, как реализовать это самостоятельно.
Я собираюсь предположить, что это может быть тот случай, когда вы неправильно реализовали их алгоритм, хотя я не уверен, так как я не знаком с ним.