Tensorflow: используйте разные выражения для прямого и обратного прохода

Question

У меня есть выражение тензорного потока, где я хочу использовать другое выражение в зависимости от того, вычисляю ли я проход вперед или назад (градиент). В частности, я хочу игнорировать эффекты некоторой случайности (шума), добавленной в сеть во время обратного прохода.

Вот упрощенный пример

import numpy as np
import tensorflow as tf

x = tf.placeholder(tf.float32)
y = x**2
u = tf.random_uniform(tf.shape(x), minval=0.9, maxval=1.1)
yu = y * u
z = tf.sqrt(yu)
g = tf.gradients(z, x)[0]

with tf.Session() as sess:
    yv, yuv, zv, gv = sess.run([y,yu,z,g], {x: [-2, -1, 1]})

print(yv)
print(yuv)
print(zv)
print(gv)

который выводит что-то вроде

[4. 1. 1.]
[4.1626534 0.9370764 1.0806011]
[2.0402582  0.96802706 1.0395197 ]
[-1.0201291  -0.96802706  1.0395197 ]

Последние значения здесь являются производными от z в отношении x, Я хотел бы, чтобы они не включали термин мультипликативного шума uт.е. они должны быть последовательно [-1, -1, 1] для этих входных значений x,

Есть ли способ сделать такую ​​вещь только с помощью Python? Я знаю, что могу сделать пользовательский оператор в C и определить собственный градиент для него, но я бы хотел избежать этого, если это возможно.

Кроме того, я надеюсь использовать это как часть слоя Keras, так что решение на основе Keras было бы альтернативой (то есть, если можно было бы определить другое выражение для прохода вперед и назад через слой Keras). Это означает, что просто определение второго выражения z2 = tf.sqrt(y) и звонит gradients однако, это не решение для меня, потому что я не знаю, как бы это выразить в Керасе (поскольку в Керасе это будет частью очень длинного вычислительного графа).

Answer 1

Короткий ответ: уловка Сергея Иоффе, о которой вы упоминали выше, будет работать только в том случае, если она будет применена в самом конце графика, прямо перед вычислением градиента.

Я предполагаю, что вы попробовали следующее, которое не будет работать:

yu_fixed = tf.stop_gradient(yu - y) + y
z = tf.sqrt(yu_fixed)

Это все еще выводит случайные градиенты.

Чтобы понять почему, давайте продолжим вычисление градиента. Давайте использовать s как сокращение для tf.stop_gradient, Это работает так, что когда TensorFlow необходимо вычислить s(expr)просто возвращается expr, но когда нужно вычислить градиент s(expr), он возвращает 0.

Мы хотим вычислить градиент z = sqrt(s(yu - y) + y), Теперь, потому что 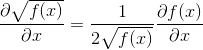мы находим, что градиент z содержит как термин с производной s(), но также термин, содержащий s() сам. Этот последний термин не обнулит s() часть, поэтому вычисленная производная z будет зависеть (каким-то странным и неправильным образом) от значения yu, Вот почему вышеупомянутое решение все еще содержит случайность в градиенте.

Насколько я понимаю, единственный способ обойти это - применить трюк Иоффе в качестве последнего этапа перед tf.gradient, Другими словами, если вы сделаете что-то вроде следующего, вы получите ожидаемый результат:

x = tf.placeholder(tf.float32)
y = x**2
u = tf.random_uniform(tf.shape(x), minval=0.9, maxval=1.1)
yu = y * u
z = tf.sqrt(yu)
z_fixed = tf.stop_gradient(z - tf.sqrt(y)) + tf.sqrt(y)
g = tf.gradients(z_fixed, x)[0]

with tf.Session() as sess:
    yv, yuv, zv, gv = sess.run([y,yu,z_fixed,g], {x: [-2, -1, 1]})

print(yv)
print(yuv)
print(zv)
print(gv)

Выход:

[ 4.  1.  1.]
[ 3.65438652  1.07519293  0.94398856]
[ 1.91164494  1.03691506  0.97159076]
[-1. -1.  1.]