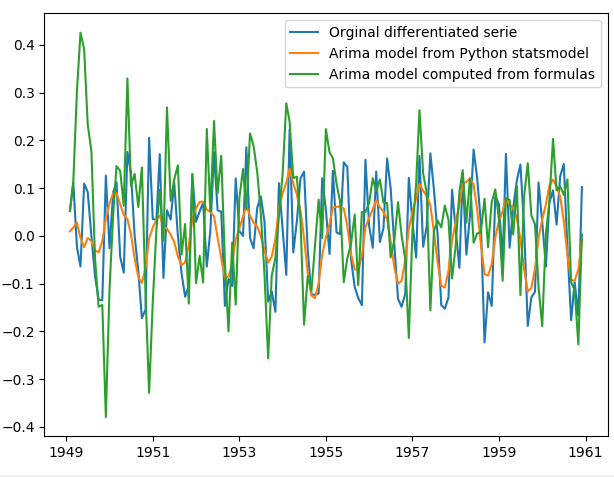
Почему модель Arima из Python statsmodel возвращает результаты, отличные от Arima из аналитической формулы

Question

Я новичок в моделях Arima. Я работал с библиотекой Python: statsmodel, в частности с функцией Arima, получая следующие результаты для следующего фрагмента кода:

model = ARIMA(ts_log, order=(2, 1, 2))
results_ARIMA = model.fit(disp=False, transparams=True, trend='c',solver='newton')
predictions_ARIMA_diff = pd.Series(results_ARIMA.fittedvalues, copy=True)

plt.plot(ts_log -ts_log.shift(),label='Orginial differentiated serie')
plt.plot(predictions_ARIMA_diff, label ='Arima model from Python statsmodel')

Я хочу быть способным воспроизводить результаты графика, данные Python, поэтому я реализовал функцию для вычисления модели Arima, используя конкретные значения параметров. Это функция:

def ARIMA_from_parameters (alpha,beta,mu, TS,possible_noise=[]): #N = numero de medidas que quieres preveer
    TSdif = TS - TS.shift() # La primera que se forma es NaN
    TSdif.dropna(inplace=True) # Me la cargo

    Arima =[]
    p = len(alpha)
    q = len(beta)
    maxpq = max([p,q])

    noise = [gauss(0.0, 0.084) for i in range(0, len(TSdif))]  # S.D of innovations = 0.084

    #Initial terms
    for i in range(0,maxpq):
        Arima.append(TSdif[i])

    #Rest of terms
    for i in range(maxpq,len(TSdif)):
        sum_p = 0
        cnt_p = 0
        for e in alpha:
            cnt_p = cnt_p +1
            sum_p = sum_p +e*Arima[i-cnt_p]

        sum_q = 0
        cnt_q = 0

        sum_q =sum_q + noise[i]
        for e in beta:
            cnt_q = cnt_q + 1
            sum_q = sum_q + e * noise[i - cnt_q]

        Yt = sum_p + sum_q + mu
        Arima.append(Yt)

    #Transform to TS:
    Arima_TS = pd.Series(Arima, index=TSdif.index)

    return Arima_TS

Использование последней функции с теми же параметрами, что и у подобранной модели Arima, и вычисление шума, подобного гауссову, со средним значением 0 и стандартным значением, равным "SD инноваций" для подобранной модели (0,084), не только возвращает другие результаты, но и результат, заданный Python не использует начальные условия, как функция.

Кто-нибудь может пролить свет на этот вопрос?