Моделирование рассеивающей среды

Question

У меня есть модель рассеяния света, как:

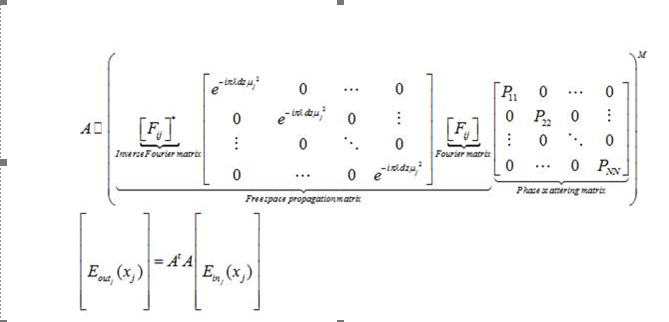
A является оператором, который является матрицей фазового рассеяния, сопровождаемой Eout=AtraXAXEin;, Ein это мой вклад.

Я предположил 5 таких слоев. Таким образом, каждый слой представляет собой матрицу фазового рассеяния, за которой следует небольшое угловое распространение поля. У меня зеркало после рассеивающей среды очень близко к среде. Теперь, как и ожидалось, поле будет проходить через ту же среду, и у нас есть вывод, как Eout=AtraXAXEin;

Я приложил код для модели. Не могли бы вы проверить, если я прав? Пожалуйста, просмотрите комментарии, в которых я выразил свои сомнения в коде.

clear all
close all

%Scattering Medium Modelling
Ein=rand(256,256).*exp(1i*2*pi*rand(256,256)); %define a random input

%Forward Scattering consist of 5 layers (each layer Phase scattering Matrix
%multiplied by Angular spectrum propagation
for k=1:5
    T(:,:,k)=rand(256,256).*exp(1i*2*pi*rand(256,256));      %phase scattering matrix    
    image=T(:,:,k).*Ein %input times Phase scattering matrix
    u=Angular_Spectrum_Propagation(image,1e-4,.532e-6,9e-6); % followed by angular spectrum propagation.
    % figure
    % imshow(abs(u),[])
    Ein=u;
    % A=u*Einv;
end

tempu=u;
figure
imshow(abs(u),[])

% tempu is the field that hits the mirror, am I correct?

% now the light hits the mirror and goes back through same medium.
for k=5:-1:1 
    u=Angular_Spectrum_Propagation(tempu,-1e-4,.532e-6,9e-6); % is negative distance correct  while the light is travelling back??
    Eout=u.*T(:,:,k);
    tempu=Eout;
    % figure
    % imshow(abs(Eout),[])
    % Ein=u;
    % A=u*Einv;
end

figure
imshow(abs(Eout),[])

Обратите внимание, что вам нужна функция Angular_Spectrum_Propagation запустить его, который приведен ниже:

%Purpose: propagation of the wave by using the Angular Spectrum Method
%'Inputs': 'Comp_Amp0',the input complex amplitude of the object wave;
%'d', propagation distance('m');
%'Pixel', pixel size of input object wave;
%'Outputs': 'Comp_Amp,Complex amplitude of the propagated object wave;
%'H', Propagation core to check the correctness of the method;

function [Comp_Amp,H]=Angular_Spectrum_Propagation(Comp_Amp0,d,lambda,Pixel)

k=2*pi/lambda; %Wave vector;

%Coordinates in Fourier plane;
[y_length,x_length]=size(Comp_Amp0); %The size of interferogram;
u_max=1/Pixel; %The maximal frequency;
v_max=1/Pixel; %The maximal frequency;
u=linspace(-u_max/2,u_max/2,x_length); %coordinate in x direction  (Unit:1/m);
v=linspace(-v_max/2,v_max/2,y_length); %coordinate in y direction  (Unit:1/m);
[uu,vv]=meshgrid(u,v); %Two dimensional frequency (Unit: 1/m);

%Propagation with ASP:
Freq=fftshift(fft2(fftshift(Comp_Amp0)));  %Frequency spectrum;
H=exp(1i*k*d*sqrt( abs(1-(lambda*uu).^2-(lambda*vv).^2 ))); %Wave function for plane wave (uu,vv); %%-->Note: h only relys on the piexl size of image;
Comp_Amp=fftshift( ifft2(fftshift(Freq.*H)) );  %Reconstructed object wave;

end

%Note: the units of the inputs can be 'm' or 'mm';