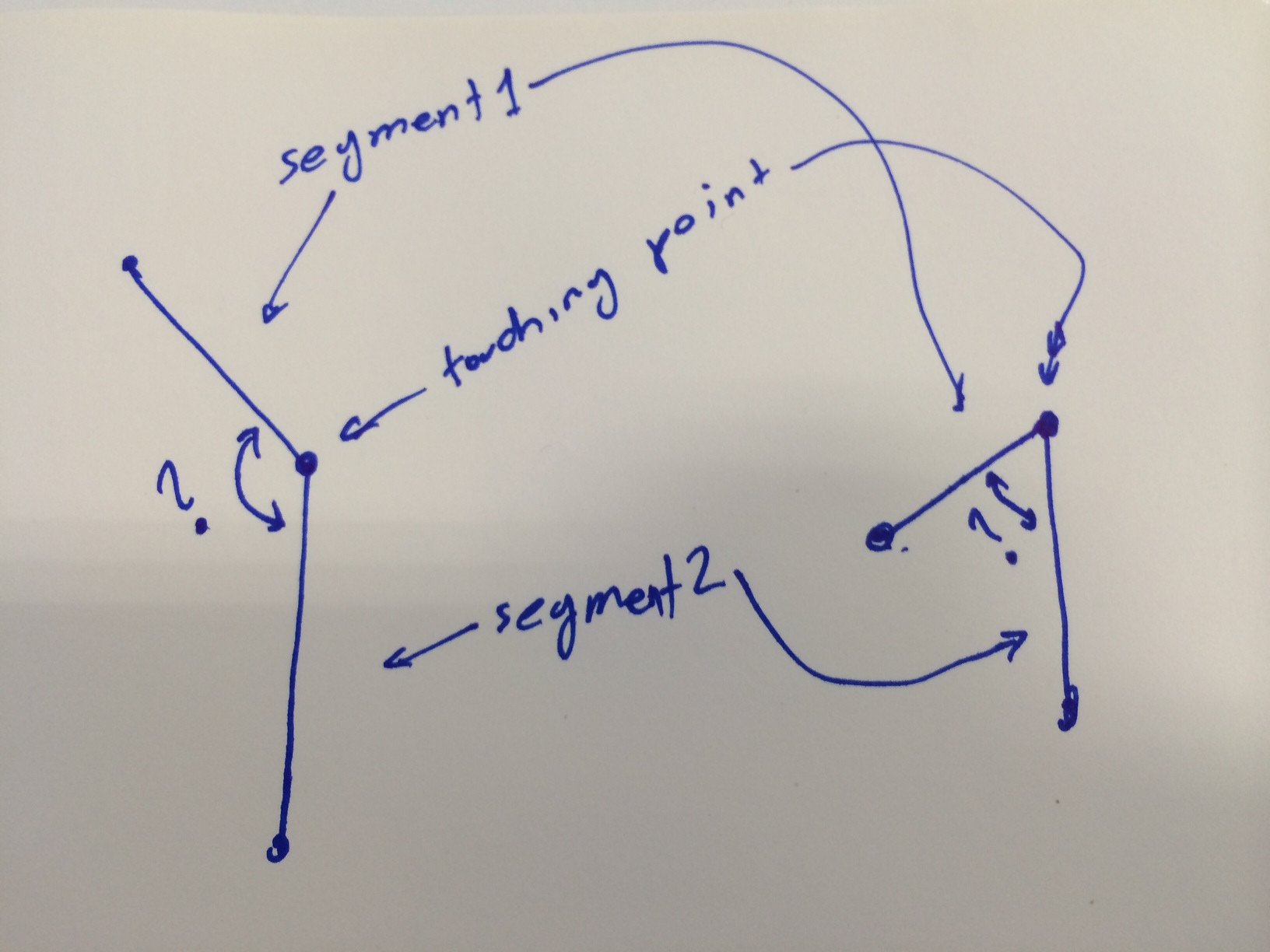
Угол менее 180 между двумя сегментами (линиями)

Question

Мне нужно найти "внутренний" угол в градусах между двумя сегментами (линиями), то есть менее 180 градусов. Любой быстрый способ сделать это в python2.7? (Shapely, кажется, не имеет функции для этого)

сегмент1 равен x1, y1, x2, y2

сегмент2 - это х3, у3, х4, у4

Answer 1

Первоначально я предложил использовать закон косинусов в векторной форме: если два отрезка линии заданы векторами b и c, а угол между ними равен θ, то

b · c = |б| |с| cos θ

так что

θ = cos −¹((b · c) / |b| |c|)

Но, как отмечает Алекс Вена в комментариях, это дает плохие результаты, когда θ близко к нулю:

>>> theta = 1e-6
>>> a = Vector(1, 0)
>>> b = Vector(cos(theta), sin(theta))
>>> acos(a.dot(b) / (a.length * b.length))
9.999334257726859e-07
>>> abs(theta - _) / theta
6.657422731408927e-05

что является относительной ошибкой в ​​достижении одной части из десяти тысяч. Для очень маленьких углов вы можете получить относительную погрешность 100%:

>>> theta = 1e-9
>>> a = Vector(1, 0)
>>> b = Vector(cos(theta), sin(theta))
>>> acos(a.dot(b) / (a.length * b.length))
0.0

Альтернативная формула использует арктангенс вместо арккосинуса:

θ = tan⁻¹(|a × b| / (a · b))

и это дает более точный результат для малых углов:

>>> atan2(abs(a.cross(b)), a.dot(b))
1e-09
>>> theta == _
True

(Альтернативная формула следует из свойства перекрестного произведения, что |a × b| = |a| |b| sin θ. Разделите это по закону косинусов, чтобы получить результат, используемый здесь.)