Фильтр Калмана (pykalman): значение для obs_covariance и модели без перехвата
Я смотрю на KalmanFilter от pykalman, показанный в примерах:
и мне интересно
observation_covariance=100,
vs
observation_covariance=1,
документация гласит
observation_covariance R: e(t)^2 ~ Gaussian (0, R)
Как правильно установить значение здесь?
Кроме того, возможно ли применить фильтр Калмана без перехвата в вышеупомянутом модуле?
1 ответ
Ковариация наблюдений показывает, как много ошибок вы предполагаете в своих входных данных. Фильтр Калмана отлично работает на нормально распределенных данных. В этом предположении вы можете использовать правило 3-сигма для расчета ковариации (в данном случае дисперсии) вашего наблюдения на основе максимальной ошибки в наблюдении.
Значения в вашем вопросе можно интерпретировать следующим образом:
Пример 1
observation_covariance = 100
sigma = sqrt(observation_covariance) = 10
max_error = 3*sigma = 30
Пример 2
observation_covariance = 1
sigma = sqrt(observation_covariance) = 1
max_error = 3*sigma = 3
Поэтому вам нужно выбрать значение на основе ваших данных наблюдений. Чем точнее наблюдение, тем меньше ковариация наблюдения.
Еще один момент: вы можете настроить свой фильтр, манипулируя ковариацией, но я думаю, что это не очень хорошая идея. Чем выше значение ковариации наблюдения, тем слабее влияние нового наблюдения на состояние фильтра.
Извините, я не понял вторую часть вашего вопроса (про фильтр Калмана без перехвата). Не могли бы вы объяснить, что вы имеете в виду? Вы пытаетесь использовать регрессионную модель, и к ней принадлежат как точка пересечения, так и наклон.
---------------------------
ОБНОВИТЬ
Я подготовил некоторый код и графики, чтобы подробно ответить на ваши вопросы. Я использовал исторические данные EWC и EWA, чтобы приблизиться к исходной статье.
Прежде всего, вот код (почти такой же, как в приведенных выше примерах, но с другой нотацией)
from pykalman import KalmanFilter
import numpy as np
import matplotlib.pyplot as plt
# reading data (quick and dirty)
Datum=[]
EWA=[]
EWC=[]
for line in open('data/dataset.csv'):
f1, f2, f3 = line.split(';')
Datum.append(f1)
EWA.append(float(f2))
EWC.append(float(f3))
n = len(Datum)
# Filter Configuration
# both slope and intercept have to be estimated
# transition_matrix
F = np.eye(2) # identity matrix because x_(k+1) = x_(k) + noise
# observation_matrix
# H_k = [EWA_k 1]
H = np.vstack([np.matrix(EWA), np.ones((1, n))]).T[:, np.newaxis]
# transition_covariance
Q = [[1e-4, 0],
[ 0, 1e-4]]
# observation_covariance
R = 1 # max error = 3
# initial_state_mean
X0 = [0,
0]
# initial_state_covariance
P0 = [[ 1, 0],
[ 0, 1]]
# Kalman-Filter initialization
kf = KalmanFilter(n_dim_obs=1, n_dim_state=2,
transition_matrices = F,
observation_matrices = H,
transition_covariance = Q,
observation_covariance = R,
initial_state_mean = X0,
initial_state_covariance = P0)
# Filtering
state_means, state_covs = kf.filter(EWC)
# Restore EWC based on EWA and estimated parameters
EWC_restored = np.multiply(EWA, state_means[:, 0]) + state_means[:, 1]
# Plots
plt.figure(1)
ax1 = plt.subplot(211)
plt.plot(state_means[:, 0], label="Slope")
plt.grid()
plt.legend(loc="upper left")
ax2 = plt.subplot(212)
plt.plot(state_means[:, 1], label="Intercept")
plt.grid()
plt.legend(loc="upper left")
# check the result
plt.figure(2)
plt.plot(EWC, label="EWC original")
plt.plot(EWC_restored, label="EWC restored")
plt.grid()
plt.legend(loc="upper left")
plt.show()
Я не мог получить данные, используя панд, поэтому я скачал их и прочитал из файла.
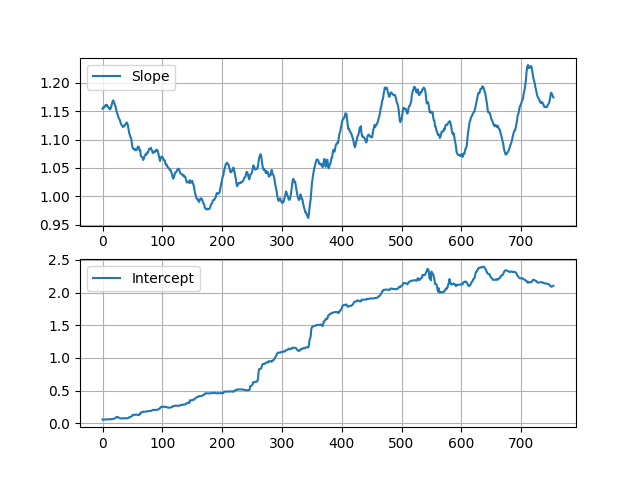
Здесь вы можете увидеть предполагаемый уклон и перехват:
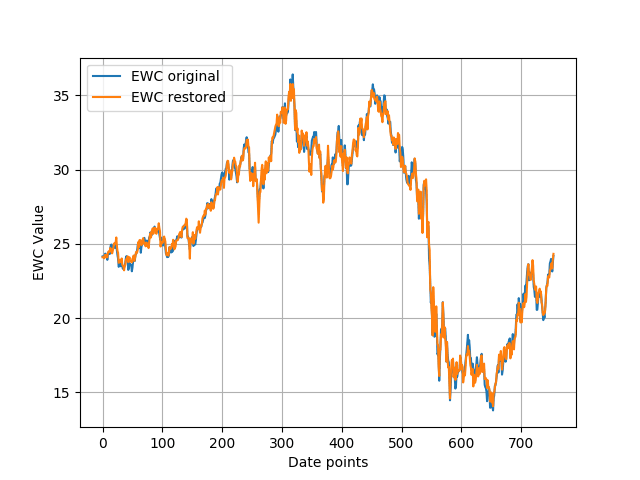
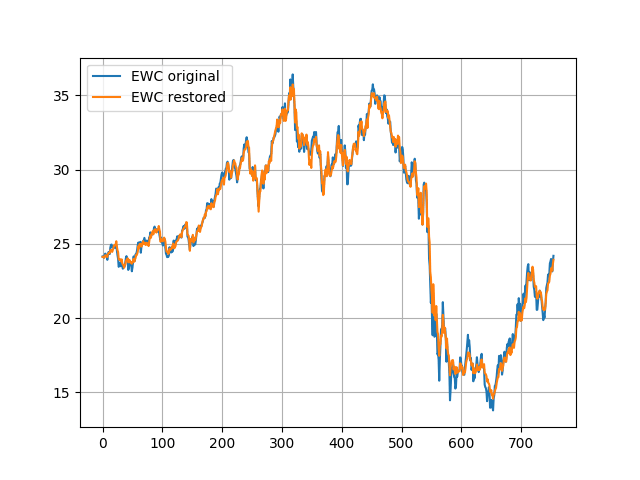
Чтобы проверить оценочные данные, я восстановил значение EWC из EWA, используя оценочные параметры:
О значении ковариации наблюдения
Изменяя значение ковариации наблюдения, вы сообщаете фильтру, насколько точны входные данные (обычно вы просто описываете свою уверенность в наблюдении, используя некоторые таблицы данных или свои знания о системе).
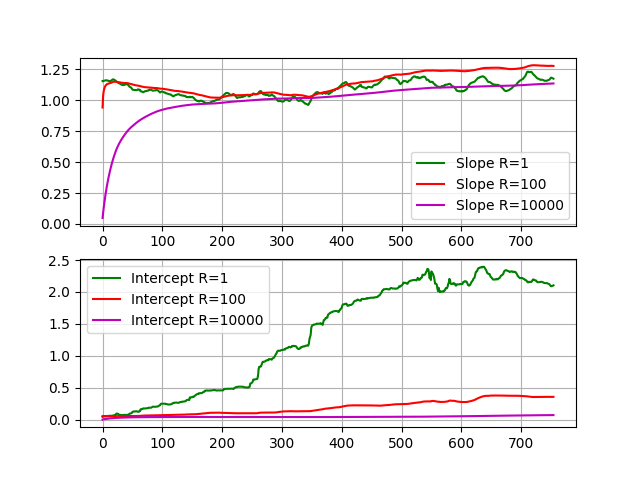
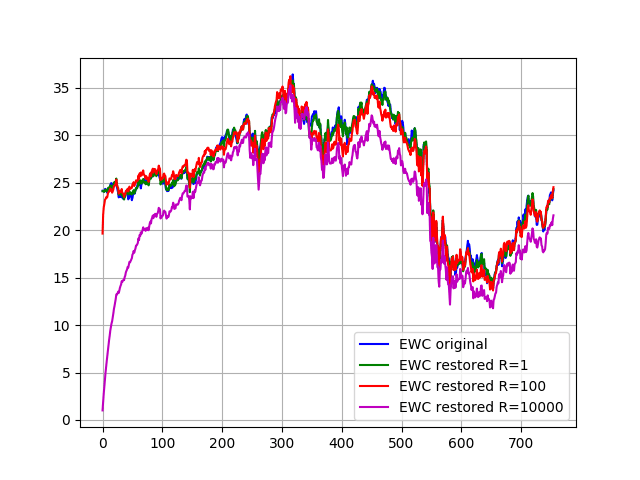
Вот оценочные параметры и восстановленные значения EWC с использованием различных значений ковариации наблюдения:
Вы можете видеть, что фильтр лучше следует исходной функции с большей уверенностью в наблюдении (меньше R). Если достоверность низкая (больше R), фильтр оставляет первоначальную оценку (наклон = 0, пересечение = 0) очень медленно, и восстановленная функция находится далеко от исходной.
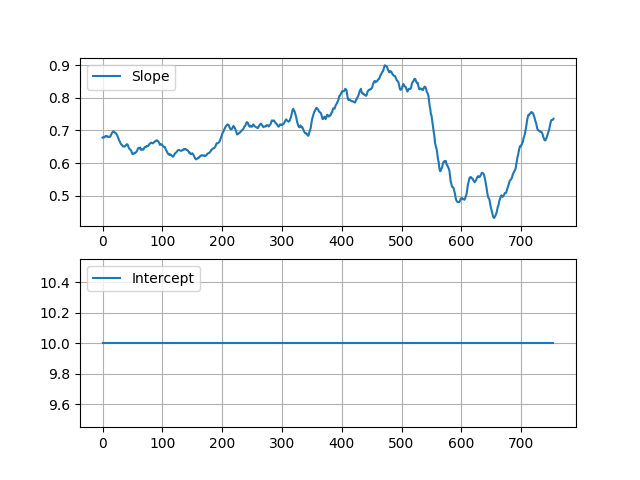
О замороженном перехвате
Если вы хотите заморозить перехват по какой-то причине, вам нужно изменить всю модель и все параметры фильтра.
В обычном случае у нас было:
x = [slope; intercept] #estimation state
H = [EWA 1] #observation matrix
z = [EWC] #observation
Теперь у нас есть:
x = [slope] #estimation state
H = [EWA] #observation matrix
z = [EWC-const_intercept] #observation
Результаты:
Вот код:
from pykalman import KalmanFilter
import numpy as np
import matplotlib.pyplot as plt
# only slope has to be estimated (it will be manipulated by the constant intercept) - mathematically incorrect!
const_intercept = 10
# reading data (quick and dirty)
Datum=[]
EWA=[]
EWC=[]
for line in open('data/dataset.csv'):
f1, f2, f3 = line.split(';')
Datum.append(f1)
EWA.append(float(f2))
EWC.append(float(f3))
n = len(Datum)
# Filter Configuration
# transition_matrix
F = 1 # identity matrix because x_(k+1) = x_(k) + noise
# observation_matrix
# H_k = [EWA_k]
H = np.matrix(EWA).T[:, np.newaxis]
# transition_covariance
Q = 1e-4
# observation_covariance
R = 1 # max error = 3
# initial_state_mean
X0 = 0
# initial_state_covariance
P0 = 1
# Kalman-Filter initialization
kf = KalmanFilter(n_dim_obs=1, n_dim_state=1,
transition_matrices = F,
observation_matrices = H,
transition_covariance = Q,
observation_covariance = R,
initial_state_mean = X0,
initial_state_covariance = P0)
# Creating the observation based on EWC and the constant intercept
z = EWC[:] # copy the list (not just assign the reference!)
z[:] = [x - const_intercept for x in z]
# Filtering
state_means, state_covs = kf.filter(z) # the estimation for the EWC data minus constant intercept
# Restore EWC based on EWA and estimated parameters
EWC_restored = np.multiply(EWA, state_means[:, 0]) + const_intercept
# Plots
plt.figure(1)
ax1 = plt.subplot(211)
plt.plot(state_means[:, 0], label="Slope")
plt.grid()
plt.legend(loc="upper left")
ax2 = plt.subplot(212)
plt.plot(const_intercept*np.ones((n, 1)), label="Intercept")
plt.grid()
plt.legend(loc="upper left")
# check the result
plt.figure(2)
plt.plot(EWC, label="EWC original")
plt.plot(EWC_restored, label="EWC restored")
plt.grid()
plt.legend(loc="upper left")
plt.show()