Как реализовать лабиринт, используя непересекающиеся множества?
Вот класс DisjointSet, который я использую:
public class DisjointSet{
public DisjointSet(int size){
s = new int[size];
for(int i = 0; i < size; ++i){
s[i] = -1;
}
}
public void union(int el1, int el2){
int root1 = find(el1);
int root2 = find(el2);
if(root1 == root2){
return;
}
if(s[root2] < s[root1]){
s[root1] = root2;
}
else{
if(s[root1] == s[root2]){
--s[root1];
}
s[root2] = root1;
}
}
public int find(int x){
if(s[x] < 0){
return x;
}
else{
s[x] = find(s[x]);
return s[x];
}
}
private int[] s;
}
И вот мой класс лабиринта:
public class Maze
{
public Vector<Wall> maze;
public Vector<Room> graph;
public Vector<Integer> path;
public int LASTROOM;
public int height;
public int width;
public Random generator;
public DisjointSet ds;
public int dsSize;
public Maze(int w, int h, int seed)
{
width = w;
height = h;
dsSize = width * height;
LASTROOM = dsSize-1;
// Maze initialization with all walls
maze = new Vector<Wall>();
for(int i = 0; i < height; ++i)
{
for(int j = 0; j < width; ++j)
{
if(i > 0)
maze.add(new Wall(j+i*height, j+(i-1)*height));
if(j > 0)
maze.add(new Wall(j+i*height, j-1+i*height));
}
}
// Creation of the graph topology of the maze
graph = new Vector<Room>();
for(int i = 0; i < dsSize; ++i)
graph.add(new Room(i));
// Sort the walls of random way
generator = new Random(seed);
for(int i = 0; i < maze.size(); ++i)
{
//TODO
}
// Initialization of related structures
ds = new DisjointSet(dsSize);
path = new Vector<Integer>();
}
public void generate()
{
//TODO
}
public void solve()
{
//TODO
}
}
Я долго искал способ реализации generate() и solve() вместе со случайной сортировкой стен лабиринта, и я не могу найти какой-либо алгоритм или реализацию в Интернете, чтобы сделать это,
Функция generate() должна пройти через переставленные стены в переменной лабиринта и уничтожить ее, если две части (комнаты), соединенные стеной, уже не находятся в одном наборе. Метод также должен добавить ребро в графе комнаты (в каждой комнате есть список смежных именованных путей, а в классе комнаты есть переменная id, которая идентифицирует вершины каждого графа).
solve() должен решить путь лабиринта и сгенерировать вектор класса Лабиринт, содержащий порядок комнат, через которые нужно пройти, чтобы добраться до выхода. Первая комната расположена в 0, а последняя комната в LASTROOM.
Примечание: конструкторы лабиринта и комнаты:
public Wall(int r1, int r2)
{
room1 = r1;
room2 = r2;
}
public Room(int i)
{
id = i;
distance = -1;
paths = new Vector<Integer>();
}
Если кто-то будет достаточно любезен, предложит реализацию, которая будет работать на Java, я был бы очень признателен, спасибо.
1 ответ
Прежде всего, мне очень нравится идея лабиринтов, и я работаю над аналогичным проектом на Java с созданием Torus Mazes.
Чтобы создать свой лабиринт, вам нужно взглянуть на это ключевое предложение:
... каждая комната имеет список смежных именованных путей, а класс Room имеет переменную id, которая идентифицирует вершины каждого графа
Что это говорит нам? Это говорит нам о структуре данных, которая нам нужна! Когда вы имеете дело с такими проблемами, как это; смежные векторы, соединенные ребрами, вы, несомненно, собираетесь создать список смежности.
Есть несколько разных способов сделать это, но, безусловно, самый простой (и, возможно, наиболее эффективный в этом случае) - это создать массив связанных списков. Это список смежности, который я создал без использования встроенных структур из библиотек Java, но ту же логику можно использовать, если вы решите использовать LinkedList<> встроенный.
/*
* The Node class creates individual elements that populate the
* List class. Contains indexes of the node's neighbors and their
* respective edge weights
*/
class Node {
public int top;
public int topWeight;
public int bottom;
public int bottomWeight;
public int left;
public int leftWeight;
public int right;
public int rightWeight;
public int numConnec;
// Default constructor, ititializes neghbors to -1 by default and edge
// weights to 0
Node () {
top = -1;
right = -1;
bottom = -1;
left = -1;
}
} // End Node class
/*
* The List class contains Nodes, which are linked to one another
* to create a Linked List. Used as an adjacency list in the
* UnionFind class
*/
class List {
public Node neighbors;
// Default constructor
List () {
neighbors = new Node ();
}
/**
* Generates valid edges for the node, also assigns a randomly generated weight to that edge
* @param i The row that the node exists on, used to generate outer-node edges
* @param j The index of the node in the maze from 0 to (2^p)^2 - 1
* @param twoP Represents the dimensions of the maze, used in calculating valid edges
* @param choice Randomly generated number to choose which edge to generate
* @param weight Randomly generated number to assign generated edge a weight
* @return If the assignment was done correctly, returns true. Else returns false.
*/
public boolean validEdges (int i, int j, int twoP, int choice, int weight) {
if (neighbors.numConnec < 4) {
// Top
if (choice == 0) {
neighbors.top = generateTop(i, j, twoP);
neighbors.topWeight = weight;
neighbors.numConnec++;
}
// Right
else if (choice == 1) {
neighbors.right = generateRight(i, j, twoP);
neighbors.rightWeight = weight;
neighbors.numConnec++;
}
// Bottom
else if (choice == 2) {
neighbors.bottom = generateBottom(i, j, twoP);
neighbors.bottomWeight = weight;
neighbors.numConnec++;
}
// Left
else if (choice == 3) {
neighbors.left = generateLeft(i, j, twoP);
neighbors.leftWeight = weight;
neighbors.numConnec++;
}
}
else {
return false;
}
return true;
}
public int generateTop (int i, int j, int twoP) {
int neighbor = 0;
// Set the top neighbor
if (i == 0) {
neighbor = j + twoP * (twoP + (-1));
}
else {
neighbor = j + (-twoP);
}
return neighbor;
}
public int generateRight (int i, int j, int twoP) {
int neighbor = 0;
// Set the right neighbor
if (j == twoP * (i + 1) + (-1)) {
neighbor = twoP * i;
}
else {
neighbor = j + 1;
}
return neighbor;
}
public int generateBottom (int i, int j, int twoP) {
int neighbor = 0;
// Set the bottom neighbor
if (i == twoP + (-1)) {
neighbor = j - twoP * (twoP + (-1));
}
else {
neighbor = j + twoP;
}
return neighbor;
}
public int generateLeft (int i, int j, int twoP) {
int neighbor = 0;
// Set the left neighbor
if (j == twoP * i) {
neighbor = twoP * (i + 1) + (-1);
}
else {
neighbor = j + (-1);
}
return neighbor;
}
} // End List class
Чтобы решить лабиринт, это звучит как проблема, которую может решить реализация алгоритма Дейкстры.
Дейкстра работает, начиная с вашего первого узла, чтобы создать известный набор. Затем вы определяете кратчайший путь к следующему ребру и добавляете этот узел к известному набору. Каждый раз, когда вы ищите следующий кратчайший путь, вы добавляете расстояние, пройденное от первого узла.
Этот процесс продолжается до тех пор, пока все узлы не окажутся в известном наборе и не будет рассчитан кратчайший путь к вашей цели.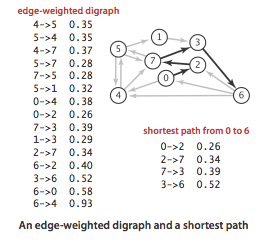
Кратчайшие пути