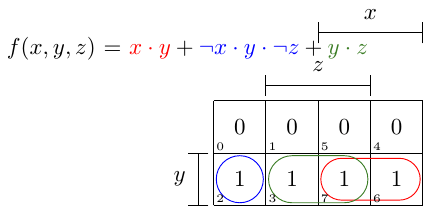K-Map для решения алгебраической редукции

Question

Мне нужна помощь в проверке алгебраического выражения с использованием K-Map.

Выражение, которое я публикую, на самом деле было написано моим профессором, но для практических целей я хотел использовать K-Map, чтобы убедиться, что ответ правильный.

   ->  X • Y + X' • Y • Z' + Y • Z =
   ->  X • Y •(Z + Z') + X' • Y • Z' + Y • Z =
   ->  X•Y•Z + X•Y•Z' + X'•Y•Z' + Y• Z =
   ->  X•Y•Z + Y•Z' • (X + X') + Y•Z =
   ->  X•Y•Z + Y•Z' + Y•Z =
   ->  X•Y•Z + Y•(Z' + Z) =
   ->  X•Y•Z + Y=
   ->  Y•(X•Z + 1)= Y

Когда я попробовал свое решение K-Map, чтобы доказать правильный ответ, я придумал это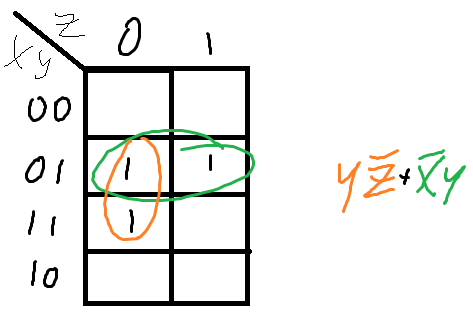

YZ' + X'Y

Я не уверен, что мой ответ правильный или нет. Если это не так, мне нужно, чтобы кто-то показал мне, как это исправить, чтобы оно соответствовало решению, которое я опубликовал. Я ценю помощь.

Answer 1

Помните, что 1 входит в K-карту тогда и только тогда, когда выражение не меняется и совпадает либо с двумя 0, либо с двумя 1. Выражение не существует, когда оно изменяется или имеет 0 и 1 вместе.

Так что это моя K-Map и то, что я сделал.

KMAP

Мой ответ появился как Y, что также соответствует ответу вашего профессора.

(Изменить: я забыл поставить плюсы в уравнении, но я надеюсь, что вы поняли идею)

Answer 2

Выводы и ответы, данные вашим профессором, верны (каждый шаг). Поэтому ваш ответ, будучи другим, не верен. Возьмите для примера X = Y = Z = 1, Исходное выражение оценивается следующим образом

X • Y + X' • Y • Z' + Y • Z = 1 • 1 + 0 • 1 • 0 + 1 • 1
                            = 1 + 0 + 1
                            = 1 

Тем не мение,

Y • Z' + X' • Y  = 1 • 0 + 0 • 1
                 = 0 + 0
                 = 0

который отличается от исходного выражения, а также от его эквивалента Y,

Answer 3

Вы можете разбить данную функцию в виде SOP (DNF) на отдельные термины и найти их на K-карте. Это действительно как перекрещивание.

Имея функцию:

f(x,y,z) = x·y + ¬x·y·¬z + y·z

где:

• x·y клетки, где x является true и y является true; отмечен красным;

• ¬x·y·¬z клетки, где x а также z являются false и y является true; отмечен синим цветом; поскольку он использует все заданные переменные, этот термин также является обозначением, обозначающим только одну ячейку;

• y·z ~ клетки, где оба y а также z являются true; отмечен зеленым

Вы можете видеть, что отмеченные клетки могут быть сгруппированы в более крупные 2^i размер пузыря, а 2^2=4 один.

И вы должны использовать это вместо трех продуктов в исходной функции, потому что чем меньше переменных и операторов, тем легче работать с выражением.

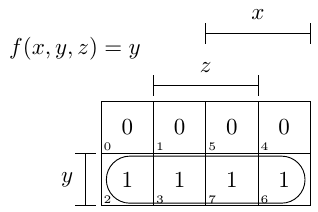
Обойдя как можно большую группу, вы получите тот же результат, что и ваш учитель.

f(x,y,z) = x·y + ¬x·y·¬z + y·z = y

Как вы можете видеть, логическое значение выражения в 50 процентах случаев оценивается как истинное, а в остальных 50 процентах ложное, поскольку значение зависит только от значения переменной. y,