Нахождение вектора, который примерно одинаково удален от всех векторов в наборе

Question

У меня есть набор из 3 миллионов векторов (по 300 измерений каждый), и я ищу новую точку в этом 300 тусклом пространстве, которая примерно одинаково удалена от всех других точек (векторов)

Что я мог сделать, так это инициализировать случайный вектор v и запустить оптимизацию по v с целью: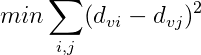

Где d_xy - это расстояние между вектором x и вектором y, но это будет очень затратно для вычислений.

Я ищу приблизительный вектор решения этой проблемы, который можно быстро найти на очень больших наборах векторов. (Или любые библиотеки, которые будут делать что-то подобное для меня - любой язык)

Answer 1

Я согласен, что в целом это довольно сложная проблема оптимизации, особенно в масштабах, которые вы описываете. Каждая оценка целевой функции требует O(нм + n^2) работы для n точек измерения m - O(нм) для вычисления расстояний от каждой точки до новой точки и O(n^2) для вычисления цели с учетом расстояний, Это довольно страшно, когда m=300 и n=3M. Таким образом, даже одна функция оценки, вероятно, трудно, не говоря уже о решении полной проблемы оптимизации.

Один из подходов, который был упомянут в другом ответе, состоит в том, чтобы взять центр тяжести точек, который можно эффективно вычислить, - O(нм). Недостатком этого подхода является то, что он может сделать ужасно в предложенной цели. Например, рассмотрим ситуацию в одномерном пространстве с 3 миллионами точек со значением 1 и 1 точкой со значением 0. По результатам проверки оптимальным решением является v=0,5 с объективным значением 0 (это равноудалено от каждой точки), но центроид выберет v=1 (ну, чуть-чуть меньше) с объективным значением 3 миллиона.

Подход, который, я думаю, будет лучше, чем центроид, - оптимизировать каждое измерение отдельно (игнорируя существование других измерений). В то время как целевая функция все еще является дорогой для вычисления в этом случае, немного алгебры показывает, что производная цели довольно легко вычислить. Это сумма по всем парам (i, j), где i v значения 4*((vi)+(vj)). Помните, что мы оптимизируем одно измерение, чтобы точки i и j были одномерными, как и v. Поэтому для каждого измерения мы можем отсортировать данные (O(n lg n)) и затем вычислить производную для значения v в O(n) время с использованием бинарного поиска и базовой алгебры. Затем мы можем использовать scipy.optimize.newton найти ноль производной, которая будет оптимальным значением для этого измерения. Итерируя по всем измерениям, у нас будет приблизительное решение нашей проблемы.

Сначала рассмотрим предложенный подход по сравнению с методом центроида в простой настройке с одномерными точками данных {0, 3, 3}:

import bisect
import scipy.optimize

def fulldist(x, data):
    dists = [sum([(x[i]-d[i])*(x[i]-d[i]) for i in range(len(x))])**0.5 for d in data]
    obj = 0.0
    for i in range(len(data)-1):
        for j in range(i+1, len(data)):
            obj += (dists[i]-dists[j]) * (dists[i]-dists[j])
    return obj

def f1p(x, d):
    lownum = bisect.bisect_left(d, x)
    highnum = len(d) - lownum
    lowsum = highnum * (x*lownum - sum([d[i] for i in range(lownum)]))
    highsum = lownum * (x*highnum - sum([d[i] for i in range(lownum, len(d))]))
    return 4.0 * (lowsum + highsum)

data = [(0.0,), (3.0,), (3.0,)]
opt = []
centroid = []
for d in range(len(data[0])):
    thisdim = [x[d] for x in data]
    meanval = sum(thisdim) / len(thisdim)
    centroid.append(meanval)
    thisdim.sort()
    opt.append(scipy.optimize.newton(f1p, meanval, args=(thisdim,)))
print "Proposed", opt, "objective", fulldist(opt, data)
# Proposed [1.5] objective 0.0
print "Centroid", centroid, "objective", fulldist(centroid, data)
# Centroid [2.0] objective 2.0

Предложенный подход находит точное оптимальное решение, в то время как метод центроида немного пропускает.

Рассмотрим чуть более крупный пример с 1000 точками измерения 300, каждая из которых нарисована из гауссовой смеси. Значение каждой точки обычно распределяется со средним значением 0 и дисперсией 1 с вероятностью 0,1 и обычно распределяется со средним значением 100 и дисперсией 1 с вероятностью 0,9:

data = []
for n in range(1000):
    d = []
    for m in range(300):
        if random.random() <= 0.1:
            d.append(random.normalvariate(0.0, 1.0))
        else:
            d.append(random.normalvariate(100.0, 1.0))
    data.append(d)

Полученные в результате объективные значения составили 1,1e6 для предложенного подхода и 1,6e9 для центроидного подхода, что означает, что предлагаемый подход уменьшил цель более чем на 99,9%. Очевидно, что различия в объективном значении сильно зависят от распределения точек.

Наконец, чтобы протестировать масштабирование (удалив окончательные расчеты объективных значений, поскольку они в общем неразрешимы), я получил следующее масштабирование с m=300: 0,9 секунды для 1000 точек, 7,1 секунды для 10 000 точек и 122,3 секунды для 100 000 точки. Поэтому я ожидаю, что это займет около 1-2 часов для вашего полного набора данных с 3 миллионами точек.

Answer 2

Из этого вопроса по математике StackExchange:

Не существует точки, которая равноудалена от 4 или более точек общего положения на плоскости или n+2 точек в n измерениях.

Критерии для представления набора баллов по одной точке рассматриваются в статистике, машинном обучении и информатике. Центроид является оптимальным выбором в смысле наименьших квадратов, но есть много других возможностей.

Центроид - это точка C на плоскости, для которой сумма квадратов расстояний $\sum |CP_i|^2$ минимальна. Можно также оптимизировать другую меру центральности или настаивать на том, чтобы представителем была одна из точек (например, теоретико-графический центр взвешенного остовного дерева), или каким-либо образом назначать веса точкам и брать центр тяжести этих точек.,

Обратите внимание, в частности, "центроид является оптимальным выбором в смысле наименьших квадратов", поэтому оптимальным решением для вашей функции стоимости (которая является стоимостью наименьших квадратов) является просто усреднить все координаты ваших точек (что даст ты центроид).