Отсечение двух 2D треугольников

Question

Я знаю, что существуют эффективные алгоритмы отсечения полигонов (например, Maillot, Vatti, Greiner-Hormann). Однако эти алгоритмы работают для произвольных многоугольников, и, хотя они подходят для моего случая, мне кажется, что использование таких общих алгоритмов для простого случая, такого как мой, является излишним.

У меня есть два 2D треугольника (см. Рисунок ниже), которые я хочу обрезать один против другого. Поиск в сети не нашел ничего, кроме общих алгоритмов отсечения полигонов.

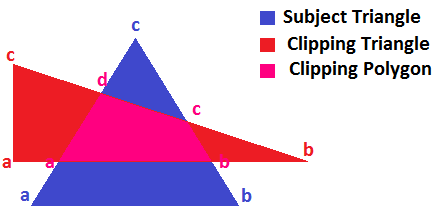
Вопрос: существует ли специализированный алгоритм для отсечения двух 2D треугольников?

Answer 1

Для двух выпуклых форм традиционный подход - это просто Сазерленд Коэн, но с большим или меньшим количеством флагов.

Например, в вашем случае:

• синий A находится снаружи красного AB, но внутри двух других красных краев; введите код 100;
• синий B такой же; введите код 100;
• синий C за пределами красного BC, но внутри двух других, так что дайте ему код 010.

Начиная с А:

• код ненулевой, не включайте синий A в вывод;
• если смотреть на ребро синего цвета AB, двоичное И ненулевое, поэтому не учитывайте вывод;
• код для синего B ненулевой, не включайте в вывод;
• коды B и C И до 0, так что XOR* им. Дает 110. Так что найдите пересечения синего BC с краями красного AB и BC, добавьте их в список outpyt;
• код для синего C ненулевой, не включайте в вывод;
• коды синего C и D снова указывают на пересечение с BC и AB, так что добавьте к выходу.

(* или ИЛИ их; мы установили, что они не имеют ничего общего, поэтому это не имеет значения - я думаю, что XOR немного более наглядно говорит, что вы ищете различия)

Answer 2

Здесь описаны два метода, эффективных для выпуклых многоугольников - алгоритм Хоуи и алгоритм О'Рурка.
(Я использовал О'Рурка для выпуклых четырехугольников)

Answer 3

Просто намеки на оптимизацию.

Полное обсуждение того, какие ребра пересекаются и какие вершины принадлежат окончательному контуру, зависит только от алгебраических областей треугольников, образованных вершиной одного треугольника (A) и ребром другого (B).

Есть 9 таких треугольников, следовательно, 9 областей и 9 знаков. В любом случае, у трех треугольников, построенных с одной и той же вершиной (A), есть области, которые суммируются с областью (B), и только 9 - 3 + 1 = 7 областей должны быть полностью вычислены.

Кроме того, точка пересечения между двумя ребрами вычисляется по двум областям, используя формулу типа t= S / (S - S'), где t - параметр вдоль ребра.

Таким образом, полностью развернутый алгоритм может быть записан в виде дерева решений глубиной 9 (с использованием 9 подписанных областей), причем каждый лист (512 из них!) Генерирует последовательность вершин / пересечений. В худшем случае может быть 6 перекрестков.