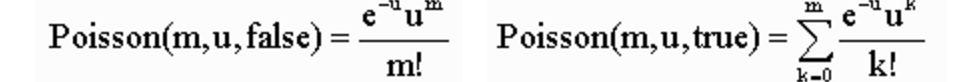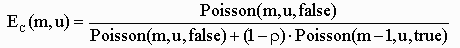Расчет Пуассона (эрланг С)

Question

Расчет Пуассона (эрланг С)

Я разместил это раньше, пользователь сказал мне, чтобы опубликовать это на codereview. я сделал, и они закрыли это... так еще раз здесь: (я удалил старый вопрос)

У меня есть эти формулы:

и мне нужны формулы Пуассона для формулы erlangC:

Я пытался перестроить формулы в C:

double getPoisson(double m, double u, bool cumu)
{
    double ret = 0;
    if(!cumu)
    {
        ret = (exp(-u)*pow(u,m)) / (factorial(m));
    }
    else
    {
        double facto = 1;
        double ehu = exp(-u);
        for(int i = 0; i < m; i++)
        {
            ret = ret + (ehu * pow(u,i)) / facto;
            facto *= (i+1);
        }
     }
     return ret;
}

Erlang C Формула:

double getErlangC(double m, double u, double p)
{
    double numerator = getPoisson(m, u, false);
    double denominator = getPoisson(m, u, false) + (1-p) * getPoisson(m, u, true);
    return numerator/denominator;
}

Основная проблема заключается в m параметр в getPoisson большое значение (>170), поэтому он хочет рассчитать>170! но он не может справиться с этим. Я думаю, что примитивные типы данных слишком малы, чтобы работать правильно, или что вы скажете?

Кстати: это факториальная функция, которую я использую для первого Пуассона:

double factorial(double n)
{
    if(n >= 1)
        return n*factorial(n-1);
    else
        return 1;
}

Некоторые образцы:

Входные данные:

double l = getErlangC(50, 48, 0.96);
printf("%g", l);

Выход:

0.694456 (correct)

Входные данные:

double l = getErlangC(100, 96, 0.96);
printf("%g", l);

Выход:

0.5872811 (correct)

если я использую значение выше 170 для первого параметра (m) getErlangC, например:

Входные данные:

double l = getErlangC(500, 487, 0.974);
printf("%g", l);

Выход:

naN (incorrect)

Освобожденные:

0.45269

Как мой подход? Будет ли лучший способ рассчитать Пуассона и ErlangC?

Некоторая информация: в Excel есть функция POISSON, а в Excel она работает идеально... будет ли способ увидеть алгоритм (код), который EXCEL использует для POISSON?

0

c poisson

Источник

user6727451 23 авг '16 в 20:32

3 ответа

Решение

Справиться со значениями, превышающими double диапазон, перекодировать, чтобы использовать журнал значений. Недостаток - некоторая потеря точности.

Точность может быть восстановлена с помощью улучшенного кода, но здесь есть кое-что, что по крайней мере справляется с проблемами диапазона.

Ниже приведен небольшой вариант кода ОП: используется для сравнения.

long double factorial(unsigned m) {
  long double f = 1.0;
  while (m > 0) {
    f *= m;
    m--;
  }
  return f;
}

double getPoisson(unsigned m, double u, bool cumu) {
  double ret = 0;
  if (!cumu) {
    ret = (double) ((exp(-u) * pow(u, m)) / (factorial(m)));
  } else {
    double facto = 1;
    double ehu = exp(-u);
    for (unsigned i = 0; i < m; i++) {
      ret = ret + (ehu * pow(u, i)) / facto;
      facto *= (i + 1);
    }
  }
  return ret;
}

double getErlang(unsigned m, double u, double p) {
  double numerator = getPoisson(m, u, false);
  double denominator = numerator + (1.0 - p) * getPoisson(m, u, true);
  return numerator / denominator;
}

Предлагаемые изменения

#ifdef M_PI
  #define  MY_PI M_PI
#else
  #define  MY_PI 3.1415926535897932384626433832795
#endif

// log of n!
//
// Gosper Approximation of Stirling's Approximation
// http://mathworld.wolfram.com/StirlingsApproximation.html
// n! about= sqrt(pi*(2*n + 1/3.)) * pow(n,n)  * exp(-n)
static double ln_factorial(unsigned n) {
  if (n <= 1) return 0.0;
  double x = n;
  return log(sqrt(MY_PI * (2 * x + 1 / 3.0))) + log(x) * x - x;
}


double getPoisson_2(unsigned m, double u, bool cumu) {
  double ret = 0.0;
  if (cumu) {
    // Simplify term calculation.  `mul` does not get too large nor small.
    double mul = exp(-u);
    for (unsigned i = 0; i < m; i++) {
      ret += mul;
      mul *= u/(i + 1);
      // printf("ret:% 10e  mul:% 10e\n", ret, mul);
    }
  } else {
    // ret = (exp(-u) * pow(u, m)) / (factorial(m));
    double ln_ret = -u + log(u) * m - ln_factorial(m);
    return exp(ln_ret);
  }
  return ret;
}

double getErlang_2(unsigned m, double u, double p) {
  double numerator = getPoisson_2(m, u, false);
  double denominator = numerator + (1 - p) * getPoisson_2(m, u, true);
  return numerator / denominator;
}

Тестовый код

void ErTest(unsigned m, double u, double p, double expect) {
  printf("m:%4u  u:% 14e  p:% 14e", m, u, p);
  printf("  E0:% 14e", expect);
  double y1 = getErlang(m, u, p);
  printf("  E1:% 14e", y1);
  double y2 = getErlang_2(m, u, p);
  printf("  E2:% 14e", y2);
  puts("");
}

int main(void) {
  ErTest(50, 48, 0.96, 0.694456);
  ErTest(100, 96, 0.96, 0.5872811);
  ErTest(500, 487, 0.974, 0.45269);
}

m:  50  u:  4.800000e+01  p:  9.600000e-01  E0:  6.944560e-01  E1:  6.944556e-01  E2:  6.944562e-01
m: 100  u:  9.600000e+01  p:  9.600000e-01  E0:  5.872811e-01  E1:  5.872811e-01  E2:  5.872813e-01
m: 500  u:  4.870000e+02  p:  9.740000e-01  E0:  4.526900e-01  E1:           nan  E2:  4.464746e-01

1

Источник

user2410359 23 авг '16 в 21:59

Ваш большой рекурсив factorial является проблемой, так как это может привести к переполнению стека, а также переполнению значения. pow может также стать большим.

Вот способ поэтапного объединения вещей:

double
getPoisson(double m, double u, bool cumu)
{
    double sum = 0;
    double facto = 1;
    double u_i = 1;
    double ehu = exp(-u);
    double cur = ehu;

    // u_i -- pow(u,i)
    // cur -- current/last term in series
    // sum -- sum of terms

    for (int i = 0; i < m; i++) {
        cur = (ehu * u_i) / facto;
        sum += cur;

        u_i *= u;
        facto *= (i + 1);
    }

    return cumu ? sum : cur;
}

Выше приведено "хорошо", но все же может переполнить некоторые значения из-за u_i а также facto термины.

Вот альтернатива, которая объединяет термины в виде отношения. Менее вероятно переполнение:

double
getPoisson(double m, double u, bool cumu)
{
    double sum = 0;
    double ehu = exp(-u);
    double cur = ehu;
    double ratio = 1;

    // cur -- current/last term in series
    // sum -- sum of terms
    // ratio -- u^i / factorial(i)

    for (int i = 0; i < m; i++) {
        cur = ehu * ratio;
        sum += cur;

        ratio *= u;
        ratio /= (i + 1);
    }

    return cumu ? sum : cur;
}

Выше может все еще привести к большим значениям. Если так, возможно, вам придется использовать long double, quadmathили многоточная арифметика. Или придумайте "аналог" уравнения / алгоритма.

0

Источник

user5382650 23 авг '16 в 22:01

Другие вопросы по тегам c poisson

user3169961 23 авг '16 в 21:15 2016-08-23 21:15 · Accepted Answer · 2016-08-23 21:15

(pow(u, m)/factorial(m)) может быть выражен как рекурсивный цикл с каждым элементом, показанным как u/n, где каждый n является элементом m!.

double ratio(double u, int n)
{
    if(n > 0)
     {
        // Avoid the ratio overflow by calculating each ratio element
        double val;
        val = u/n;
        return val*ratio(u, n-1);
      }
    else
      {
         // Avoid division by 0 as power and factorial of 0 are 1
        return 1;
      }
}

Обратите внимание, что если вы хотите избежать рекурсии, вы также можете сделать это как цикл

double ratio(double u, int n)
{
    int i;
    // Avoid the ratio overflow by calculating each ratio element
    // default the ratio to 1 for n == 0
    double val = 1;
    // calculate the next n-1 ratios and put them into the total
    for (i = 1; i<=n; i++)
      {
        // Put in the next element of the ratio 
        val *=  u/i;
      }
    // return the final value of the ratio
    return val;
}