Угол между двумя векторами в R
Какой самый эффективный способ в языке программирования R рассчитать угол между двумя векторами?
9 ответов
Согласно странице 5 этого PDF, sum(a*b) команда R, чтобы найти скалярное произведение векторов a а также b, а также sqrt(sum(a * a)) команда R для нахождения нормы вектора a, а также acos(x) является командой R для арккосинуса. Отсюда следует, что R-код для вычисления угла между двумя векторами
theta <- acos( sum(a*b) / ( sqrt(sum(a * a)) * sqrt(sum(b * b)) ) )
Мой ответ состоит из двух частей. Часть 1 является математикой - чтобы дать ясность всем читателям потока и сделать понятным следующий код R. Часть 2 - это программирование на R.
Часть 1 - Математика
Точечное произведение двух векторов x и y может быть определено как:
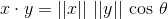
где || х || является евклидовой нормой (также известной как норма L 2) вектора x.
Манипулируя определением точечного произведения, мы можем получить:
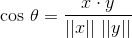
где тета - угол между векторами х и у, выраженный в радианах. Обратите внимание, что тета может принимать значение, лежащее на отрезке от 0 до pi.
Решая для самой тэты, мы получаем:
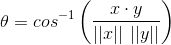
Часть 2 - код R
Чтобы перевести математику в код R, нам нужно знать, как выполнить два матричных (векторных) вычисления; скалярное произведение и евклидова норма (которая является специфическим типом нормы, известной как норма L 2). Нам также нужно знать R-эквивалент обратной косинус-функции, cos -1.
Начиная сверху. Ссылаясь на ?"%*%" точечное произведение (также называемое внутренним произведением) может быть вычислено с использованием %*% оператор. В отношении ?norm, norm() функция (базовый пакет) возвращает норму вектора. Здесь интересующей нормой является норма L 2 или, на языке справочной документации R, "спектральная" или "2"-норма. Это означает, что type аргумент norm() функция должна быть установлена равной "2", Наконец, обратная косинус-функция в R представлена acos() функция.
Решение
Оснащенная как математикой, так и соответствующими функциями R, можно создать функцию-прототип (то есть не производственный стандарт) - используя функции базового пакета - как показано ниже. Если приведенная выше информация имеет смысл, то angle() Следующая функция должна быть понятна без дальнейших комментариев.
angle <- function(x,y){
dot.prod <- x%*%y
norm.x <- norm(x,type="2")
norm.y <- norm(y,type="2")
theta <- acos(dot.prod / (norm.x * norm.y))
as.numeric(theta)
}
Проверьте функцию
Тест, чтобы убедиться, что функция работает. Пусть x = (2,1) и y = (1,2). Произведение точки между x и y равно 4. Евклидова норма x равна sqrt(5). Евклидова норма у также является квадратом (5). cos theta = 4/5. Тета составляет примерно 0,643 радиана.
x <- as.matrix(c(2,1))
y <- as.matrix(c(1,2))
angle(t(x),y) # Use of transpose to make vectors (matrices) conformable.
[1] 0.6435011
Надеюсь, это поможет!
Для 2D-векторов способ, указанный в принятом ответе и других, не учитывает ориентацию (знак) угла (angle(M,N) такой же как angle(N,M)) и возвращает правильное значение только для угла между 0 а также pi,
Использовать atan2 функция, чтобы получить ориентированный угол и правильное значение (по модулю 2pi).
angle <- function(M,N){
acos( sum(M*N) / ( sqrt(sum(M*M)) * sqrt(sum(N*N)) ) )
}
angle2 <- function(M,N){
atan2(N[2],N[1]) - atan2(M[2],M[1])
}
Проверь это angle2 дает правильное значение:
> theta <- seq(-2*pi, 2*pi, length.out=10)
> O <- c(1,0)
> test1 <- sapply(theta, function(theta) angle(M=O, N=c(cos(theta),sin(theta))))
> all.equal(test1 %% (2*pi), theta %% (2*pi))
[1] "Mean relative difference: 1"
> test2 <- sapply(theta, function(theta) angle2(M=O, N=c(cos(theta),sin(theta))))
> all.equal(test2 %% (2*pi), theta %% (2*pi))
[1] TRUE
Вы должны использовать точечный продукт. Скажем, у вас есть V₁ = (x₁, y₁, z₁) и V₂ = (x₂, y₂, z₂), тогда вычисляется скалярное произведение, которое я обозначу через V₁ ·V₂ как
V₁ ·V₂ = x₁ ·x₂ + y₁ ·y₂ + z₁ ·z₂ = |V₁ | · |V₂ | · Cos (θ);
Это означает, что сумма, показанная слева, равна произведению абсолютных значений векторов на косинус угла между векторами. абсолютное значение векторов V₁ и V calculated рассчитывается как
|V₁ | = √ (x₁² + y₁² + z₁²) и
|V₂ | = √ (x₂² + y₂² + z₂²),
Итак, если вы переставите первое уравнение выше, вы получите
cos (θ) = (x₁ ·x₂ + y₁ ·y₂ + z₁ ·z₂) ÷ (|V₁ | · |V₂ |),
и вам просто нужно, чтобы функция arccos (или обратный косинус) применялась к cos (θ), чтобы получить угол.
В зависимости от вашей функции arccos угол может быть в градусах или радианах.
(Для двухмерных векторов просто забудьте координаты z и выполните те же вычисления.)
Удачи,
Джон Донер
Другое решение: корреляция между двумя векторами равна косинусу угла между двумя векторами.
поэтому угол может быть вычислен acos(cor(u,v))
# example u(1,2,0) ; v(0,2,1)
cor(c(1,2),c(2,1))
theta = acos(cor(c(1,2),c(2,1)))
Если вы устанавливаете / загружаете библиотеку (matlib): есть функция под названием angle(x, y, deg = TRUE), где x и y - векторы. Примечание: если у вас есть x и y в матричной форме, используйте as.vector(x) и as.vector(y):
library(matlib)
matA <- matrix(c(3, 1), nrow = 2) ##column vectors
matB <- matrix(c(5, 5), nrow = 2)
angle(as.vector(matA), as.vector(matB))
##default in degrees, use degree = FALSE for radians
Традиционный подход к получению угла между двумя векторами (т.е.
acos(sum(a*b) / (sqrt(sum(a*a)) * sqrt(sum(b*b)))), как представлено в некоторых других ответах), страдает числовой нестабильностью в нескольких крайних случаях. Следующий код работает для n -размеров и во всех угловых случаях (он не проверяет векторы нулевой длины, но это легко добавить). См. примечания ниже.
# Get angle between two n-dimensional vectors
angle_btw <- function(v1, v2) {
signbit <- function(x) {
x < 0
}
u1 <- v1 / norm(v1, "2")
u2 <- v2 / norm(v2, "2")
y <- u1 - u2
x <- u1 + u2
a0 <- 2 * atan(norm(y, "2") / norm(x, "2"))
if (!(signbit(a0) || signbit(pi - a0))) {
a <- a0
} else if (signbit(a0)) {
a <- 0.0
} else {
a <- pi
}
a
}
Этот код адаптирован из реализации Julia Джеффри Сарноффа (лицензия MIT), в свою очередь, на основе этих заметок профессора В. Кахана (стр. 15).
Если вы хотите вычислить угол между несколькими переменными, вы можете использовать следующую функцию, которая является расширением решения, предоставленного @Graeme Walsh.
angles <- function(matrix){
## Calculate the cross-product of the matrix
cross.product <- t(matrix)%*%matrix
## the lower and the upper triangle of the cross-product is the dot products among vectors
dot.products<- cross.product[lower.tri(cross.product)]
## Calculate the L2 norms
temp <- suppressWarnings(diag(sqrt(cross.product)))
temp <- temp%*%t(temp)
L2.norms <- temp[lower.tri(temp)]
## Arccosine values for each pair of variables
lower.t <- acos(dot.products/L2.norms)
## Create an empty matrix to present the results
result.matrix <- matrix(NA,ncol = dim(matrix)[2],nrow=dim(matrix)[2])
## Fill the matrix with arccosine values and assign the diagonal values as zero “0”
result.matrix[lower.tri(result.matrix)] <- lower.t
diag(result.matrix) <- 0
result.matrix[upper.tri(result.matrix)] <- t(result.matrix)[upper.tri(t(result.matrix))]
## Get the result matrix
return(result.matrix)
}
Кроме того, если вы отцентрируете свои входные переменные по центру и получите значения косинуса результирующей матрицы, представленной выше, вы получите точную матрицу корреляции переменных.
Вот приложение функции.
set.seed(123)
n <- 100
m <- 5
# Generate a set of random variables
mt <- matrix(rnorm(n*m),nrow = n,ncol = m)
# Mean-centered matrix
mt.c <- scale(mt,scale = F)
# Cosine angles
cosine.angles <- angles(matrix = mt)
> cosine.angles
[,1] [,2] [,3] [,4] [,5]
[1,] 0.000000 1.630819 1.686037 1.618119 1.751859
[2,] 1.630819 0.000000 1.554695 1.523353 1.712214
[3,] 1.686037 1.554695 0.000000 1.619723 1.581786
[4,] 1.618119 1.523353 1.619723 0.000000 1.593681
[5,] 1.751859 1.712214 1.581786 1.593681 0.000000
# Centered-data cosine angles
centered.cosine.angles <- angles(matrix = mt.c)
> centered.cosine.angles
[,1] [,2] [,3] [,4] [,5]
[1,] 0.000000 1.620349 1.700334 1.614890 1.764721
[2,] 1.620349 0.000000 1.540213 1.526950 1.701793
[3,] 1.700334 1.540213 0.000000 1.615677 1.595647
[4,] 1.614890 1.526950 1.615677 0.000000 1.590057
[5,] 1.764721 1.701793 1.595647 1.590057 0.000000
# This will give you correlation matrix
cos(angles(matrix = mt.c))
[,1] [,2] [,3] [,4] [,5]
[1,] 1.00000000 -0.04953215 -0.12917601 -0.04407900 -0.19271110
[2,] -0.04953215 1.00000000 0.03057903 0.04383271 -0.13062219
[3,] -0.12917601 0.03057903 1.00000000 -0.04486571 -0.02484838
[4,] -0.04407900 0.04383271 -0.04486571 1.00000000 -0.01925986
[5,] -0.19271110 -0.13062219 -0.02484838 -0.01925986 1.00000000
# Orginal correlation matrix
cor(mt)
[,1] [,2] [,3] [,4] [,5]
[1,] 1.00000000 -0.04953215 -0.12917601 -0.04407900 -0.19271110
[2,] -0.04953215 1.00000000 0.03057903 0.04383271 -0.13062219
[3,] -0.12917601 0.03057903 1.00000000 -0.04486571 -0.02484838
[4,] -0.04407900 0.04383271 -0.04486571 1.00000000 -0.01925986
[5,] -0.19271110 -0.13062219 -0.02484838 -0.01925986 1.00000000
# Check whether they are equal
all.equal(cos(angles(matrix = mt.c)),cor(mt))
[1] TRUE
Я думаю, что вам нужен внутренний продукт. Для двух векторов v,u (в R^n или любые другие пространства внутреннего продукта) <v,u>/|v||u|= cos(alpha), (мы alpha это угол между векторами)
для более подробной информации смотрите: